决策树——信息熵,熵增益率,基尼系数的计算说明
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。
1. 信息增益 在 ID3 决策树中使用
”信息熵“是度量样本集合纯度最常用的指标,假设当前样本集合D中第k类样本所占比例为p_k(k=1,2,3,…,|y|),则D 的信息熵定义为:
E n t ( D ) = − ∑ k = 1 ∣ y ∣ ∗ p k l o g 2 p k Ent(D)=-\sum_{k=1}^{|y|}*p_klog_2p_k Ent(D)=−k=1∑∣y∣∗pklog2pk . Ent(D)的值越小,则D的纯度越高。
信息增益:
G a i n ( X , A ) = E n t ( X ) − E n t ( X ∣ A ) Gain(X,A) = Ent(X) - Ent(X|A) Gain(X,A)=Ent(X)−Ent(X∣A)
E n t ( X ∣ A ) = ∑ a ∈ A p ( a ) E n t ( X ∣ A = a ) Ent(X∣A)= \sum_{a∈A} p(a)Ent(X∣A=a) Ent(X∣A)=a∈A∑p(a)Ent(X∣A=a)
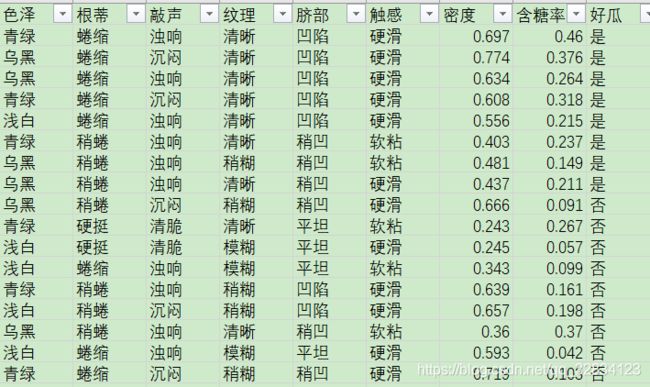
import pandas as pd
import math
df = pd.read_excel(r'c:/Users/Lenovo/Desktop/test3.xlsx')
"""
计算不同种类中不同类别的信息熵
"""
every_project_type_dict = {}
for i in df.columns[0:6]:
df_sel = df[[i, '好瓜']]
# 同一类别添加在一个字典中
every_dicr = {}
# 遍历每个类别,分别计算其占比情况,计算对应的熵值
for j in set(df_sel[i]):
y = df_sel[(df_sel[i] == j) & (df_sel['好瓜'] == '是')].shape[0]
x = df_sel[(df_sel[i] == j) & (df_sel['好瓜'] == '否')].shape[0]
rate_y = y / (x + y)
rate_x = x / (x + y)
"""
熵值公式:sum(-p_i*log2*(p_i))
"""
if rate_x == 0.0:
ent = -rate_y * math.log2(rate_y)
elif rate_y == 0.0:
ent = -rate_x * math.log2(rate_x)
elif rate_x != 0.0 and rate_y != 0.0:
ent = -rate_y * math.log2(rate_y) - rate_x * math.log2(rate_x)
print('大类:{},类别:{},熵值为:{}'.format(i, j, str(ent)))
every_dicr[j] = ent
every_project_type_dict[i] = every_dicr
## 计算每个类别不同种类的占比
type_rate_dict = {}
for i in df.columns[0:6]:
ssd_dict = {}
df_sel = df[[i]]
for j in set(df_sel[i]):
cnt = df_sel[df_sel[i] == j].count()
ssd_dict[j] = cnt[0] / df_sel.shape[0]
type_rate_dict[i] = ssd_dict
print(type_rate_dict)
# 好坏瓜的信息熵
y = df[df['好瓜'] == '是'].shape[0]
x = df[df['好瓜'] == '否'].shape[0]
rate_y = y / (x + y)
rate_x = x / (x + y)
b = -rate_y * math.log2(rate_y) - rate_x * math.log2(rate_x)
# 遍历每个大类
ent_num = {}
for s_keys in every_project_type_dict.keys():
ent_sum = 0
# 遍历每个小类别
for ss_keys in every_project_type_dict[s_keys]:
ss = every_project_type_dict[s_keys][ss_keys] * type_rate_dict[s_keys][ss_keys]
ent_sum += ss
ent = b - ent_sum
ent_num[s_keys] = ent
print(ent_num)
{'色泽': 0.10812516526536531, '根蒂': 0.14267495956679277, '敲声': 0.14078143361499584, '纹理': 0.3805918973682686, '脐部': 0.28915878284167895, '触感': 0.006046489176565584}
2. 增益率 在 C4.5 决策树中使用
G a i n r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} Gainratio(D,a)=IV(a)Gain(D,a)
其中,
I V ( a ) = − ∑ v = 1 v ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^{v}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(a)=−v=1∑v∣D∣∣Dv∣log2∣D∣∣Dv∣
其中,a的取值数目越多(即V越大),则IV(a)的值通常会越大。
### IV 值
IV_dict = {}
for key in type_rate_dict.keys():
ent_ = 0
for valus in type_rate_dict[key].values():
ent_sum = -valus * math.log2(valus)
ent_ += ent_sum
IV_dict[key] = ent_
print(IV_dict)
# 信息熵增益率
ent_num_rate = {}
for s_keys in ent_num.keys():
ss = ent_num[s_keys] / IV_dict[s_keys]
ent_num_rate[s_keys] = ss
print(ent_num_rate)
{'色泽': 0.06843956584615815, '根蒂': 0.10175939805373684, '敲声': 0.10562670944314426, '纹理': 0.2630853587192754, '脐部': 0.1867268991844879, '触感': 0.0069183298534003}
3. 基尼系数在 CART 决策树中使用
Gini越小,数据集D的纯度越高。表示方法如下:
G i n i ( D ) = 1 − ∑ k = 1 ∣ y ∣ p k 2 Gini(D)=1-\sum_{k=1}^{|y|}p_k^2 Gini(D)=1−k=1∑∣y∣pk2
属性a的基尼指数定义为:
G i n i i n d e x ( D , a ) = ∑ v = 1 v G i n i ( D v ) Gini_index(D,a)=\sum_{v=1}^{v}Gini(D^v) Giniindex(D,a)=v=1∑vGini(Dv)
## 每一项目中 不同类别的基尼系数
every_project_type_dict = {}
for i in df.columns[0:6]:
df_sel = df[[i, '好瓜']]
every_type_dict = {}
for j in set(df_sel[i]):
y = df_sel[(df_sel[i] == j) & (df_sel['好瓜'] == '是')].shape[0]
x = df_sel[(df_sel[i] == j) & (df_sel['好瓜'] == '否')].shape[0]
rate_y = y / (x + y)
rate_x = x / (x + y)
gini = 1 - rate_x ** 2 - rate_y ** 2
print('项目:{},类别:{},基尼系数:{}'.format(i, j, str(gini)))
every_type_dict[j] = gini
every_project_type_dict[i] = every_type_dict
every_project_type_dict
### 整体类别的基尼系数
every_pro_num = {}
for keys in every_project_type_dict.keys():
gini = 0
for ss_keys in every_project_type_dict[keys].keys():
ss = every_project_type_dict[keys][ss_keys] * type_rate_dict[keys][ss_keys]
gini += ss
every_pro_num[keys] = gini
print(every_pro_num)
{'色泽': 0.42745098039215684, '根蒂': 0.42226890756302526, '敲声': 0.4235294117647059, '纹理': 0.2771241830065359, '脐部': 0.3445378151260504, '触感': 0.49411764705882355}