从行、列向量与坐标转换矩阵说起

先从二维坐标转换说起：

一：矩阵和行、列向量

1.        二维坐标R2中原始自然基e[1,0; 0,1]，坐标变换矩阵M1 = [cost, -sint; sint , cost];  t代表向左旋转的角度为正，向右旋转为负；对应变换的向量应该为列向量A[1; 1]， 并且变换后得到的向量B = M1 * A = [cost, -sint; sint, cost  ] [1; 1] = [cost - sint ; sint + cost ]；

2.        二维坐标R2中原始自然基e[1,0; 0,1]，坐标变换矩阵M2 = M1^T = M1的转置 = [cost, sint; -sint , cost];  t代表向左旋转的角度为正，向右旋转为负；对应变换的向量应该为行向量A[1， 1]， 并且变换后得到的向量B = A * M1  = [1,1] [cost, sint; -sint, cost  ]  = [cost - sint , sint + cost ]；

3.        代数方面的理解 B = M1 * A; B^T = (M1*A)^T = A^T * M1^T;

4.        注意这里的B的坐标的基还是自然基e[1.0; 0,1];

二：基变换的过渡矩阵

1.        接着一中的矩阵M1再讨论：把坐标变换矩阵M1看成是一个基[cost, -sint; sint , cost]， 那么由向量空间R2中的自然基e[1, 0;  0, 1]变换到基M1，e * M = M1;  M = M1;

2.       那么R2下，两个非自然基： M = [m1,m2];  m1 = [1;1] , m2=[2; 0]; M = [1 , 2; 1, 0];   

        N = [n1,n2]  ; n1 = [-1;1]; n2 = [1;1];  N = [-1,1; 1,1]; 如果想通过一个矩阵P, 把基m1,m2,变换到基n1,n2; 那么P？ 由1得到:基M到基e，M->e =  M^-1；基e到基n即为n；所以 P = M^-1 * N;

3.        注意上面的1，2是在矩阵有逆的情况话，也即矩阵必须是方阵并且行列式不能是0，如果基M不是方阵。 如果P= [p11, p12; p21, p22], 那么(n1,n2) = (m1,m2) * P ->   n1 =  m1 * p11 + m2 * p21;  n2  = m1*p12 + m2*p22;  从中可以看出，向量n1, n2, 在基m1，m2张成空间中，才有解，也即n1,n2是m1,m2的线性组合；

4.        所以已知两个基m1,m2,...,ms;  n1,n2,...,ns, 当且仅当它们是同一个向量空间的基是，才有n1,n2,...,ns = (m1,m2,..,ms )* P, 由基M变换到基N的基变换矩阵P就是过渡矩阵。

三：基于基变换的坐标变换

1.        由二得到基M到N的过渡矩阵P， n1..ns = (m1..ms)P,    P = M^-1 * N;  那么 已知基e下向量xe = [-2.-2], 非自然基M = [1, 2; 1,0];那么基xe下的坐标到基M下的坐标xm？ 因为二维空间中向量不变，xe和xm是不同基的不同表达，但是向量x在二维空间中没有变化， 所以-2e1 - 2e2 = x = mx1 * m1+ mx2 * m2;  也即( -2；-2 ）=  (m1,m2)*(mx1; mx2);   xe = M(mx); 所以 mx = M^-1*xe;

那么已知两个基m1,m2,...,ms;  n1,n2,...,ns, 当且仅当它们是同一个向量空间的基是，才有n1,n2,...,ns = (m1,m2,..,ms )* P, 由基M变换到基N的基变换矩阵P就是过渡矩阵， 又知道向量x在基M的坐标Xm， 基N下的坐标Xn， 那么 Xn = P^-1 * Xm; Xm = P * Xn;

四：由基的坐标变换到相似矩阵、等价矩阵

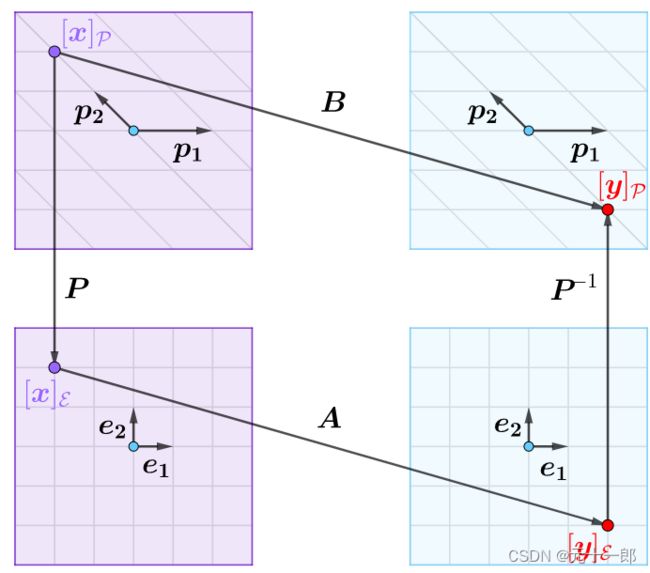
1.        相似矩阵其实是同一线性映射在不同基的代数表示。 B矩阵是基N下向量的变换或者说是映射， A矩阵是基M下向量的变换或者说是映射。那么比如N下的一个向量Xn 经过B变换称为Yn； 可以把N下的Xn先做基变换矩阵P=N^-1*M，变成M基下的Xm，经过矩阵A变换Xm称为基M下的向量Ym；最后再通过P^-1，变换M基下的Ym到N基下的Yn；所以得到线性映射矩阵 B = P ^-1 * A * P； A和B相似，都代表不同基下的同一种线性映射。

        定义： 设A，B都是n阶方阵，若有可逆矩阵P，使得B = P^-1 * A * P, 则P为相似变换矩阵， B是A的相似矩阵；下图片由马同学提供。帮助理解。

等价矩阵和相似矩阵类似， 形如：C = QAP， P为基变换， A为和C的一样的变换，Q为基的逆变换，称A和C为等价矩阵。

五：矩阵的幂(A^n)计算：特征值和特征向量和相似矩阵得到对角矩阵

1. 矩阵完成的是一个向量空间到另外一个向量空间的映射，非零向量x1经过矩阵A, 得到x2 = A*x1; x2可能发生向量的大小和方向的变化，其中x2中的方向和x1方向在一条直线的变化,说明向量x1经过矩阵A发生了拉伸的变化，那么这样的向量就称为矩阵A的特征向量，大小的变化 称为矩阵A的特征向量对应的特征值。A * x =  * x ; 

        假设 A = [ cost, -sint; sint, cost  ]; 到t = 45度时， 该矩阵把所有x1向量都逆时针旋转了45度得到x2， 那么A没有特征向量及其对应的特征向量； 如果t = 180度时，改矩阵把所有向量x1都逆时针旋转了180度得到x2， 那么A就有特征向量及其对应的特征值-1, 所有向量拉伸-1倍。

    重要性质: 矩阵A的不同的特征值对应的特征向量，相互线性无关；因为线性无关，可以组成一组基。因为是一组基，所以可以形成过渡矩阵，进而得到A用对角矩阵和该组基表示，进而求出A的n次幂。

        假设A = [0.95, 0.03  ; 0.05, 0.97  ] ; 求得特征值和特征向量 r1 = 1; r2 = 0.92; p1 = [3,5]; p2 = [1,-1];  因为r1 != r2, 所以p1和p2线性无关，所以可以组成一组基， 所以基e到基p的过渡矩阵P = [p1, p2];  那么 AP = A(p1,p2) = (A*p1,  A*p2); 因为 p1和p2是A的特征向量，所以A*p1 = r1*p1; A*p2 = r2 * p2; 所以 AP = (r1 * p1, r2 *p2 ) = (r1 ,0 ; 0 ,r2) *(p1,p2) ; A = P^-1 * (r1 ,0 ; 0 ,r2) * P;

因为P^-1 * P = E; 所以 A^n = （P^-1 * 对角矩阵r *P ）（P^-1 * 对角矩阵r *P）。。。。（P^-1 * 对角矩阵r *P） = P^-1 * （对角矩阵r)^n  *P  = P^-1 * （r1^n,0; 0, r2^n)  *P;这里如果P是正交基，那么P^-1就是P^T. 可以大大简化计算。

六: 重要性质：若r1,r2...rn是n阶方阵A的特征值，那么|A| = r1 * r2 * ...*rn;  |A| != 0 那么ri != 0, 所以A可逆。

七: 迹和相似矩阵

        1.    迹：对于n阶方阵，其主对角线上的元素之和称为迹， tr(A) = a11+a22+...+ann; 

        2.    若r1,r2...rn是n阶方阵A的特征值，那么tr(A ) = r1+r2+...+rn;

       3.     若A和B相似，那么tr(A) = tr(B);

八：二次型函数和二次型矩阵

        1. 一些变量的二次齐次多项式被称为二次型, 如果其中包含了非二次项，就不是二次型;比如包含二次型的函数z = 3x1^2 + 5x2^2 + 4x1*x2

        2. 二次型矩阵, 如 z = 3x1^2 + 5x2^2 + 4x1*x2 = (x1 , x2) [3, 2; 2, 5] (x1; x2), 其中矩阵[3,2;2,5]作为二次型函数的矩阵，简称为二次型矩阵。可以简写函数 z = x^T * A * x

九：合同矩阵

        1.由二次型函数和二次型矩阵把椭圆函数：ax1^2 + 2bx1*x2+cx2^2 = 1 = x^T*A*x = 1, 那么假设椭圆在基p下的方程 xp^T * B * xp = 1, 假设P是基e到基p的过渡矩阵；

 假设B = P^T * A * P， 那么在基p下的椭圆方程 xp^T * B * xp = 1,  如果A是对称矩阵， 那么B也是对称矩阵。