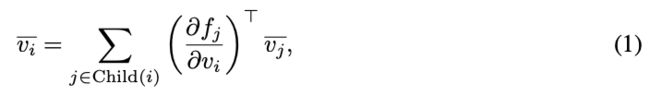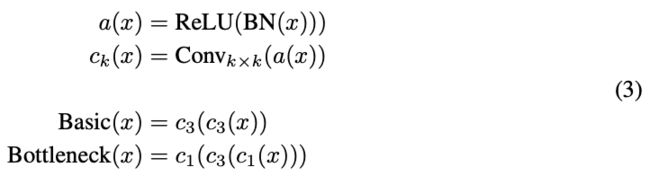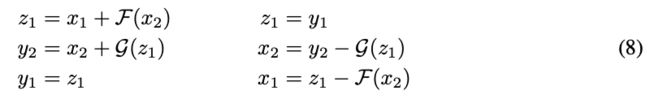可逆残差网络:不存储激活的反向传播 Reversible Residual Network: Backpropagation Without Storing Activations

The Reversible Residual Network: Backpropagation Without Storing Activations

[pdf]

Code available at GitHub - renmengye/revnet-public: Code for "The Reversible Residual Network: Backpropagation Without Storing Activations"

目录

Abstract

Introduction

Background

Methods

---

Abstract

Deep residual networks (ResNets) have significantly pushed forward the state-of-the-art on image classification, increasing in performance as networks grow both deeper and wider. However, memory consumption becomes a bottleneck, as one needs to store the activations in order to calculate gradients using backpropagation.

We present the Reversible Residual Network (RevNet), a variant of ResNets where each layer’s activations can be reconstructed exactly from the next layer’s. Therefore, the activations for most layers need not be stored in memory during backpropagation.

We demonstrate the effectiveness of RevNets on CIFAR-10, CIFAR-100, and ImageNet, establishing nearly identical classification accuracy to equally-sized ResNets, even though the activation storage requirements are independent of depth. 

深度残差网络 (ResNets) 极大地推动了图像分类的发展，随着网络的深度和广度的增长，性能也不断提高。然而，内存消耗成为一个瓶颈，因为需要存储激活以便使用反向传播计算梯度。

本文提出了可逆残差网络 (RevNet)，其中每一层的激活都可以精确地从下一层的激活重建。因此，在反向传播期间，大多数层的激活不需要存储在内存中。

在 CIFAR-10、CIFAR-100 和 ImageNet 上证明了 RevNets 的有效性，尽管激活存储要求与深度无关，但它们建立了与同等大小的 ResNets 几乎相同的分类精度。

Introduction

Over the last five years, deep convolutional neural networks have enabled rapid performance improvements across a wide range of visual processing tasks [19, 26, 20]. For the most part, the state-of-the-art networks have been growing deeper. For instance, deep residual networks (ResNets) [13] are the state-of-the-art architecture across multiple computer vision tasks [19, 26, 20]. The key architectural innovation behind ResNets was the residual block, which allows information to be passed directly through, making the backpropagated error signals less prone to exploding or vanishing. This made it possible to train networks with hundreds of layers, and this vastly increased depth led to significant performance gains.

在过去的五年中，深度卷积神经网络在广泛的视觉处理任务中实现了快速性能改进。在大多数情况下，最先进的网络正在不断深化。例如，深度残差网络 (ResNets) 是多个计算机视觉任务的最先进的架构。ResNets 背后的关键架构创新是 residual block，其允许信息直接通过，使反向传播的错误信号不容易爆炸或消失。这使得训练具有数百层的网络成为可能，这极大地增加了深度，从而显著提高了性能。

Nearly all modern neural networks are trained using backpropagation. Since backpropagation requires storing the network’s activations in memory, the memory cost is proportional to the number of units in the network. Unfortunately, this means that as networks grow wider and deeper, storing the activations imposes an increasing memory burden, which has become a bottleneck for many applications [34, 37]. Graphics processing units (GPUs) have limited memory capacity, leading to constraints often exceeded by state-of-the-art architectures, some of which reach over one thousand layers [13]. Training large networks may require parallelization across multiple GPUs [7, 28], which is both expensive and complicated to implement. Due to memory constraints, modern architectures are often trained with a mini-batch size of 1 (e.g. [34, 37]), which is inefficient for stochastic gradient methods [11]. Reducing the memory cost of storing activations would significantly improve our ability to efficiently train wider and deeper networks.

几乎所有的现代神经网络都是用反向传播训练的。由于反向传播需要将网络的激活存储在内存中，因此内存成本与网络中的单元数成正比。不幸的是，这意味着随着网络的扩大和深化，存储激活会增加内存负担，这已经成为许多应用程序的瓶颈。图形处理单元 (gpu) 内存容量是有限的，这导致了 state-of-the-art 架构经常超过的限制，有些甚至超过了1000层。训练大型网络可能需要跨多个gpu 的并行化，这既昂贵又复杂。由于内存的限制，现代架构通常使用 batch size 为 1 进行训练，这对于随机梯度方法是低效的。降低储存激活的记忆成本将显著提高我们有效训练更广更深网络的能力。

We present Reversible Residual Networks (RevNets), a variant of ResNets which is reversible in the sense that each layer’s activations can be computed from the subsequent reversible layer’s activations. This enables us to perform backpropagation without storing the activations in memory, with the exception of a handful of non-reversible layers. The result is a network architecture whose activation storage requirements are independent of depth, and typically at least an order of magnitude smaller compared with equally sized ResNets. Surprisingly, constraining the architecture to be reversible incurs no noticeable loss in performance: in our experiments, RevNets achieved nearly identical classification accuracy to standard ResNets on CIFAR-10, CIFAR-100, and ImageNet, with only a modest increase in the training time.

本文提出了可逆残差网络 (RevNets)，它是可逆的，因为每一层的激活都可以从后续可逆层的激活计算出来。其能够在不将激活存储在内存中 (少数不可逆层除外) 的情况下执行反向传播。其激活存储需求与深度无关，通常至少比同等大小的 ResNets 小一个数量级。将体系结构限制为可逆不会对性能造成明显的损失。实验中，RevNets 在 CIFAR-10、CIFAR-100 和 ImageNet 上实现了与标准 ResNets 几乎相同的分类精度，只是稍微增加了训练时间。

Background

Backpropagation

We treat backprop as an instance of reverse mode automatic differentiation [24]. Let v1, . . . , vK denote a topological ordering of the nodes in the network’s computation graph G, where vK denotes the cost function C. Each node is defined as a function fi of its parents in G. Backprop computes the total derivative dC/dvi for each node in the computation graph. This total derivative defines the the effect on C of an infinitesimal change to vi , taking into account the indirect effects through the descendants of vk in the computation graph. Note that the total derivative is distinct from the partial derivative ∂f /∂xi of a function f with respect to one of its arguments xi , which does not take into account the effect of changes to xi on the other arguments. To avoid using a small typographical difference to represent a significant conceptual difference, we will denote total derivatives using vi = dC/dvi.

这段基本就是反向传播中的字符定义：

我们将 backprop 作为反向模式 automatic differentiation 的一个实例。令 v1，…， vK 表示网络计算图 G 中节点的拓扑顺序，其中 vK 表示代价函数 C。每个节点定义为 G 中其父节点的函数 fi。Backprop 计算计算图中每个节点的总导数 dC/dvi。这个总导数定义了 vi 的无穷小变化对 C 的影响，并考虑了计算图中 vk 的后代对 C 的间接影响。请注意，总的导数不同于函数 f 对其一个参数的 ∂f /∂xi 的偏导数，它不考虑对其他参数的变化的影响。为了避免用一个小小的字体差异来表示一个显著的概念差异，我们将用 vi = dC/dvi 来表示总的导数。

Backprop iterates over the nodes in the computation graph in reverse topological order. For each node vi , it computes the total derivative vi using the following rule:

where Child(i) denotes the children of node vi in G and ∂fj/∂vi denotes the Jacobian matrix.

Backprop 以反向拓扑顺序迭代计算图中的节点。对于每个节点 vi，使用 (1) 计算总导数 vi。

其中 Child(i) 表示 G 中节点 vi 的子节点，∂fj/∂vi 表示雅可比矩阵。

Deep Residual Networks

One of the main difficulties in training very deep networks is the problem of exploding and vanishing gradients, first observed in the context of recurrent neural networks [3]. In particular, because a deep network is a composition of many nonlinear functions, the dependencies across distant layers can be highly complex, making the gradient computations unstable. Highway networks [29] circumvented this problem by introducing skip connections. Similarly, deep residual networks (ResNets) [13] use a functional form which allows information to pass directly through the network, thereby keeping the computations stable. ResNets currently represent the state-of-the-art in object recognition [13], semantic segmentation [35] and image generation [32]. Outside of vision, residuals have displayed impressive performance in audio generation [31] and neural machine translation [16].

训练深度网络的主要困难之一是梯度的爆炸和消失问题，这首先是在递归神经网络的背景下观察到的。特别是，由于深度网络是由许多非线性函数组成的，跨远层的依赖关系可能非常复杂，使得梯度计算不稳定。Highway 网通过引入跳跃连接来解决这个问题。类似地，深度残差网络 (ResNets)使用函数形式，允许信息直接通过网络，从而保持计算的稳定。

ResNets are built out of modules called residual blocks, which have the following form:

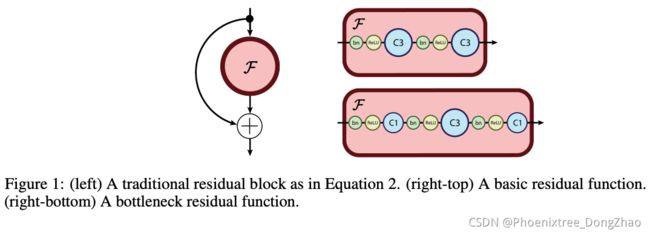
where F, a function called the residual function, is typically a shallow neural net. ResNets are robust to exploding and vanishing gradients because each residual block is able to pass signals directly through, allowing the signals to be propagated faithfully across many layers. As displayed in Figure 1, residual functions for image recognition generally consist of stacked batch normalization ("BN") [14], rectified linear activation ("ReLU") [23] and convolution layers (with filters of shape three "C3" and one "C1").

ResNets 介绍，可以略过。残余块的模块构建形式如 (2)。

其中 F为残差函数，是一个典型的浅的神经网络。ResNets 对于爆炸和消失的梯度非常 robust，因为每个残余块都能够直接传递信号，允许信号在许多层上直接传播。如图 1 所示，用于图像识别的残差函数一般由堆叠批处理归一化 (“BN”)、整流线性激活 (“ReLU”) 和卷积层 (形状为三个 “C3” 和一个“C1”的滤波器) 组成。
 

As in He et al. [13], we use two residual block architectures: the basic residual function (Figure 1 right-top) and the bottleneck residual function (Figure 1 right-bottom). The bottleneck residual consists of three convolutions, the first is a point-wise convolution which reduces the dimensionality of the feature dimension, the second is a standard convolution with filter size 3, and the final point-wise convolution projects into the desired output feature depth.

ResNet block 的基本构成结构，(3) 式已经一目了然了，可以略过。

在何凯明的 ResNet 中，使用了两个残余块架构:基本残余函数 (图 1 右上) 和瓶颈残余函数 (图 1 右下)。瓶颈残差由三个卷积组成，第一个是逐点卷积，降低特征维数的维数，第二个是滤子大小为 3 的标准卷积，最后的逐点卷积投射到期望的输出特征深度。 

Reversible Architectures

Various reversible neural net architectures have been proposed, though for motivations distinct from our own. Deco and Brauer [8] develop a similar reversible architecture to ensure the preservation of information in unsupervised learning contexts. The proposed architecture is indeed residual and constructed to produce a lower triangular Jacobian matrix with ones along the diagonal. In Deco and Brauer [8], the residual connections are composed of all ‘prior’ neurons in the layer, while NICE and our own architecture segments a layer into pairs of neurons and additively connect one with a residual function of the other. Maclaurin et al. [21] made use of the reversible nature of stochastic gradient descent to tune hyperparameters via gradient descent. Our proposed method is inspired by nonlinear independent components estimation (NICE) [9, 10], an approach to unsupervised generative modeling. NICE is based on learning a non-linear bijective transformation between the data space and a latent space. The architecture is composed of a series of blocks defined as follows, where x1 and x2 are a partition of the units in each layer:

各种可逆的神经网络结构已经被提出，尽管动机不同于本文。Deco 和 Brauer 开发了一个类似的可逆结构，以确保在无监督学习环境中信息的保存。所提出的结构确实是残差的，并且构造成一个沿对角线为 1 的下三角雅可比矩阵。在 Deco 和 Brauer 的工作中，残差连接由层中的所有“先验”神经元组成，而 NICE 和本文的结构将层分割成一对对神经元，并将其中一个与另一个的残差功能相加连接。Maclaurin 等人利用随机梯度下降的可逆性质，通过梯度下降来调整超参数。我们提出的方法是受非线性独立分量估计 (NICE) 的启发，NICE 是一种无监督生成建模方法。NICE 是基于学习数据空间和潜在空间之间的非线性双目标转换。该体系结构由一系列定义 (4) 的块组成，其中x1 和 x2 是每一层单元的划分。

Because the model is invertible and its Jacobian has unit determinant, the log-likelihood and its gradients can be tractably computed. This architecture imposes some constraints on the functions the network can represent; for instance, it can only represent volume-preserving mappings. Follow-up work by Dinh et al. [10] addressed this limitation by introducing a new reversible transformation:

Here, represents the Hadamard or element-wise product. This transformation has a non-unit Jacobian determinant due to multiplication by exp (F(x1)).

由于该模型是可逆的，其雅可比矩阵具有单位行列式，因此对数似然及其梯度可以很容易地计算出来。这种结构对网络所能表示的功能施加了一些约束；例如，它只能表示保留卷的映射。Dinh 等人的后续工作通过引入一种新的可逆转变来解决这一限制，公式 (5)。

由于乘以 exp (F(x1))，这个变换有一个非单位的雅可比行列式。

Methods

We now introduce Reversible Residual Networks (RevNets), a variant of Residual Networks which is reversible in the sense that each layer’s activations can be computed from the next layer’s activations. We discuss how to reconstruct the activations online during backprop, eliminating the need to store the activations in memory.

我们现在介绍可逆残差网络 (RevNets)，它是可逆的，因为每一层的激活都可以从下一层的激活计算出来。我们讨论了如何在 backprop 过程中在线重建激活，消除了在内存中存储激活的需要。

Reversible Residual Networks

RevNets are composed of a series of reversible blocks, which we now define. We must partition the units in each layer into two groups, denoted x1 and x2; for the remainder of the paper, we assume this is done by partitioning the channels, since we found this to work the best in our experiments. Each reversible block takes inputs (x1, x2) and produces outputs (y1, y2) according to the following additive coupling rules – inspired by NICE’s [9] transformation in Equation 4 – and residual functions F and G analogous to those in standard ResNets:

RevNets 由一系列可逆块组成。将每一层的单元划分为两组，分别表示 x1 和 x2 ；对于本文的其余部分，我们假设这是通过划分信道来完成的，因为我们发现这在我们的实验中是最好的。每个可逆块接受输入 (x1, x2)，并根据以下相加耦合规则产生输出 (y1, y2) ——灵感来自方程 (4) 中的NICE 变换 —— 以及类似于标准 ResNets 中的残差函数 F 和 G，见公式 (6)。

Each layer’s activations can be reconstructed from the next layer’s activations as follows:

Note that unlike residual blocks, reversible blocks must have a stride of 1 because otherwise the layer discards information, and therefore cannot be reversible. Standard ResNet architectures typically have a handful of layers with a larger stride. If we define a RevNet architecture analogously, the activations must be stored explicitly for all non-reversible layers.

每一层的激活可以由下一层的激活重构为公式 (7)。

注意，与剩差块不同的是，可逆块中的跳接必须步幅为 1，否则该层将丢弃信息且不再可逆。标准的ResNet 架构通常有几个跨大的层。如果我们以类似的方式定义 RevNet 架构，则必须显式地存储所有不可逆层的激活。

Backpropagation Without Storing Activations

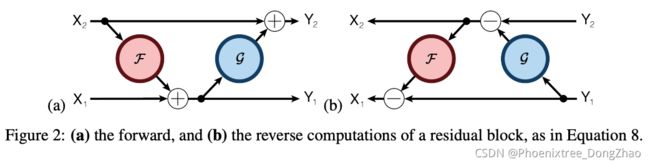
To derive the backprop procedure, it is helpful to rewrite the forward (left) and reverse (right) computations in the following way:

为了推导 backprop 过程，将正向 (左) 和反向 (右) 的计算重写为 (8)。

Even though z1 = y1, the two variables represent distinct nodes of the computation graph, so the total derivatives and are different. In particular,  includes the indirect effect through y2, while  does not. This splitting lets us implement the forward and backward passes for reversible blocks in a modular fashion. In the backwards pass, we are given the activations (y1, y2) and their total derivatives  (, ) and wish to compute the inputs (x1, x2), their total derivatives (, ), and the total derivatives for any parameters associated with F and G. (See Section 2.1 for our backprop notation.) We do this by combining the reconstruction formulas (Eqn. 8) with the backprop rule (Eqn. 1). The resulting algorithm is given as Algorithm 1. 

即使 z1 = y1，这两个变量代表了计算图上不同的节点，所以  和 的总导数是不同的。特别地， 包含了通过 y2 的间接效应，而 不包含。这种分割让我们能够以模块化的方式实现可逆块的前向和后向传递。在向后传递中，我们给出了激活 (y1, y2) 和它们的总导数 (, )，并希望计算输入 (x1, x2)，它们的总导数 (, )，以及与 F 和 G 相关的任何参数的总导数 (参见2.1节中的 backprop 符号)。我们将重建公式 (Eqn. 8) 与反向传播规则 (Eqn. 1) 相结合，得到的算法给出了算法 1.

By applying Algorithm 1 repeatedly, one can perform backprop on a sequence of reversible blocks if one is given simply the activations and their derivatives for the top layer in the sequence. In general, a practical architecture would likely also include non-reversible layers, such as subsampling layers; the inputs to these layers would need to be stored explicitly during backprop. However, a typical ResNet architecture involves long sequences of residual blocks and only a handful of subsampling layers; if we mirror the architecture of a ResNet, there would be only a handful of non-reversible layers, and the number would not grow with the depth of the network. In this case, the storage cost of the activations would be small, and independent of the depth of the network.

通过重复应用算法 1，只要简单地给出序列中顶层的激活及其衍生物，就可以在可逆块序列上执行 反向传播。一般来说，一个实用的体系结构可能还包括不可逆层，比如子采样层；在 backprop 过程中，需要显式存储这些层的输入。然而，一个典型的 ResNet 架构涉及长序列的残留块和只有少数子采样层；如果我们镜像一个 ResNet 的架构，那么就只有少数几个不可逆层，而且数量也不会随着网络深度的增加而增加。在这种情况下，激活的存储成本很小，而且与网络的深度无关。

Computational overhead

In general, for a network with N connections, the forward and backward passes of backprop require approximately N and 2N add-multiply operations, respectively. For a RevNet, the residual functions each must be recomputed during the backward pass. Therefore, the number of operations required for reversible backprop is approximately 4N, or roughly 33% more than ordinary backprop. (This is the same as the overhead introduced by checkpointing [22].) In practice, we have found the forward and backward passes to be about equally expensive on GPU architectures; if this is the case, then the computational overhead of RevNets is closer to 50%.

计算开销：一般来说，对于一个有 N 个连接的网络，backprop 的向前和向后传递分别需要大约 N个和 2N 个加乘操作。对于 RevNet，每个残差函数都必须在向后传递期间重新计算。因此，可逆反向传播所需的操作次数约为 4N，比普通反向传播多约 33%。(这与 checkpointing [22] 带来的开销相同。) 在实践中，我们发现向前和向后传递在 GPU 架构上的成本差不多；如果是这样，那么RevNets 的计算开销接近 50%。

Modularity

Note that Algorithm 1 is agnostic to the form of the residual functions F and G. The steps which use the Jacobians of these functions are implemented in terms of ordinary backprop, which can be achieved by calling automatic differentiation routines (e.g. tf.gradients or Theano.grad). Therefore, even though implementing our algorithm requires some amount of manual implementation of backprop, one does not need to modify the implementation in order to change the residual functions.

模块化：注意，算法 1 不知道残差函数 F 和 G 的形式。使用这些函数的雅可比矩阵的步骤是用普通的 backprop 来实现的，可以通过调用自动微分例程 (例如 tf.gradients 或 Theano.grad) 来实现。因此，即使实现我们的算法需要一些 backprop 的手动实现，也不需要修改实现来改变残差函数。

Numerical error

While Eqn. 8 reconstructs the activations exactly when done in exact arithmetic, practical float32 implementations may accumulate numerical error during backprop. We study the effect of numerical error in Section 5.2; while the error is noticeable in our experiments, it does not significantly affect final performance. We note that if numerical error becomes a significant issue, one could use fixed-point arithmetic on the x’s and y’s (but ordinary floating point to compute F and G), analogously to [21]. In principle, this would enable exact reconstruction while introducing little overhead, since the computation of the residual functions and their derivatives (which dominate the computational cost) would be unchanged.

数值误差：当 Eqn. 8 在精确的算术中精确地重建激活时，实际的 float32 实现可能会在 backprop 期间积累数值误差。在第 5.2 节中我们研究了数值误差的影响；虽然这个误差在我们的实验中很明显，但它并不会对最终的性能产生显著的影响。我们注意到，如果数值错误成为一个重要问题，可以对 x 和 y 使用定点算术 (但使用普通浮点来计算 F 和 G)，类似于[21]。原则上，这将使精确重建成为可能，同时引入很小的开销，因为残差函数及其导数的计算 (占计算成本的主要部分) 将保持不变。

下面是 5.2 节中的相关实验结果：

Impact of numerical error. As described in Section 3.2, reconstructing the activations over many layers causes numerical errors to accumulate. In order to measure the magnitude of this effect, we computed the angle between the gradients computed using stored and reconstructed activations over the course of training. Figure 4 shows how this angle evolved over the course of training for a CIFAR-10 RevNet; while the angle increased during training, it remained small in magnitude.

数值误差的影响。如上节所述，在多个层上重建激活会导致数值误差的累积。为了测量这种效应的大小，我们计算了在训练过程中使用存储和重建激活计算的梯度之间的角度。图 4 显示了这个角度在 CIFAR-10 RevNet 训练过程中是如何演变的；虽然这个角度在训练过程中增加了，但它的大小仍然很小。