【台大林轩田《机器学习基石》笔记】Lecture 7——The VC Dimension

Lecture 7:The VC Dimension

Definition of VC Dimension

定义：VC Dimension$d_{vc}=k-1$,其中k是之前提到的break point

也就是指假设集合$\mathcal{H}$最大能够shatter的点的个数

再来回顾下之前介绍过的例子：

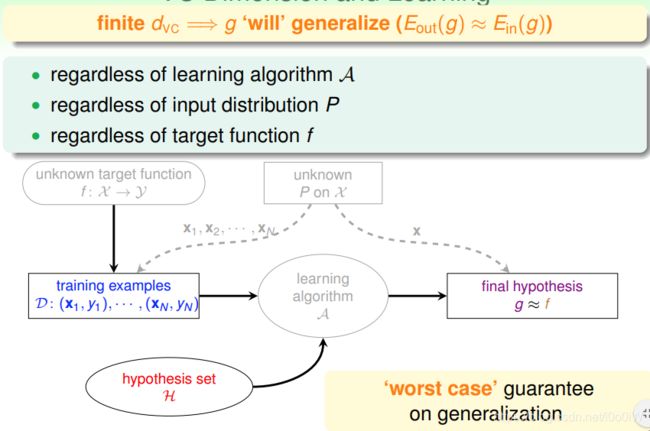
如果一个假设集合的$d_{vc}$确定了之后，那么能保证能够进行机器学习的第一个条件$E_{in}\approx E_{out}$，与算法选择、数据分布和目标函数都没有关系

（这一部分大概就是把之前讲过的东西重新定义了一下）

VC Dimension of Perceptrons

回顾之前介绍的2D PLA，这个算法的可行性其实有两条线，分别对应两个条件：

• 如果数据集是线性可分的，那么PLA是能够停止的，如果经历足够多的迭代次数，那么最终会找到理想假设$g,E_{in}(g)=0$
• 如果$N$足够大，而且2D Perceptron存在$d_{vc}=3$,根据之前介绍的理论，是能够保证$E_{out}(g)\approx E_{in}(g)$的

这是在2D情况下，如果在更高维度的情况下，$d_{vc}$是多少？

猜想：感知机输入样本维度为$d$,则$d_{vc}=d+1$

证明：

• $d_{vc}\ge d+1$

假设每一个输入都是$d$维的，我们只要能找到某种$d+1$个输入的组合可以被shatter,那么就能证明$d_{vc}\ge d+1$（这个根据$d_{vc}$的定义就能知道），所以我们就构造这样一个输入：

这个矩阵有$d+1$个输入组成，每个输入在原来基础上在第0维加上常数项1（这就是之前讲2D Perceptron的$x_0$，也就是threshold）

这个矩阵显然是可逆的，也就是说所有的$d+1$个输入都能被shatter，第一个不等式就证明了

为什么说输入矩阵可逆就等同于这些输入能被shatter？我们说两个点被shatter,就是说假设集能够将这两个点分成（1，1），（1，-1），（-1，1），（-1，-1）四种结果

分类的结果可以看作一个向量$y=(y_1,y_2,...,y_n{)}^T$,如果矩阵可逆，那么对任意一个向量$y$，总能找到$w=X^{-1}y$，也就是所有分类结果都能通过假设集得到，这就说明矩阵中的这$d+1$个输入能被shatter

• $d_{vc}\le d+1$

如果对任意$d+2$个输入，都不能被shatter,那么不等式就成立。

构造一个任意的矩阵$X$,包含$d+2$个输入，每个输入都是$d+1$维，那么这些输入向量一定是线性相关的（$n+1$个$n$维向量一定是线性相关的），也就是说某个输入向量可以用其余向量表示，然后等式两边同乘$w^T$，该输入的正负也随之确定，不存在可正可负两种可能，所以这些输入是无法被shatter的

比如下图蓝色代表正类，红色代表负类，那么$x_{d+2}$一定是正类。这里有点反证法的思想，假设能shatter，那么就有一个$w^T$,这个$w^T$刚好对应下图举例的这种分类结果。

Physical Intuition of VC Dimension

VC Dimension代表了假设空间的表达能力，即反映了H的自由度。（因为$d_{vc}$是假设集shatter的最大个数）

Interpreting VC Dimension

VC Bound:

之前的不等式说明了出现$|E_{in}-E_{out}|>ϵ$的情况的概率不超过$\delta$,那么对于$|E_{in}-E_{out}|\le ϵ$的情况重新推导不等式得到：

这个式子表现了假设集合的泛化能力：

我们更关心$E_{out}$的上界，也就是不等式组的右侧部分，根号这一项使用$\Omega$表示，代表了模型惩罚项。可以理解成模型泛化误差的一种表示，也可以看作描述模型复杂度的量

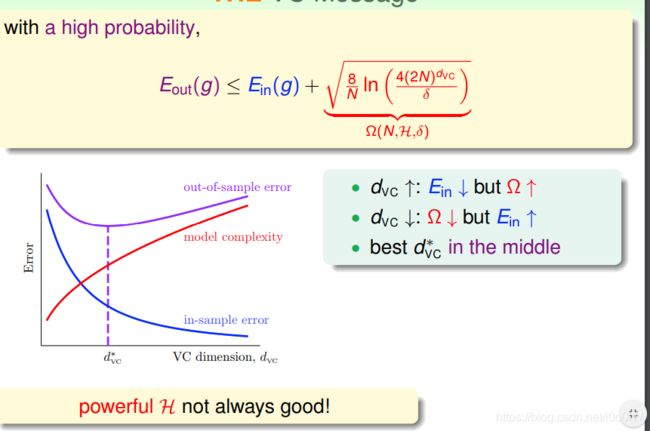
从上图可以得到结论，

$d_{vc}$增大，说明假设能shatter的点更多了，因此更有可能得到理想的分类，所以$E_{in}$会降低，但模型更加复杂了（根据$d_{vc}=d+1$，增大了$d_{v}c$也就是增加了features）,根据不等式，$E_{out}$可能会增大。

要选择合适的$d_{v}c$，才能起到比较好的泛化能力。

（模型复杂参数多导致过拟合的思想）

下面介绍样本复杂度：

如果确定了$d_{vc}$，那么样本数据选择多少才比较合适？

从这个例子当中，$N\approx 10000d_{vc}$，但是在实际中往往只需要$N\approx 10d_{vc}$就可以了，之所以如此是因为VC Bound过于宽松了，我们得到的是一个比实际大得多的上界。