reserved in total by pytorch_Pytorch的自动求导机制与使用方法(一)
转载请注明:https://zhuanlan.zhihu.com/p/148669484
本文以线性模型为例,讲解线性模型的求解的pytorch梯度实现方法.
线性模型可参考:https://zhuanlan.zhihu.com/p/148660629
要注意几个问题:
- 在PyTorch 0.4.0版本之后,Variable类已经被禁用了,所有的torch.Tensor与torch.autograd.Variable的功能可以通过torch.Tensor方法实现.
- 在pytorch里面,默认只能是标量对标量,或者标量对向量/矩阵求导!
- 要想使x支持求导,必须让x为浮点类型.
在目前的深度学习框架(PyTorch,Tensorflow,MXnet)中,自动求导功能是最核心也是最基础的功能.构建与训练深度学习的基本流程是:根据网络结构逐步搭建计算图,然后求得损失函数,之后根据计算图来计算导数,最后利用梯度下降方法更新参数.
首先根据一个例子,
import 输出结果为:
x 这里要注意:需要反向传播的数值要为浮点型,不可以为整数.
1.torch.Tensor
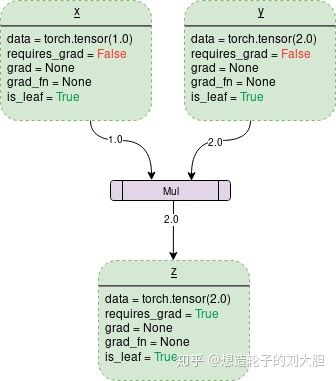
PyTorch中数据以张量(n维数组)的形式流动torch.Tensor可以用来创建张量.当Tensor的属性中requires_grad=True时,则系统会开始跟踪针对此Tensor的所有操作.其中每个操作都会有此操作想对于输入的梯度,则整个操作完成的输出张量相对于输入张量的梯度就是中间过程中所有张量的链式法则.例如,
其中
每个张量都有一个grad_fn属性用于保存张量的操作,如果这个张量为用户自己创建的,则grad_fn为None.
从图中可以看出,一个Tensor中:
- data中保存着所存有的数据
- grad中保存这梯度
- requires_grad表示是否开始追踪所有的操作历史
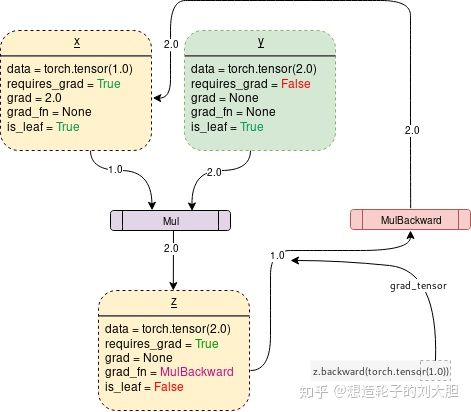
想计算导数时,调用Tensor.backward()
在调用backward()时,只有当requires_grad和is_leaf同时为真时,才会计算节点的梯度值.
2.Pytorch到底在计算什么?(雅克比矩阵和向量)
autograd类的原理其实就是一个雅克比矩阵向量积计算引擎.
设函数
则雅可比矩阵是一个m*n的矩阵:
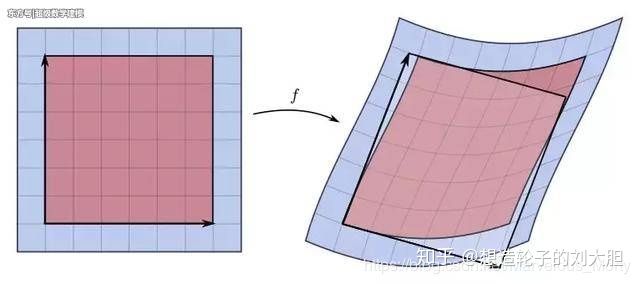
由于矩阵描述了向量空间中的运动-变换,而雅可比矩阵看作是将点
设一个pytorch张量为
根据导数的链式法则,张量
向量
当
雅克比矩阵相关内容具体可以参考https://zhuanlan.zhihu.com/p/39762178
3.例程
这一部分会详细说明一些细节性的问题,在最后会有线性模型的例程.
在上边说过叶子节点(is_leaf),如果有多个叶子节点,这些节点的is_leaf都是False,则整体才是不可求导的,例程如下:
import 上边例程中,关闭了y的梯度追踪,但是x的梯度追踪还开着,所以z是可以求导(print(z.requires_grad)为True).
当x也关闭了梯度追踪,那么z也无法求导(print(z.requires_grad)为False).
当计算梯度之后,y是不可求导的,这时候y.grad为None.
可以通过x.requires_grad_(True/False)修改叶子节点的可导与不可导.
Tensor.backward()方法
.backward()默认计算对计算图叶子节点的导数,中间过程的导数是不计算的.例程如下:
x 结果如下:
tensor上边的例子大多都是标量对标量的求导例程.
标量对向量求导:
下面来说明一个线性模型的雏形版本,输入为向量,输出为标量.设一个输入为
偏导数为:
例程:
x 标量对矩阵求导:
设输入为一个矩阵(2*3)
第一次操作:
第二次操作,Y上每个元素平方:
第三次操作,Z上所有元素平均值:
偏导数为:
import 向量/矩阵对向量/矩阵求导
backward()默认输出为标量,这是因为我们在深度学习中最后的loss为一个标量,这是常用的方式.
当输出为向量或矩阵时,需要通过地一个参数gradient来实现.gradient参数的维度与最终的输出要保持一致,gradient中每个元素表示为对应的最终输出中相同位置元素所对应的权重.
例程:
import 输出为:
tensor([[ 3., 5., 7.],
[ 9., 11., 13.]])
tensor([[ 3.0000, 0.5000, 0.0700],
[ 9.0000, 11.0000, 13.0000]])线性模型的求解过程
import 在这段代码中要注意,如果将
weight更换为
weight = weight - learning_rate/mini_batch*weight.grad.data会报错,因为weight表示了一个新的对象,他的名字还是weight,变为了中间节点,默认情况下是无法获取其梯度的,可以采用weight.retain_grad()来处理.
参考:
1.http://pytorch123.com/SecondSection/autograd_automatic_differentiation/
2.PyTorch的自动求导机制详细解析,PyTorch的核心魔法_AI公园-CSDN博客
3.https://blog.csdn.net/qq_27825451/article/details/89393332