分别使用BP神经网络和SVM支持向量机进行乳腺癌识别matlab仿真,输出识别率,召回率以及F1

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       乳腺癌是全球第二常见的女性癌症。2012年，它占所有新癌症病例的12%，占所有女性癌症病例的25%。当乳腺细胞生长失控时，乳腺癌就开始了。这些细胞通常形成一个肿瘤，通常可以在x光片上直接看到或感觉到有一个肿块。如果癌细胞能生长到周围组织或扩散到身体的其他地方，那么这个肿瘤就是恶性的。

       构建一个算法，通过查看活检图像自动识别患者是否患有乳腺癌。算法必须非常精确，因为人的生命安全是第一的。

BP:

       人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果。作为一种智能信息处理系统，人工神经网络实现其功能的核心是算法。BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。
        基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

       BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定，并且随着结构的差异其性能也有所不同。但是BP神经网络也存在以下的一些主要缺陷。

①学习速度慢，即使是一个简单的问题，一般也需要几百次甚至上千次的学习才能收敛。

②容易陷入局部极小值。

③网络层数、神经元个数的选择没有相应的理论指导。

④网络推广能力有限。

SVM:

        SVM是由模式识别中广义肖像算法（generalized portrait algorithm）发展而来的分类器  ，其早期工作来自前苏联学者Vladimir N. Vapnik和Alexander Y. Lerner在1963年发表的研究  。1964年，Vapnik和Alexey Y. Chervonenkis对广义肖像算法进行了进一步讨论并建立了硬边距的线性SVM。此后在二十世纪70-80年代，随着模式识别中最大边距决策边界的理论研究 、基于松弛变量（slack variable）的规划问题求解技术的出现，和VC维（Vapnik-Chervonenkis dimension, VC dimension）的提出，SVM被逐步理论化并成为统计学习理论的一部分 。1992年，Bernhard E. Boser、Isabelle M. Guyon和Vapnik通过核方法得到了非线性SVM 。1995年，Corinna Cortes和Vapnik提出了软边距的非线性SVM并将其应用于手写字符识别问题，这份研究在发表后得到了关注和引用，为SVM在各领域的应用提供了参考。

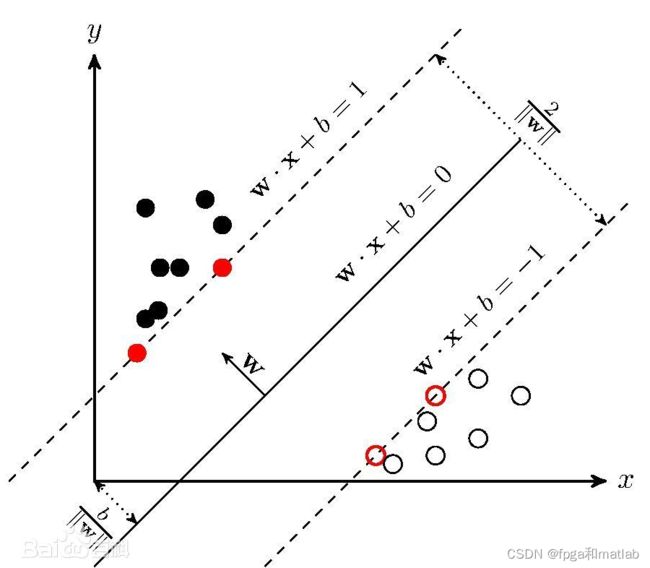
       支持向量机本质上是从在线性分类算法的基础上发展而来的，就如Logistic 逻辑回归算法一样，只需给线性函数“套”上一层 Logistic “马甲”，就可以用线性模型来解决离散数据的分类问题。对于支持向量机来说，要解决分类问题，其过程则更为复杂。下

二、核心程序

BP:

I1  = find(T==1);
I2  = find(T==2);
idx1= [I1(1:floor(L*length(I1)));I2(1:floor(L*length(I2)))];
idx2= [I1(1+floor(L*length(I1)):end);I2(1+floor(L*length(I2)):end)];

for j = 1:MTKL
j
rng(j);
Ptrain = P(idx1,:);
Ptest  = P(idx2,:);

Ttrain = T(idx1);
Ttest  = T(idx2);


%数据输入
net2 = newff(Ptrain',Ttrain',4,{'tansig', 'purelin'}, 'traingd'); % 隐含层有5个神经元
net2.trainParam.goal   = 1e-5;
net2.trainParam.epochs = 1000;
net2.trainParam.lr     = 0.0025;
net2.trainParam.showWindow = 0;
net2 = train(net2,Ptrain',Ttrain');
y    = [round(sim(net2,Ptest'))]';

[A,~]= confusionmat(Ttest,y);
%计算-1类的评价值
c1_precise(j) = A(1,1)/(A(1,1) + A(2,1));
c1_recall(j)  = A(1,1)/(A(1,1) + A(1,2));
c1_F1(j)      = 2 * c1_precise(j) * c1_recall(j)/(c1_precise(j) + c1_recall(j));
%计算1类的评价值
c2_precise(j) = A(2,2)/(A(1,2) + A(2,2));
c2_recall(j)  = A(2,2)/(A(2,1) + A(2,2));
c2_F1(j)      = 2 * c2_precise(j) * c2_recall(j)/(c2_precise(j) + c2_recall(j));

end
UP30

SVM:

C     = 0.1;
gamma = 0.005;
cmd = ['-s 1',' -t 3',[' -c ', num2str(C)],[' -g ',num2str(gamma)],' -p 0.01']; 
%训练比例
L   = 0.5;
P   = breast(:,1:9);
T   = round(breast(:,end)/2);

MTKL= 100;
I1  = find(T==1);
I2  = find(T==2);
idx1= [I1(1:floor(L*length(I1)));I2(1:floor(L*length(I2)))];
idx2= [I1(1+floor(L*length(I1)):end);I2(1+floor(L*length(I2)):end)];
 
for j = 1:MTKL
j
rng(j);
 
Ptrain = P(idx1,:);
Ptest  = P(idx2,:);

Ttrain = T(idx1);
Ttest  = T(idx2);


%数据输入
svm_models = svmtrain(Ttrain,Ptrain,cmd);
[y,error1] = svmpredict(Ttest,Ptest,svm_models);


[A,~]= confusionmat(Ttest,y);
%计算-1类的评价值
c1_precise(j) = A(1,1)/(A(1,1) + A(2,1));
c1_recall(j)  = A(1,1)/(A(1,1) + A(1,2));
c1_F1(j)      = 2 * c1_precise(j) * c1_recall(j)/(c1_precise(j) + c1_recall(j));
%计算1类的评价值
c2_precise(j) = A(2,2)/(A(1,2) + A(2,2));
c2_recall(j)  = A(2,2)/(A(2,1) + A(2,2));
c2_F1(j)      = 2 * c2_precise(j) * c2_recall(j)/(c2_precise(j) + c2_recall(j));
clc
end
idx=[];
for i =1:MTKL
    if isnan(c1_precise(i))==1 | isnan(c1_recall(i))==1 |  isnan(c1_F1(i))==1 | isnan(c2_precise(i))==1 | isnan(c2_recall(i))==1 |  isnan(c2_F1(i))==1
       idx=[idx,i];  
    end
end
up31

三、测试结果

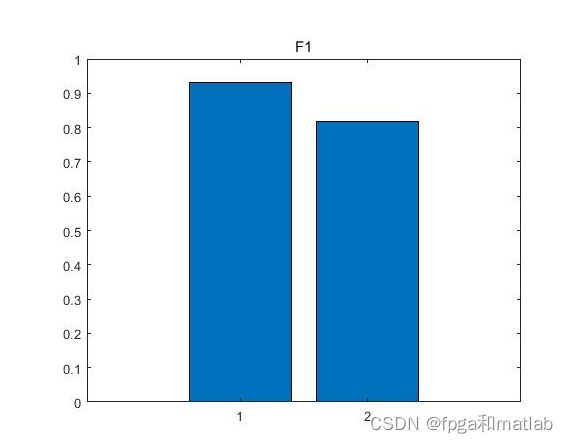
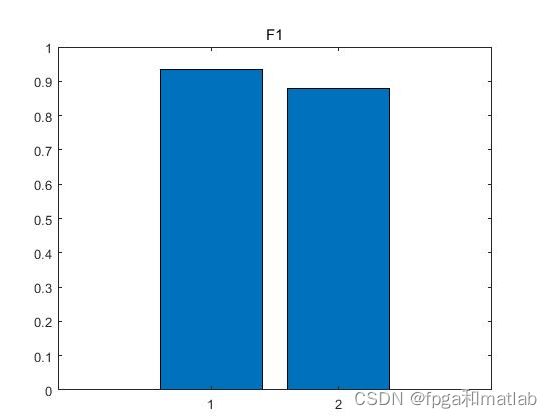
matlab2021a测试结果如下

BP:

 

 SVM: