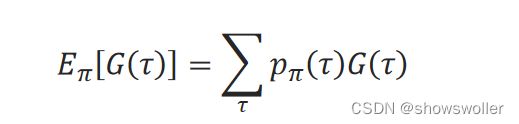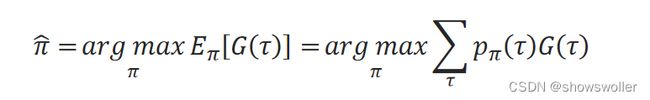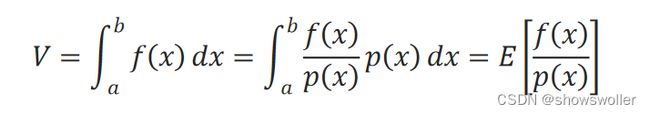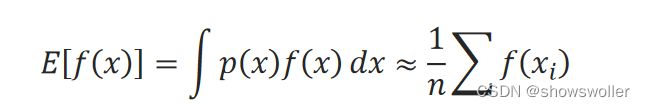【Python强化学习】马尔可夫决策过程与蒙特卡洛近似算法讲解（图文解释）

觉得有帮助请点赞关注收藏~~~

马尔可夫决策过程

如果系统的下一个状态s_t+1的概率分布只依赖于它的前一个状态s_t，而与更早的状态无关，则称该系统满足马尔可夫性。即对任意的时间t，对任意的状态s_t、s_t+1，均有下面的条件概率等式：

P(s_t+1│s_t)=P(s_t+1│s_1,s_2,…,s_t)

马尔可夫性完全忽视了过往历史的影响，大大减少了系统建模的复杂度和计算量，是常用的建模简化假定。

随机性策略

用A和S分别表示主体的动作变量和环境的状态变量。用概率来描述主体的随机性策略：

π(a│s)=P(A_t=a│S_t=s)

其中，A_t和S_t分别表示t时刻的主体动作和环境状态。 设共有N种状态，共有M个动作，如果能确定任一具体状态s_i(1≤i≤N)条件下任一具体动作a_j(1≤j≤M)的概率，那么该随机性策略就完全确定了。 用概率来描述环境模型，可表示为条件概率：

P_ss^′^a=P(S_t+1=s^′│S_t=s,A_t=a)

如果能得到从任一状态和任一动作组成的联合条件下任一状态的概率，那么环境模型P_ss^′^a也就确定了。该条件概率也称为环境的状态转移概率。

在指定状态s和动作a时，下一步要进入的状态并不唯一，因此，得到的回报r也不唯一，可用数学期望来描述在指定状态s和动作a时的回报的数学期望为：

R_s^a=E[r^′]=∑_s^′∈S▒P_ss^′^ar^′

r^′表示进入到下一个状态s^′得到的立即回报。

如果主体策略、环境模型和回报都确定了，那么，主体可以基于当前或长远两种考虑来选择下一步的动作A：

1）基于当前的考虑，就是依据现状S，选择一个动作A，使得环境进入到一个可得到尽量多立即回报r^′的状态S^′。

2）基于长远的考虑，就是还要考虑下一步的回报，也就是说要使下一步的状态进入到一个便于在未来得到尽量多累计回报的状态。

强化学习的目标是着眼长远，而非当前。

未来累计折扣回报

称主体的一次尝试过程为轨迹（episode），用τ=(s_0,a_0,s_1,a_1,s_2,a_2,…)表示，它是对状态和动作的按时间顺序的记录。

对一个轨迹，得到所有时刻进入新状态的立即回报，记为立即回报序列：R=(r_1,r_2,r_3,…)。

用所谓的未来累积折扣回报（Cumulative Future Discounted Reward）来刻画长远考虑。在某轨迹中，从时刻t开始的未来累积折扣回报定义为：

G_t=r_t+1+γr_t+2+γ^2r_t+3+…+γ^nr_t+n+1+…, γ∈[0,1] γ∈[0,1]称为折扣系数，通过不同的折扣系数可以调节未来的立即回报对当前的影响。

G_t可以写成递推形式： G_t=r_t+1+γr_t+2+γ^2r_t+3+…+γ^nr_t+n+1+…=r_t+1+γ[r_t+2+γ^1r_t+3+…+γ^n−1r_t+n+1+…]=r_t+1+γG_t+1

马尔可夫决策过程可用五元组〈S,A,P,R,γ〉来表示，在这里，S表示可能状态的集合，A表示可能动作的集合，P表示状态转移概率，R是回报函数，γ是折扣系数。

在主体的随机尝试中，某一轨迹τ出现的概率记为p_π(τ)。 对轨迹τ=(s_0,a_0,s_1,a_1,s_2,a_2,…)： p_π(τ)=π(a_0│s_0)P_s_0s_1^a_0π(a_1│s_1)P_s_1s_2^a_1π(a_2│s_2)P_s_2s_3^a_2…

显然，在环境模型P_ss^′^a已经确定的条件下，该概率由策略π确定，也就是说在不同的策略下，同一条轨迹出现的概率可能会有差异。

记轨迹τ的未来累积折扣回报为G(τ)。G(τ)的数学期望为：

式中，τ表示任何可能的轨迹。 在马尔可夫决策过程框架中，强化学习的目标就是找到使未来累积折扣回报的期望最大的策略π ̂：

 

直接求解策略和基于值函数求解策略

想办法从所有候选策略中寻找最优策略的思路称为直接求解策略的求解方法。

间接求解策略的方法是先计算所谓的值函数，然后通过值函数来求得最优策略。该类方法称为基于值函数的求解方法。 状态值函数V_π(s)是在指定策略π时，限定起始状态为s时的未来累积折扣回报的数学期望：

V_π(s)=E_π[G_t|S_t=s┤]=E_π[r_t+1+γr_t+2+γ^2r_t+3+…|S_t=s┤]

动作值函数Q_π(s,a)是在指定策略π时，除了限定起始状态为s，还进一步限定执行动作为a时的未来累积折扣回报的数学期望：

动作值函数体现了在指定状态下，执行指定动作的“价值”。如果能够得到每个动作值函数的值，那么，最优策略就是在当前状态下，选择使该值最大的动作。

蒙特卡洛近似

随机近似方法的基本思想是通过大量的随机样本去探索系统，得到有关系统的近似模型。

用随机近似法来对函数f(x)的积分 V=∫_a^b▒f(x)□dx的进行估计，还可以采用下面的思路。 设p(x)是x在(a,b)上的概率密度函数，则有：

 

也就是说，可以用f(x)/p(x)的数学期望来估计积分V。 如果x是均匀分布的，那么p(x)=1/b−a。在(a,b)内均匀采样，得到x_1,x_2,…,x_n，根据大数定律，可以由平均值来估计期望：

 

如果求函数f(x)关于 x的分布p(x)的期望E[f(x)]=∫▒p(x)f(x)□dx，可以先依概率p(x)采样x_i，然后根据大数定律用样本均值来近似：

 

这种基于随机采样来求解问题的方法也称为蒙特卡罗（Monte Carlo）法，也称为统计实验方法，或者统计模拟方法

蒙特卡罗法的随机采样思想与强化学习的尝试学习思想是相近的，因此它在强化学习中占有重要地位。在强化学习中，通过蒙特卡罗法可以对未知环境模型进行近似的建模，帮助求得最优策略。

 创作不易 觉得有帮助请点赞关注收藏~~~