【深度学习】DETR解读

DETR解读

1 贡献点

• DETR takes object detection as a direct set prediction problem, which is actually a NMS-free method, leveraging the one-to-one label assignment.
• DETR utilizes the emerging transformer for decoding image representations to a fixed-size set of predictions.
• DETR uses a set-based global loss that forces unique predictions.

其实早在2016年，论文（End-to-End People Detection in Crowded Scenes, CVPR 2016）就提出了类似的框架，DETR的不同之处主要在于：

• 在解码阶段使用vision transformer模型而非LSTM；
• 利用vision transformer的特性，同时输出大小为$N$的预测集合，而不像传统RNN逐步输出单个预测。

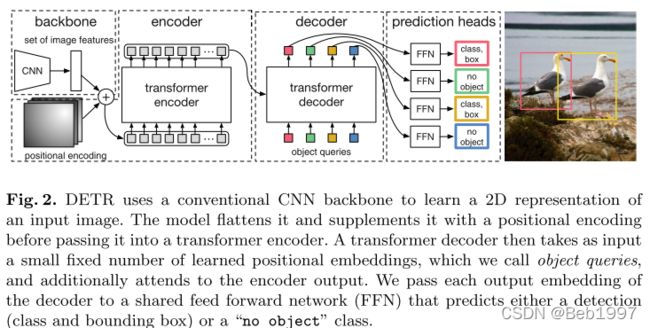
2 模型结构

DETR模型的前向计算流程如下：

• 使用骨干网络获取图像特征，可以是CNN模型 (e.g. ResNet)，也可以是Vision Transformer模型 (e.g. SwinT)；
• 使用transformer encoder (self-attention only)和transformer decoder (both self-attention & cross-attention)进一步增强特征；
• 使用MLP(or FFN)输出$N$个预测框的位置和大小，使用带softmax的线性层（即逻辑回归）为每个框的目标分类。

2.1 Backbone

假设$x_i\in {\mathbb{R}}^{3\times H_i\times W_i}$表示某张RGB图像，由于每张图像的尺寸有差异，故而将所有图片转换为$x_i\in {\mathbb{R}}^{3\times H_0\times W_0}$以组成小批量。其中$H_0=max\{H_i\}$，$W_0=max\{W_i\}$，通过在图像的右边和底边填充0实现。开源代码中的NestedTensor就是为了这个目的。

class NestedTensor(object):
    def __init__(self, tensor, mask):
        self.tensor = tensor  # img tensor itself
        self.mask = mask  # binary mask containing 1 on padded pixels and 0 on others

    def to(self, device):
        cast_tensor = self.tensor.to(device)
        cast_mask = self.mask.to(device) if self.mask is not None else None
        return NestedTensor(cast_tensor, cast_mask)

    def decompose(self):
        return self.tensor, self.mask

    def __repr__(self):
        return str(self.tensor)

为了表示方便，省略批量维度，设输入图像$x_{img}\in {\mathbb{R}}^{3\times H_0\times W_0}$，通过骨干网络后得到特征图$f\in {\mathbb{R}}^{C\times H\times W}$，以ResNet101为例，$C=2048$，$H=\frac{H_0}{32}$，$W=\frac{W_0}{32}$。图像对应的$mask$直接通过双线性插值匹配$f$的大小。为了降低transformer部分的运算量，使用线性映射(如$1\times 1conv$)将特征图$f$降维，得到$z_0\in {\mathbb{R}}^{d\times H\times W}$作为后续输入，在DETR中，$C:2048\to d:256$.

2.2 Transformer

2.2.1 Position Embedding

Vision transformer中position embedding(PE)需要同时考虑图像的$height$和$width$两个维度，当前主要采用两种方式：

• 可学习PE，如ViT (An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale, ICLR 2021)；
• 同原始transformer一致，使用固定不变的三角函数PE，如DETR。

对于特征图$z_0\in {\mathbb{R}}^{d\times H\times W}$，相应的位置编码$PE\in {\mathbb{R}}^{d\times H\times W}$。对于位置$(h,w)$，前$d/2$维表示$height$方向的位置编码，后$d/2$维表示$width$方向的位置编码，当然反之亦可，DETR中$d/2=128$。令$i$表示位置编码的维度，则：

$P{E}_{h,2i}=sin(\frac{h}{10000^{2i/128}})$，$P{E}_{h,2i+1}=cos(\frac{h}{10000^{2i/128}})$，$i=0,1,2,...,63$

$P{E}_{w,2i}=sin(\frac{w}{10000^{2i/128}})$，$P{E}_{w,2i+1}=cos(\frac{w}{10000^{2i/128}})$，$i=0,1,2,...,63$

为什么底数取$10000$呢，玄学！

import math
import torch
import torch.nn as nn


class LearnablePE(nn.Module):
    def __init__(self, pe_dim):
        super(LearnablePE, self).__init__()
        self.row_embed = nn.Embedding(50, pe_dim)  # 50 is larger than img height
        self.col_embed = nn.Embedding(50, pe_dim)
        self._reset_params()

    def _reset_params(self):
        """
        nn.Embedding.weight is by default initialized from N(0, 1),
        here we use initialization from U(0, 1)
        """
        nn.init.uniform_(self.row_embed.weight)
        nn.init.uniform_(self.col_embed.weight)

    def forward(self, x: NestedTensor):
        x = x.tensor
        h, w = x.shape[-2:]
        i = torch.arange(w, device=x.device)
        j = torch.arange(h, device=x.device)
        x_emb = self.col_embed(i)  # look up for learnable embeddings by index
        y_emb = self.row_embed(j)
        pos = torch.cat([x_emb.unsqueeze(0).repeat(h, 1, 1),
                         y_emb.unsqueeze(1).repeat(1, w, 1)],
                        dim=-1).permute(2, 0, 1).unsqueeze(0).repeat(x.size(0), 1, 1, 1)
        return pos


class FixedPE(nn.Module):
    def __init__(self, pe_dim, temperature=10000, normalize=True, scale=None):
        super(FixedPE, self).__init__()
        self.pe_dim = pe_dim
        self.t = temperature
        if scale is not None and normalize is False:
            raise ValueError("normalize should be True if scale is passed")
        self.norm = normalize
        self.scale = scale if scale is not None else 2 * math.pi

    def forward(self, x: NestedTensor):
        assert x.mask is not None
        not_msk = ~x.mask
        x = x.tensor
        y_embed = not_msk.cumsum(1, dtype=torch.float32)
        x_embed = not_msk.cumsum(2, dtype=torch.float32)
        if self.norm:  # normalize to [0, 2*PI]
            y_embed = y_embed / (y_embed[:, -1:, :] + 1e-6) * self.scale
            x_embed = x_embed / (x_embed[:, :, -1:] + 1e-6) * self.scale

        dim = torch.arange(self.pe_dim, dtype=torch.float32, device=x.device)
        dim = self.t ** (2 * (dim // 2) / self.pe_dim)

        pos_x = x_embed[:, :, :, None] / dim
        pos_y = y_embed[:, :, :, None] / dim

        pos_x = torch.stack([pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()], dim=4).flatten(3)
        pos_y = torch.stack([pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()], dim=4).flatten(3)

        pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
        return pos

由于骨干网络的输出即transformer部分的输入，所以在DETR官方开源代码中，将PE的获取放在了backbone部分，并定义Joiner类，得到骨干网络不同stage的输出，和相对应的PE。

2.2.2 Encoder & Decoder

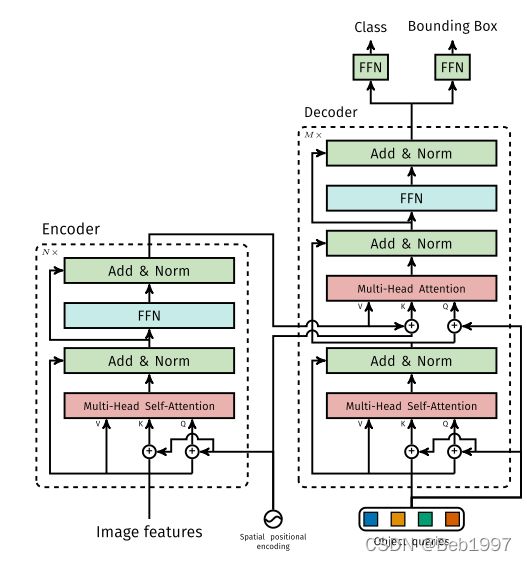
DETR所使用的transformer结构有如下特点：

• 原始transformer仅在输入使用位置编码(position embedding, PE)，DETR在每一个注意力层之前均使用；
• DETR中，PE仅在$Q$和$K$上使用。
  

骨干网络的输出$z_0\in {\mathbb{R}}^{d\times H\times W}$和对应的位置编码$PE\in {\mathbb{R}}^{d\times H\times W}$均被reshape到${\mathbb{R}}^{(HW)\times d}$作为encoder部分的输入，记encoder的输出为$memory\in {\mathbb{R}}^{(HW)\times d}$。

decoder的输入包含：(1) encoder的输出$memory\in {\mathbb{R}}^{(HW)\times d}$，(2) 可学习的object query，记为$query\in {\mathbb{R}}^{N\times d}$，(3) $target\in {\mathbb{R}}^{N\times d}$和$query$形状相同，初始化为0。decoder的输出为$out\in {\mathbb{R}}^{N\times d}$，DETR中取$N=100,d=256$.

• 在self-attention部分，$Q$，$K$和$V$均由$target$得到，$Q$和$K$使用位置编码，即$Q,K=target+query$，$V$无位置编码，即$V=target$；
• 在cross-attention部分，$Q$由self-attention的输出结合位置编码$query$得到，$K$由encoder部分的输出结合位置编码$PE$得到，即$K=memory+PE$，$V$不使用位置编码，即$V=memory$。

2.3 Head

假设$y_i=(c_i,b_i)$为第$i$个GT标注，其中$c_i\in \{\varnothing ,0,1,2,...\}$为目标的类别标注，$b_i=(b_{i,x},b_{i,y},b_{i,h},b_{i,w})$分别表示检测框的中心坐标$(b_{i,x},b_{i,y})$、相对高度和宽度。本节标题Head即为原文中Prediction Feed-Forward Networks (FFNs)，包含两部分：

• 用于为目标分类的逻辑回归层(线性映射+softmax)，定义为class_head=nn.Linear(d, num_classes+1)，"+1"是因为引入了$\varnothing$类别标注；
• 用于检测框回归的MLP，定义为box_head=MLP(input_dim=d, hidden_dim=d, output_dim=4, num_layers=3)。

3 损失函数

假设$y=\{y_i|y_i=(c_i,b_i){\}}_{i=1}^N$表示$N$个GT标注，$\hat{y}=\{{\hat{y}}_i|{\hat{y}}_i=({\hat{c}}_i,{\hat{b}}_i){\}}_{i=1}^N$表示模型的$N$个预测。由于DETR采用了one-to-one label assignment的方式，故而需要将每一个预测的box和标注box匹配起来，文章采用匈牙利算法(Hungarian algorithm)来实现，即找到代价最小的一种匹配(match)方式。

• 论文中，${\mathcal{L}}_{match}$表示代价函数，包含分类${\mathcal{L}}_{cls}$和预测框${\mathcal{L}}_{box}$两个部分；
• ${\mathcal{L}}_{box}$又包含了IoU损失${\mathcal{L}}_{iou}$和${\ell }_1$损失两部分；

损失函数每部分的具体细节可参考论文，比较直观和简单。匈牙利算法可以使用scipy库中的linear_sum_assignment实现。

4 相关工作

基于DETR，已有后续相关工作，如：

• Deformable DETR (Deformable DETR: Deformable Transformers for End-to-End Object Detection, ICLR 2021)结合可变形卷积的思想，在计算注意力时将$K$稀疏采样，降低了计算的复杂度，在维持模型整体计算量相近的同时引入FPN特征，较好地解决了DETR小目标检测性能差的问题；
• Sparse DETR (Sparse DETR: Efficient End-to-End Object Detection with Learnable Sparsity)进一步将$Q$稀疏化，降低了模型整体的计算复杂度；
• MaskFormer (Per-Pixel Classification is Not All You Need for Semantic Segmentation, NeurIPS 2021)基于DETR统一了语义分割、实例分割和全景分割，并取得了不错的效果。