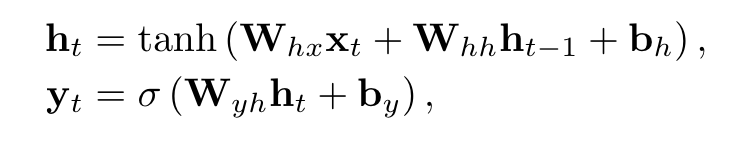深度知识追踪(DKT)详解与Python实现

之前总结过了知识追踪的发展历程，2015年Chris Piech等人第一次将深度学习应用于知识追踪，效果显著，自此出现了大量改进的DKT模型。深度知识追踪模型可以实现对学生的知识状态的动态追踪，相比于之前只能针对测评数据静态诊断的模型，更适用于当前的测评场景。

本文对这篇经典论文进行讲解：Deep Knowledge Tracing

一、概述

知识追踪的任务是对学生的知识进行建模，这样我们就可以准确地预测学生在未来的互动中将如何表现。简单来说，就是我们有了学生的历史做题序列数据，我们可以通过学生与题目的交互结果得出学生当前的知识状态以及题目的信息，这样就可以对学生在题目上的表现进行预测。以往的模型大多依赖于人工定义的交互函数，比如IRT模型，定义了学生能力参数和题目的难度、区分度、猜测性参数，也有改进的不依赖交互函数的，比如刘淇提出的NeuralCD模型，但是仍更适用于“对学生历史做题数据测评”，没有办法动态追踪，存在冷启动问题。

深度知识追踪，将时间上“深度”的灵活递归神经网络(RNN)应用到知识追踪任务中。这一系列模型使用大量人工“神经元”来表示潜在的知识状态及其时间动态，并允许从数据中学习学生知识的潜在变量表示，而不是硬编码。解决了冷启动问题，并且可以动态追踪学生的知识状态变化。

这篇论文的主要贡献：

1. 提出一种将学生交互编码作为递归神经网络输入的新方法；
2. 相较于以往的知识追踪模型，AUC比之前最好的结果提高了25%；
3. 这篇论文提出的模型不需要专家标注；
4. 可以发现练习题的影响并且生成改进的练习课程。

从整体描述一下知识追踪的任务：我们有了一个学生的历史答题序列  ，然后我们要预测这个学生在  题上的表现。一般，学生的答题记录采用  的形式，其中  表示题目标签(最简单可以理解为题目id)，  表示作答结果(目前大多是0/1计分，是否答对)，当预测的时候，就是将题目标签  输入到模型中，模型输出预测结果  。

可以看下图的例子(一个学生学习8年级数学的知识追踪可视化)，先来大概理解下深度知识追踪是做什么的：

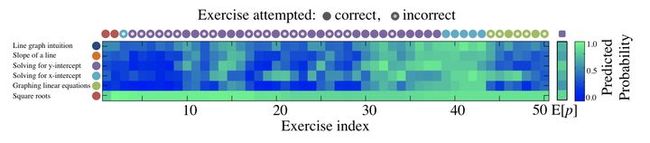
图 1

这个学生一共做了50道题(横轴)，在深度知识追踪中，每道题关联一个知识点，在上面这50道题中，共考察了6个知识点，如左边显示，深蓝色表示“Line graph intuition”这个知识点，橘黄色表示“Slope of a line”这个知识点等等，学生的实际答题情况由图上方的圆圈表示，圆圈的颜色表示了这道题考察的是哪个知识点，实心圆圈表示答对，空心圆圈表示答错。图中间的蓝绿色网格表示模型的预测结果，由深蓝色到浅绿色表示答对概率越来越高。具体解释一下，这个学生开始答对了两道红棕色的题(考察知识点“Square roots”)，那么网格前两列，对于知识点“Square roots”模型预测其作答准确率就很绿(答对概率高)，而对于其它没考察的知识点就很蓝(答对概率低)，第三道题做错一道浅蓝色的题，第四到第九道题都是做错了紫色的题，那么对浅蓝色知识点和紫色知识点会预测其答对概率降低。

二、相关工作

这里就不做过多介绍了，基础就是要弄清楚以往的知识追踪模型存在的限制，然后要了解学习递归神经网络的概念。

三、深度知识追踪

我们人类的学习过程受到许多因素，比如学习资料、上下文、做题的顺序、还有个人的学习能力等，但是许多的属性很难量化。这篇论文应用了两种递归神经网络，一个是普通的基于Sigmoid的RNN，另一个是长短期记忆模型(LSTM)。

3.1 模型

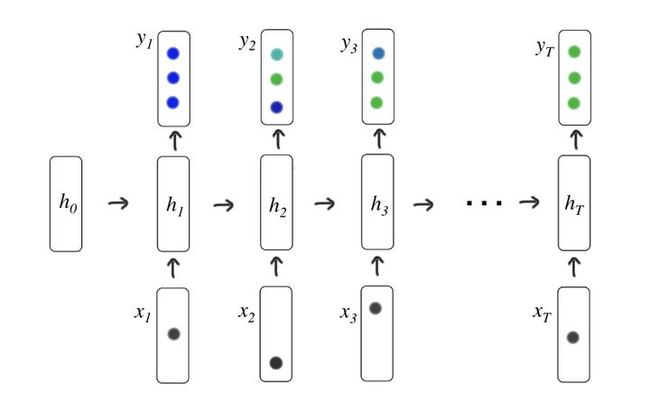
传统的递归神经网络(RNNs)将输入序列  映射为输出序列  ，这是通过计算一系列隐藏状态  实现的，隐藏状态可以被看做来自过去观测的相关信息的编码，用于对未来的预测，如下图所示：

其中每次网络的结构是相同的，因此叫递归神经网络，输入  是学生动作的独热编码或压缩表示，输出  是预测学生答对练习题的概率的向量，由下面公式定义：

其中  和Sigmoid函数  都是按元素应用的，输入权重矩阵  、递归权重矩阵 、隐藏层偏置  、输出权重矩阵  、输出层偏置  是模型待训练参数，还需要定义初始状态  。

长短期记忆(LSTM)网络是RNN的一种更复杂的变体，通常被证明更强大。在LSTM中，隐藏层保留它们的值，直到通过“遗忘门”的动作将其显式清除。因此，它们更自然地在许多时间步长内保持信息，这被认为使它们更容易训练。此外，隐藏单元使用乘法交互进行更新，因此它们可以对相同数量的潜在单元执行更复杂的转换。LSTM的更新公式比RNN复杂得多：

3.2 输入输出时间序列

为了对RNN或LSTM进行关于学生与题目交互的训练，需要将这些交互转换为固定长度的输入向量序列  ，根据这些交互的性质，我们使用两种方法来实现（整个模型只关注题目所属的知识点，以及做题结果）：

（1）one-hot编码

假设我们模型中的数据共考察了M个知识点，所有题目都属于这M个知识点，我们将输入  设置为学生交互元组  的一次one-hot编码，  表示题目标签，  表示是否答对(0/1)，对于某一道考察了第i个知识点的题，做对时向量的第M+i个位置为1，其余位置为0；做错时第i个位置为1，其余位置为0，向量总长度为2M，因此  ，为什么将题目标签和是否答对连接起来呢？因为发现单独表示会降低性能。one-hot 的表示比较方便，但是一旦知识点的数量非常大之后，向量就会变得高维、稀疏。

举个例子：

比如一个学生做了8道题，这8道题考察了5个知识点(假设每道题考察1个知识点)：

题目id	知识点id	作答结果
1	2	0
2	4	1
3	1	1
4	1	1
5	2	0
6	5	0
7	5	1
8	3	0

那么这个学生的做题序列输入编码：

（2）通过压缩感知机算法降维

在这篇论文中没有用到压缩感知机算法降维，但是当数据集考察的知识点数目特别多时，上面的one-hot编码就会非常大，向量就会变得高维、稀疏，因此需要一些手段进行降维。这篇论文就提出了压缩感知机这个算法，它其实是一个针对信号采样的技术，在采样过程中完成了数据的压缩。通过压缩感知算法将高维稀疏的输入数据进行压缩到低维空间(  )中。

压缩感知机算法暂时还没深入看，以后看了再补充

3.3 最优化

我们训练模型是预测学生对题目答对的概率(得分)，因此可以基于预测得分和实际得分(答对1/答错0)构成的损失函数进行反向传播。当学生做到第  道题，令  是上面讲过的one-hot编码，  是二进制交叉熵，那么对学生做这道题预测得到的损失是  ，对单个学生整个做题序列的损失是：

该目标是最小化的随机梯度下降的小批量。

为了防止训练过程中的过拟合，在计算  时，我们会对  进行Dropout，也就是将隐藏层单元中的部分进行丢弃。

可以参考： 深度学习中Dropout原理解析_Microstrong-CSDN博客_dropout

为了防止反向传播过程中的梯度爆炸，我们通过截断范数高于阈值的梯度长度来进行(确定一个范围，如果参数的梯度超过了，直接裁剪让其等于范围上界)。

可以参考： 做大饼馅儿的韭菜：深度学习之3——梯度爆炸与梯度消失
小崔：深度学习之梯度裁剪（Gradient Clipping）

四、教育场景应用

知识追踪的训练目标是根据学生过去的活动来预测他们未来的表现。这是直接有用的。例如，如果学生的能力经过持续的评估，就不再需要正式测试。DKT模型可以推动一些其它改进。

4.1 改善课程设置

DKT模型最大的潜在影响之一是选择最佳的学习题目顺序呈现给学生。给定一个训练好的隐藏知识状态的学生，我们可以查询我们的RNN模型来计算，如果我们布置给他一个练习题，预期的知识状态是什么。比如图1的这个例子，在学生做了50道题之后，我们可以测试并展示每一个不同的第51道题，计算他在给定题目下的预期知识状态。对于这个学生，预计最优的下一个问题是考察“Solving for x-intercept”这个知识点的题（简单理解，就是这个知识点这个学生掌握情况最差，应该多加练习）。

4.2 发现习题间的关系

DKT模型还可以应用于发现数据中的潜在结构或概念的任务，该任务通常由人类专家执行。我们通过给每个有向的练习i和j对分配一个影响  来解决这个问题：

其中  表示，学生在作答了题目i后，再作答题目j的答对概率。

五、数据集

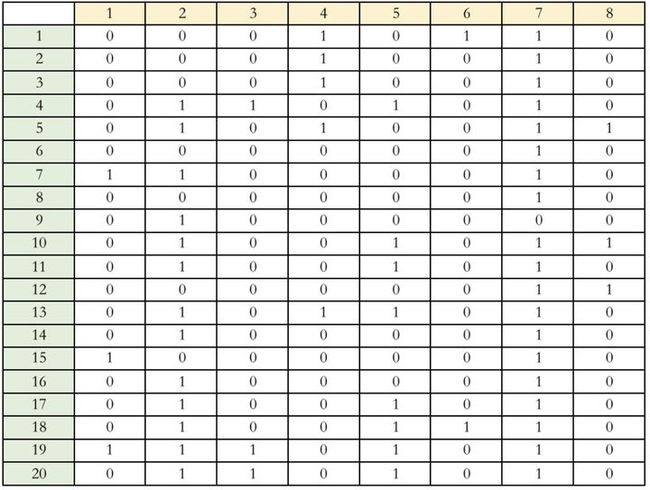
原论文中共使用了三个数据集，但我为了更快测试没有用这三个数据集，用了一个只有536条的小样本集，是FrcSub数据集，这个数据集总共有20道题，共考察了8个知识点，如下图所示，是这20道题的Q矩阵，显示了每道题考察了哪个知识点。

可以看出，每道题不止考察1个知识点，考察了多个知识点，这时我们可以把one-hot换成muti-hot，比如第一道题如果答错了，输入编码就是：

（需要数据集，可以评论留言）

六、代码

这里参考的刘淇大佬实验室的代码，简单改了一下：

BigData Lab @USTC 中科大大数据实验室​github.com/orgs/bigdata-ustc/repositories

PS：下面就写下训练过程

import torch
import torch.nn as nn
import time
import random
import torch.nn.functional as F
import pandas as pd
from collections import namedtuple, defaultdict

# 数据格式
"""
 {学生id: [
        Item(exer_id=.., score=.., knowledge_code=[..]),
        Item(exer_id=.., score=.., knowledge_code=[..]),
        ...
]}
"""

# 学生做题序列，其中bias用于执行考试内打乱
Item = namedtuple('Item', ['exer_id', 'score', 'knowledge_code'])

class Data_Loader(object):
    def __init__(self):
        # 将数据矩阵转化为上述数据格式
        self.data = pd.read_csv('data/data.csv')
        self.Q = pd.read_csv('data/q.csv')
        self.ptr = -1
        self.data_st = defaultdict(list)
        for i in range(self.data.shape[0]):
            for j in range(self.data.shape[1]):
                self.data_st[i].append(Item(j+1, self.data.iloc[i,j], self.Q_item(self.Q, j)))
                #self.data_json.append({'user_id':i+1, 'exer_id':j+1, 'score':data.iloc[i,j], 'knowledge_code':self.Q_item(Q, j)})
        self.knowledge_dim = int(self.Q.shape[1])
        
    def Q_item(self, Q, index):
        tt = []
        n = 0
        for i in Q.iloc[index]:
            n+=1
            if i==1:
                tt.append(n)
        return tt


class DKTModel(nn.Module):

    def __init__(self, topic_size):
        super(DKTModel, self).__init__()
        self.topic_size = topic_size
        # 使用GRU，输入就是【知识点数量*2】，就是前面介绍过的one-hot
        self.rnn = nn.GRU(topic_size * 2, topic_size, 1)
        # 得分预测层
        self.score = nn.Linear(topic_size * 2, 1)

    def forward(self, v, s, h):
        """
            v: 题目知识点的one-hot/muti-hot
            s: 该题得分0/1
            h: 隐藏层(学生状态)
        """
        if h is None:
            h = self.default_hidden()

        v = v.type_as(h)
        score = self.score(torch.cat([h.view(-1), v.view(-1)]))

        x = torch.cat([v.view(-1),
                       (v * (s > 0.5).type_as(v).
                        expand_as(v).type_as(v)).view(-1)])
        _, h = self.rnn(x.view(1, 1, -1), h)
        return score.view(1), h

    def default_hidden(self):
        return torch.zeros(1, 1, self.topic_size)


class DKT(nn.Module):
    def __init__(self, knowledge_n):
        super(DKT, self).__init__()
        self.knowledge_n = knowledge_n
        self.seq_model = DKTModel(self.knowledge_n)
        
    def forward(self, topic, score, hidden=None):
        s, hidden = self.seq_model(topic, score, hidden)
        return s, hidden


def train(data_st, opts):
    knowledge_n = opts['knowledge_n']
    epoch_n = opts['epoch_n']
    
    dkt = DKT(knowledge_n)
    
    optimizer = torch.optim.Adam(dkt.parameters())
    optimizer.zero_grad()
    
    for epoch in range(epoch_n):
        then = time.time()
        total_loss = 0
        total_mae = 0
        total_acc = 0
        total_seq_cnt = 0
    
        students = list(data_st)
        random.shuffle(students)
        student_cnt = len(students)
    
        MSE = torch.nn.MSELoss()
        MAE = torch.nn.L1Loss()
        H = {}
        stu_k_sta = {}
        score_all = {}
        for student in students:
            total_seq_cnt += 1
        
            item_list = data_st[student]
            item_num = len(item_list)
        
            optimizer.zero_grad()
        
            loss = 0
            mae = 0
            acc = 0
            h = None
            score_all[student] = []
            
            for i, item in enumerate(item_list):
                
                #题目的知识点情况
                knowledge = [0.] * knowledge_n  
                for knowledge_code in item.knowledge_code:
                    knowledge[knowledge_code-1] = 1.0
                knowledge = torch.Tensor(knowledge)
                
                score = torch.FloatTensor([float(item.score)])
    
                s, h = dkt(knowledge, score, h)
    
                s = s[0]
        
                loss += F.binary_cross_entropy_with_logits(s, score.view_as(s))
                m = MAE(F.sigmoid(s), score).item()
            
                mae += m
                acc += m < 0.5
                score_all[student].append(s)
                
            H[student] = h
            
            loss /= item_num
            mae /= item_num
            acc = float(acc) / item_num

            total_loss += loss.item()
            total_mae += mae
            total_acc += acc
        
            loss.backward()
            optimizer.step()
        
            now = time.time()
            duration = (now - then) / 60
            if total_seq_cnt%50==0:
                print('[%d:%d/%d] loss %.6f, mae %.6f, acc %.6f' % (epoch, total_seq_cnt, student_cnt,total_loss/total_seq_cnt, total_mae/total_seq_cnt, total_acc/total_seq_cnt))
    return H, score_all


opts = {}
opts['knowledge_n'] = 8
opts['epoch_n'] = 5
data = Data_Loader().data_st
H, score_all = train(data, opts)

编辑于 2022-03-17 20:14