利用RBF神经网络预测腐蚀失重数据—附Matlab代码
MATLAB代码及数据见资源：
https://download.csdn.net/download/weixin_50578602/86733612
一、利用腐蚀动力学曲线拟合来优选数据
已知条件和数据整理如表1、表2所示：
表 1 恶劣环境条件应力的设置
| 试验应力条件 |
温度（K） |
盐度（wt.%） |
湿度 |
| 1# |
308 |
5% |
100% |
| 2# |
323 |
5% |
100% |
| 3# |
323 |
3.5% |
100% |
| 4# |
323 |
2% |
100% |
| 5# |
293 |
5% |
100% |
表 2 实际测量数据（标为绿色的为平均值）
| 时间(h) |
30 |
60 |
120 |
180 |
240 |
300 |
360 |
| 1# |
1.905950 |
3.074790 |
3.970050 |
4.600650 |
5.750750 |
5.947930 |
6.192410 |
| 1.464920 |
2.262560 |
2.275940 |
3.067180 |
3.180960 |
3.964810 |
5.921520 |
|
| 1.685435 |
2.668675 |
3.122995 |
3.833915 |
4.465855 |
4.956370 |
6.056965 |
|
| 2# |
2.082790 |
2.581940 |
2.962170 |
3.957750 |
3.819190 |
1.214620 |
2.353510 |
| 2.153030 |
2.416690 |
2.939280 |
3.774630 |
3.876960 |
4.106810 |
5.071300 |
|
| 2.117910 |
2.499315 |
2.950725 |
3.866190 |
3.848075 |
2.660715 |
3.712405 |
|
| 3# |
3.537250 |
2.473520 |
4.282620 |
3.471800 |
2.709280 |
2.814750 |
3.025350 |
| 1.648720 |
1.809070 |
2.427930 |
3.630870 |
3.461400 |
3.623680 |
3.776890 |
|
| 2.592985 |
2.141295 |
3.355275 |
3.551335 |
3.085340 |
3.219215 |
3.401120 |
|
| 4# |
2.346280 |
2.427460 |
3.272150 |
3.511640 |
2.934970 |
2.912150 |
3.089950 |
| 1.681550 |
2.342690 |
2.277600 |
3.666380 |
3.492370 |
3.663160 |
3.473460 |
|
| 2.013915 |
2.385075 |
2.774875 |
3.589010 |
3.213670 |
3.287655 |
3.281705 |
|
| 5# |
0.939690 |
1.456850 |
2.174910 |
1.810430 |
3.085880 |
2.698200 |
5.593960 |
| 0.772500 |
1.007120 |
2.457830 |
2.358660 |
4.111850 |
3.098350 |
4.191100 |
|
| 0.856095 |
1.231985 |
2.316370 |
2.084545 |
3.598865 |
2.898275 |
4.892530 |
将各环境应力条件下的数据（每个条件下21个数据）导入Matlab软件或者直接读取datafit.m文件，利用Curve Fitting Tool工具箱，以最小二乘法拟合腐蚀失重动力学曲线，拟合类型为自定义模型：
（a、b为待拟合的常数，取95%置信区间的中点）。
结果如下：
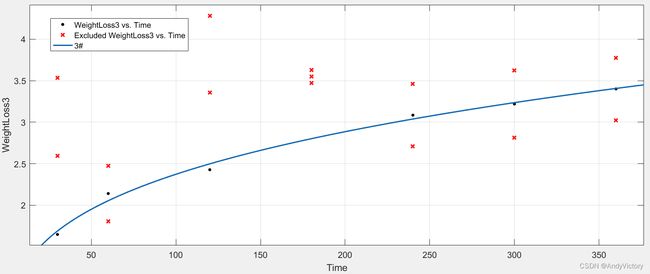
图 1 1#环境应力条件下的腐蚀失重动力学曲线（
）
图1为1#环境应力条件下的腐蚀失重动力学曲线，每个时间点对应两个实测数据和一个平均值。根据和均方根误差RMSE和确定系数R-square的值来对每个时间点的三个数据进行删减，以提高模型的准确性。（图中红色×点表示该点误差较大，不参与动力学曲线拟合）
同理，其他四种环境应力条件下的腐蚀失重动力学曲线如图2到图5所示：
图 2 2#环境应力条件下的腐蚀失重动力学曲线（
）
（30h的数据超出10%误差，预测时以曲线拟合值1.850376替代）
图 3 3#环境应力条件下的腐蚀失重动力学曲线（
）
（180h的数据偏离曲线太多，不参与曲线拟合，预测时以曲线拟合值2.801620替代）
图 4 4#环境应力条件下的腐蚀失重动力学曲线（
）
（180h的数据偏离曲线太多，不参与曲线拟合，预测时以曲线拟合值2.993955替代）
图 5 5#环境应力条件下的腐蚀失重动力学曲线（
）
（120和300h的数据超出10%误差，预测时分别以曲线拟合值1.958366、3.477626替代）
5种环境应力条件的腐蚀失重动力学曲线拟合均方根误差RMSE和确定系数R-square如表3所示。
表 3 曲线拟合优度参数
| RMSE |
R-square |
|
| 1# |
0.1546 |
0.9918 |
| 2# |
0.248 |
0.9454 |
| 3# |
0.06458 |
0.993 |
| 4# |
0.03694 |
0.9967 |
| 5# |
0.2491 |
0.961 |
所有的优选值如表4所示：（红色为曲线拟合时和预测替换的数据，蓝色为只在预测时替换的数据）
表 4 失重数据优选值
| 时间(h) |
30 |
60 |
120 |
180 |
240 |
300 |
360 |
| 1# |
1.464920 |
2.262560 |
3.122995 |
3.833915 |
4.465855 |
4.956370 |
5.921520 |
| 2# |
1.850376 |
2.416690 |
2.962170 |
3.774630 |
3.876960 |
4.106810 |
5.071300 |
| 3# |
1.648720 |
2.141295 |
2.427930 |
2.801620 |
3.085340 |
3.219215 |
3.401120 |
| 4# |
2.013915 |
2.385075 |
2.774875 |
2.993955 |
3.213670 |
3.287655 |
3.473460 |
| 5# |
0.856095 |
1.231985 |
1.958366 |
2.358660 |
3.085880 |
3.477626 |
4.191100 |
二、RBF神经网络简介
2.1 RBF神经网络概述
径向基函数（Radical Basis Function, RBF）是多维空间插值的传统技术，由Powell于1985年提出。
RBF是具有单隐藏层的三层前向网络。第一层输入层：由信号源节点构成，仅起到数据信息的传递作用，对输入信息不做任何变换。第二层隐含层：节点数视需要而定。隐藏层神经元核函数(作用函数)是径向基函数函数，对输入信息进行空间映射的变换。第三层输出层，对输入模式做出响应。输出层神经元的作用函数为线性函数，对隐含层神经元输出的信息进行线性加权后输出，作为整个神经网络的输出结果。
图 6 正则化RBF神经网络拓补图
输出层与隐藏层所完成的任务是不同的，因而他们的学习策略也不同。输出层是对线性权值进行调整，采用的是线性优化策略，因而学习速度较快；而隐藏层是对激活函数（一般取高斯函数）的参数进行调整，采用的是非线性优化策略，因而学习速度较慢。
RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐藏层空间，隐含层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分的问题在高维空间内线性可分。
RBF神经网络结构简单、训练简洁而且学习收敛速度快，能够逼近任意非线性函数，因此它已被广泛应用于时间序列分析、模式识别、非线性控制和图形处理等领域。
2.2 数据点中心计算——聚类算法
本次数据预测采用K-mean聚类算法通过自组织学习来确定数据点中心
位置。这一算法主要基于数据点之间的均值和与聚类中心的距离迭代而成。步骤如下：
- 预先给定聚类的数目同时随机初始化聚类中心；
- 每一个数据点通过计算与聚类中心的欧氏距离来分类到最邻近的一类中；
- 根据分类结果，利用分类后的数据点重新计算聚类中心；
- 重复步骤（2）（3）直到聚类中心不再变化。
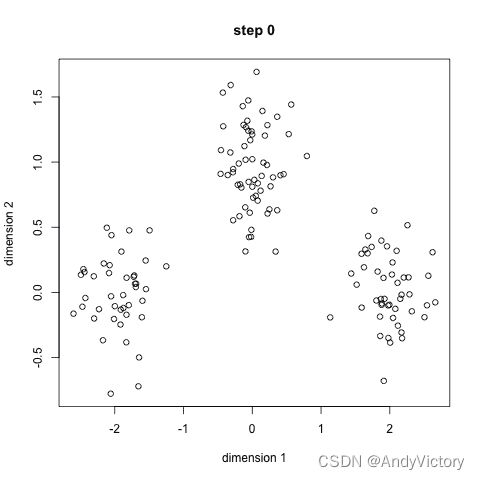
图 7 K-mean算法示意
2.3 隐藏层激活函数——Gauss径向基函数
径向基函数是一个取值仅仅依赖于离原点距离的实值函数（RBF）方法。也就是
。任意一个满足
特性的函数
都叫做径向基函数，标准的一般使用欧式距离（也叫做欧式径向基函数）。最常用的径向基函数是高斯核函数（此外还有反常S型函数、拟多二次函数等），形式为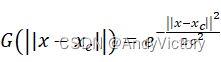
。其中
为核函数中心，σ为函数的宽度参数，控制了函数的径向作用范围。
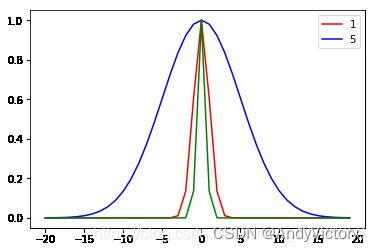
高斯核函数的图像如图8所示，其中横轴是到中心的距离。当距离等于0时，函数值等于1，距离越远衰减越快，其中参数
称为方差（宽度），表示函数跌落到零的速度。红色线条
，蓝色
，绿色
，σ
越小图像越窄。
图 8 高斯径向基函数
2.4 输出层激活函数——线性函数
RBF神经网络输出层的激活函数采用线性函数，即可得到如下方程组：
其中，权重
的值可直接使用梯度下降法训练，通过学习来自适应调节更新。在此不做过多赘述。
2.5 径向基神经网络分类
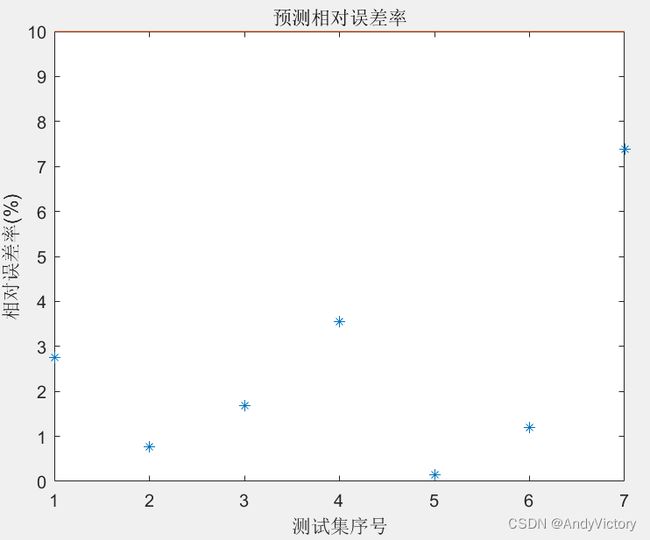
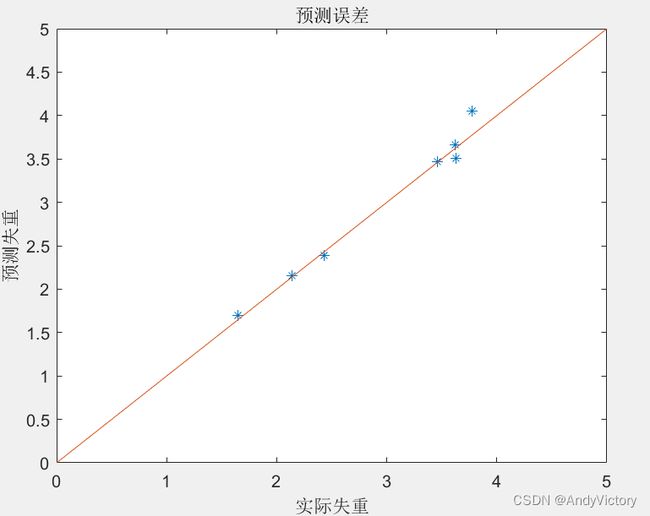
RBF神经网络主要分为两类：正则化径向基函数神经网络和广义径向基神经网络。若设网络具有N个输人节点，P个隐节点，i个输出节点，当N=M 正则化RBF网络具有以下优点： 同时，正则化RBF网络还存在一些问题：一是正则化的RBF要求所有样本对应一个隐层神经元，所带来的问题是计算量很大；二是样本量很大带来的另外一个问题是容易达到病态方程组问题。 因此需要改进RBF神经网络。产生了广义RBF神经网络，但同时广义RBF神经网络也存在一些问题，比如需要调整的参数太多，这些参数通常是通过手动调试，没有特别好的算法进行自动调整。 三、腐蚀失重数据预测 3.1 利用1#、2#、4#、5#的原始数据预测3#数据 利用1#、2#、4#、5#的第二次实测数据（即不通过动力学曲线拟合优选数据的操作）预测3#数据，其中，由于3#条件下60h的实测数据误差过大，使用均值2.141295替代。 经过多次试验，得出如下预测模型及参数选择： 最终得到模型的拟合优度 该模型的MATLAB程序位于1245-3文件夹中。运行结果如下： 表 5 1245-3预测结果 时间（h） 实测数据 预测数据 相对误差率 30 1.64872 1.69423215687772 0.0276 60 2.141295 2.15787081480126 0.0077 120 2.42793 2.38723358080473 0.0168 180 3.63087 3.50227753435955 0.0354 240 3.4614 3.46634152765546 0.0014 300 3.62368 3.66719813655521 0.0120 360 3.77689 4.05563087419860 0.0738 图 9 1245-3预测相对误差率 图 10 1245-3训练误差 图 11 1245-3预测误差 3.2 利用1775组拓展数据预测5种条件下的360h数据 每个条件下的时间取1、2、3、…、355h，代入通过动力学曲线拟合优选数据得到的拟合函数，这样一共得到 经过多次试验，得出如下预测模型及参数选择： 最终得到模型的拟合优度 该模型的MATLAB程序位于1245-3文件夹中。运行结果如下（由于本模型采用正则化径向基函数神经网络，故训练误差为0）： 表 6 1775-5预测结果 实测数据 预测数据 相对误差率 1# 5.92152 5.66621330245471 0.0431 2# 5.0713 4.61953571303820 0.0891 3# 3.40112 3.36350038512683 0.0111 4# 3.47346 3.40976860984301 0.0183 5# 4.1911 3.87746849521136 0.0748 图 12 1775-5预测相对误差率 图 13 1775-5预测误差（红色范围为±10%误差）
，总可以找到一组权值使得正则化网络对于
的逼近优于所有其可能的选择。
=0.9813，预测数据的平均相对误差率为0.0250。
组数据，用这些拓展数据来预测5种条件下的360h数据。（数据点的替换及取舍在第一章中有详细说明）
0.9829，预测数据的平均相对误差率为0.0473。
