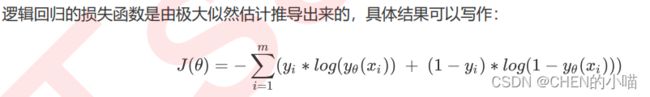sklearn-逻辑回归

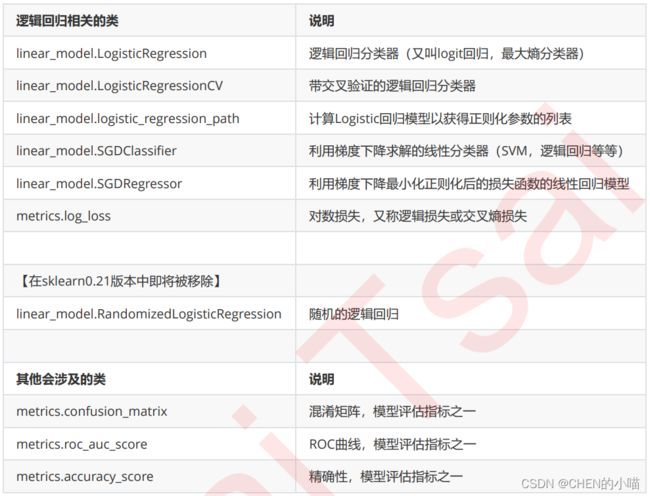
1 sklearn中的逻辑回归

linear_model.LogisticRegression

class sklearn.linear_model.LogisticRegression (penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100, multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)

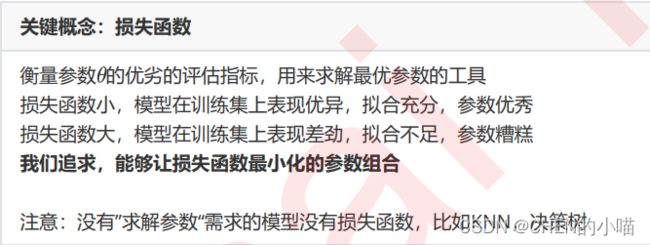
2 损失函数的概念

我们使用”损失函数“这个评估指标，来衡量参数为 的模型拟合训练集时产生的信息损失的大小，并以此衡 量参数 的优劣。如果用一组参数建模后，模型在训练集上表现良好，那我们就说模型拟合过程中的损失很小，损 失函数的值很小，这一组参数就优秀；相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不 足，效果较差，这一组参数也就比较差。即是说，我们在求解参数 时，追求损失函数最小，让模型在训练数据上 的拟合效果最优，即预测准确率尽量靠近100%。

 其中， 表示求解出来的一组参数，m是样本的个数， 是样本i上真实的标签， 是样本i上，基于参数 计算 出来的逻辑回归返回值， 是样本i各个特征的取值。我们的目标，就是求解出使 最小的 取值。对逻辑回归中过拟合的控制，通过正则化来实现

3 重要参数penalty & C

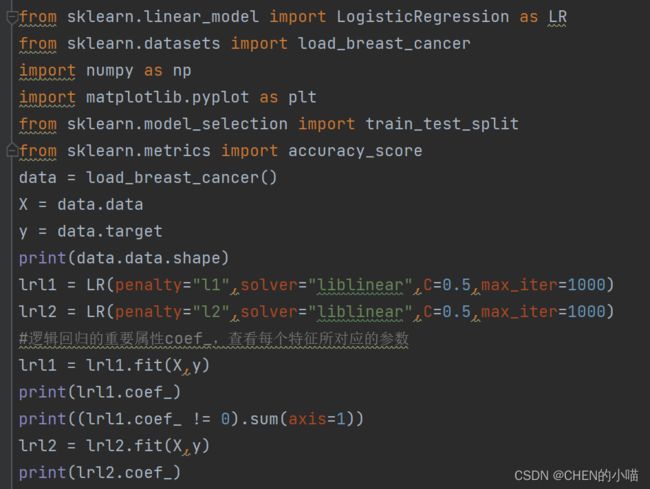
正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向量 的L1范式和L2范式的倍数来实现。这个增加的范式，被称为“正则项”，也被称为"惩罚项"。损失函数改变，基于损失函数的最优化来求解的参数取值必然改变，我们以此来调节模型拟合的程度。其中L1范式表现为参数向量中的每个参数的绝对值之和，L2范数表现为参数向量中的每个参数的平方和的开方值。

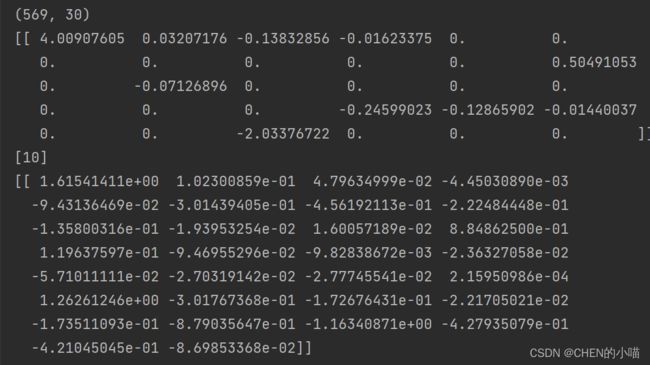
 L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小）， 参数 的取值会逐渐变小，但L1正则化会将参数压缩为0，L2正则化只会让参数尽量小，不会取到0。

如果 特征量很大，数据维度很高，我们会倾向于使用L1正则化。由于L1正则化的这个性质，逻辑回归的特征选择可以由 Embedded嵌入法来完成。

相对的，L2正则化在加强的过程中，会尽量让每个特征对模型都有一些小的贡献，但携带信息少，对模型贡献不大 的特征的参数会非常接近于0。通常来说，如果我们的主要目的只是为了防止过拟合，选择L2正则化就足够了。但 是如果选择L2正则化后还是过拟合，模型在未知数据集上的效果表现很差，就可以考虑L1正则化。 而两种正则化下C的取值，都可以通过学习曲线来进行调整。

输出：

 当我们选择L1正则化的时候，许多特征的参数都被设置为了0，这些特征在真正建模的时候，就不会出 现在我们的模型当中了，而L2正则化则是对所有的特征都给出了参数。

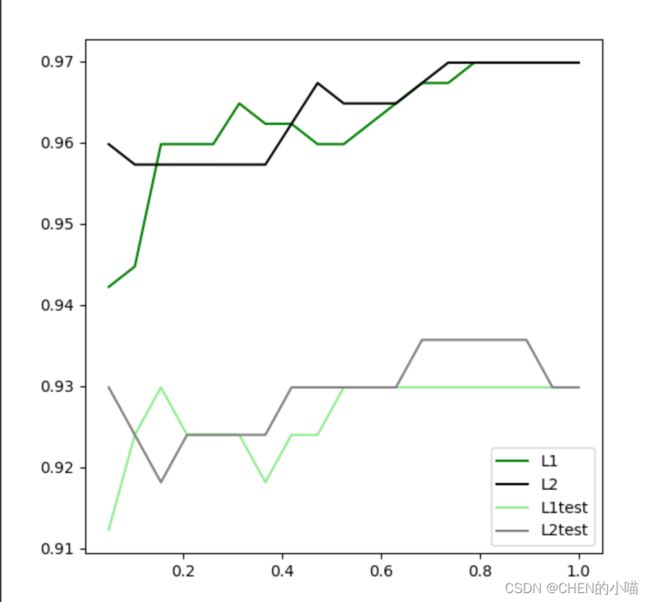
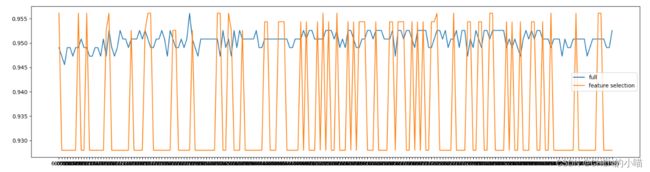
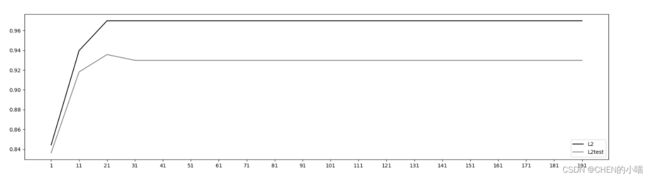
比较l1正则化和l2正则化随着c的逐渐增大，分别在测试集和训练集上的效果

 

 但随着C的逐渐变大，正则化的强度越来越 小，模型在训练集和测试集上的表现都呈上升趋势，直到C=0.8左右，训练集上的表现依然在走高，但模型在未知 数据集上的表现开始下跌，这时候就是出现了过拟合。我们可以认为，C设定为0.8会比较好。在实际使用时，基本就默认使用l2正则化，如果感觉到模型的效果不好，那就换L1试试看。

4 逻辑回归中的特征工程

高效的嵌入法embedded

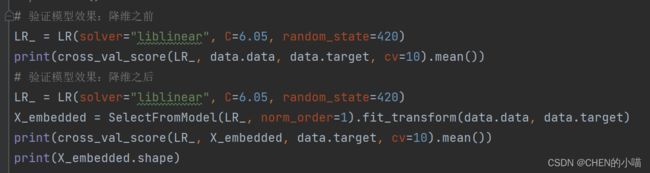
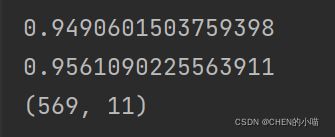
由于L1正则化会使得部分特征对应 的参数为0，因此L1正则化可以用来做特征选择，结合嵌入法的模块SelectFromModel，我们可以很容易就筛选出 让模型十分高效的特征。注意，此时我们的目的是，尽量保留原数据上的信息，让模型在降维后的数据上的拟合效 果保持优秀，因此我们不考虑训练集测试集的问题，把所有的数据都放入模型进行降维。

 

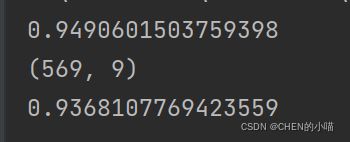
结果，特征数量被减小到个位数，并且模型的效果却没有下降太多，但是，能否让模型的拟合效果更好呢？在这里，我们有两种调整方式：

（1）调节SelectFromModel这个类中的参数threshold，这是嵌入法的阈值，表示删除所有参数的绝对值低于这个阈 值的特征。

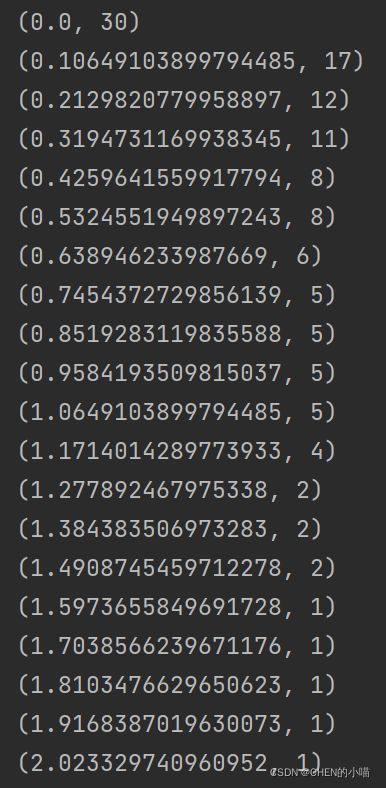
现在threshold默认为None，所以SelectFromModel只根据L1正则化的结果来选择了特征，即选择了所 有L1正则化后参数不为0的特征。我们此时，只要调整threshold的值（画出threshold的学习曲线），就可以观察 不同的threshold下模型的效果如何变化。一旦调整threshold，就不是在使用L1正则化选择特征，而是使用模型的 属性.coef_中生成的各个特征的系数来选择。coef_虽然返回的是特征的系数，但是系数的大小和决策树中的 feature_ importances_以及降维算法中的可解释性方差explained_vairance_概念相似，其实都是衡量特征的重要 程度和贡献度的，因此SelectFromModel中的参数threshold可以设置为coef_的阈值，即可以剔除系数小于 threshold中输入的数字的所有特征。

输出：

 

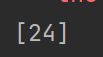
 当threshold越来越大，被删除的特征越来越 多，模型的效果也越来越差，模型效果最好的情况下需要保证有17个以上的特征。实际上我画了细化的学习曲线， 如果要保证模型的效果比降维前更好，我们需要保留25个特征，这对于现实情况来说，是一种无效的降维

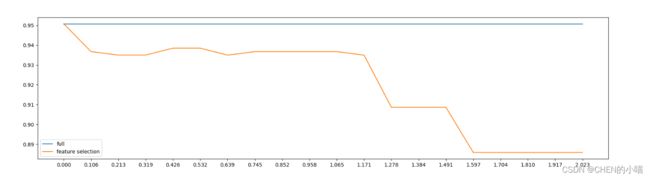
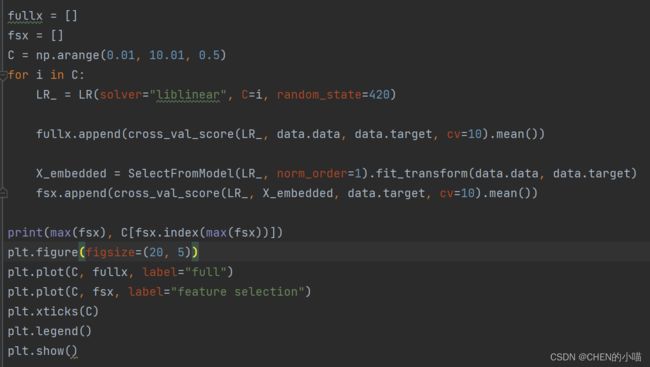
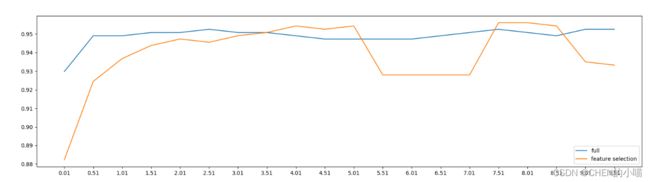
（2）第二种调整方法，是调逻辑回归的类LR_，通过画C的学习曲线来实现

 

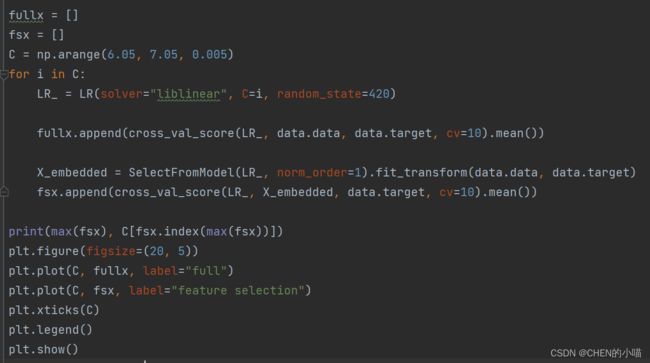
 效果最好时C的取值为7.51，继续细化学习曲线

 验证模型效果

 

 5 梯度下降：重要参数max_iter

逻辑回归的数学目的是求解能够让模型最优化，拟合程度最好的参数 的值，即求解能够让损失函数 最小化的 值。对于二元逻辑回归来说，有多种方法可以用来求解参数 ，最常见的有梯度下降法(Gradient Descent)，坐标下 降法(Coordinate Descent)，牛顿法(Newton-Raphson method)等，其中又以梯度下降法最为著名。人为设置的100次滚动限制，就是sklearn中逻辑回归的参数max_iter，代表着能走的最大步 数，即最大迭代次数。

 使用属性.n_iter_来调用本次求解中真正实现的迭代次数

 

6  二元回归与多元回归：重要参数solver & multi_class

之前我们对逻辑回归的讨论，都是针对二分类的逻辑回归展开，其实sklearn提供了多种可以使用逻辑回归处理多 分类问题的选项。比如说，我们可以把某种分类类型都看作1，其余的分类类型都为0值，和”数据预处理“中的二值 化的思维类似，这种方法被称为"一对多"(One-vs-rest)，简称OvR，在sklearn中表示为“ovr"。又或者，我们可以把 好几个分类类型划为1，剩下的几个分类类型划为0值，这是一种”多对多“(Many-vs-Many)的方法，简称MvM，在 sklearn中表示为"Multinominal"。每种方式都配合L1或L2正则项来使用。 在sklearn中，我们使用参数multi_class来告诉模型，我们的预测标签是什么样的类型。

multi_class 输入"ovr", "multinomial", "auto"来告知模型，我们要处理的分类问题的类型。默认是"ovr"。

'ovr':表示分类问题是二分类，或让模型使用"一对多"的形式来处理多分类问题。

'multinomial'：表示处理多分类问题，这种输入在参数solver是'liblinear'时不可用。

"auto"：表示会根据数据的分类情况和其他参数来确定模型要处理的分类问题的类型。比如说，如果数据是二分 类，或者solver的取值为"liblinear"，"auto"会默认选择"ovr"。反之，则会选择"nultinomial"。

注意：默认值将在0.22版本中从"ovr"更改为"auto"。

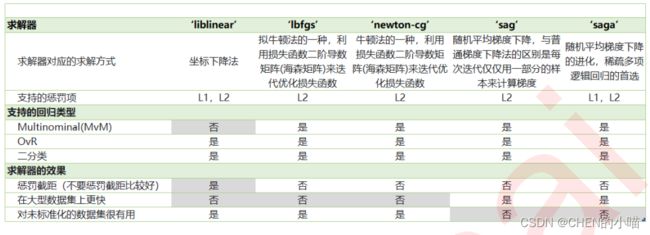
我们之前提到的梯度下降法，只是求解逻辑回归参数 的一种方法，并且我们只讲解了求解二分类变量的参数时的 各种原理。sklearn为我们提供了多种选择，让我们可以使用不同的求解器来计算逻辑回归。求解器的选择，由参 数"solver"控制，共有五种选择。其中“liblinear”是二分类专用，也是现在的默认求解器。

来看看鸢尾花数据集上，multinomial和ovr的区别怎么样：