MatLab矩阵

矩阵：在数学上，定义m×n个数(i=1, 2…, m ; j=1, 2,… n)排成的m行n列的数表示为m行n列的矩阵，并且用大写加粗黑色字母表示。

矩阵创建

直接创建

将矩阵的元素用中括号[]括起来，按矩阵行的顺序输入各元素，同行的各元素之间用逗号,或空格分隔，不同行的元素之间用分号;分隔。

>> a = [1,2,3;4 5 6;7 8 9]
a =
     1     2     3
     4     5     6
     7     8     9

矩阵拼接（串联）

串联是连接数组以便形成更大数组的过程。成对的方括号 [] 即为串联运算符。
使用逗号(,)将彼此相邻的数组串联起来称为水平串联。每个数组必须具有相同的行数。

>> A = [a,a]
ans =
     1     2     3     1     2     3
     4     5     6     4     5     6
     7     8    10     7     8    10

如果各数组具有相同的列数，则可以使用分号(;)垂直串联

>> A = [a; a]
ans =
     1     2     3
     4     5     6
     7     8    10
     1     2     3
     4     5     6
     7     8    10

冒号表达式

使用冒号运算符较通用的格式 start(初始值):step(步长):end(终止值) 创建等距向量值。包含初始值和终止值

>> B = 0:10:100
B =

     0    10    20    30    40    50    60    70    80    90   100

如果省略中间的步骤（如 start:end 中），MATLAB 会使用默认步长值 1。

>> B = 0:10
B =

     0     1     2     3     4     5     6     7     8     9    10

>> a = 8:5:10
a =
     8

行矩阵–linspace

linspace 类似于冒号运算符“:”，但可以直接控制点数并始终包括端点。“linspace”名称中的“lin”指示生成线性间距值而不是同级函数 logspace，后者会生成对数间距值。会有小数

% 语法
linspace(start, last, num)
% 首个元素，最后元素，元素总数
% 生成 n 个点。这些点的间距为 (x2-x1)/(n-1)。

linspace(start,last)
% 当 num 省略时，返回包含 x1 和 x2 之间的 100 个等间距点的行向量。

>> linspace(1,9,10)
ans =
    1.0000    1.8889    2.7778    3.6667    4.5556    5.4444    6.3333    7.2222    8.1111    9.0000

logspace(a, b, n) 在区间 [10^a, 10^b]生成 n 个点，n默认为50

代码表示：dVec = [$10^0$​, $10^{0.01}$​, $10^{0.02}$​, ……, $10^{0.99}$​, $10^1$​​​]

dVec = logspace(0, 1, 101)  

复数矩阵

虚数单位(i)是 -1 的平方根($i^2$= -1)
复数包含实部和虚部，虚数单位(i)是 -1 的平方根($i^2$ = -1)

>> sqrt(-1)
ans = 0.0000 + 1.0000i

要表示复数的虚部，请使用 i 或 j。

c = [3+4i, 4+3j; -i, 10j]

   3.0000 + 4.0000i   4.0000 + 3.0000i
   0.0000 - 1.0000i   0.0000 +10.0000i

>> B = [1 2 3;4 5 6];
>> C = [6,7,8;9,10,11];
>> A = B + i*C
A =
   1.0000 + 6.0000i   2.0000 + 7.0000i   3.0000 + 8.0000i
   4.0000 + 9.0000i   5.0000 +10.0000i   6.0000 +11.0000i

利用函数创建矩阵

利用MATLAB内部函数与工具箱函数产生矩阵
eye(m,n)	m*n阶单位矩阵
ones(m,n)	m*n阶全为1的矩阵
zeros(m,n)	m*n阶全为0的矩阵
magic(n)	n阶魔方(幻方)矩阵
rand(m,n)	[0,1]之间均匀分布的随机矩阵
randn(m,n)	均值为0、方差为1的标准正态分布的随机矩阵
vander([a b c])	以a,b,c为基础元素的范德蒙德(Vandermonde)矩阵
diag([a b c]) diag([a,b,c])	以a,b,c为对角线上的元素的对角矩阵

n阶幻方矩阵指的是将1,2,3,…n²这n²填入矩阵
每行的和，每列的和，两条对角线的和均相等。

% 1，8，6作为矩阵第二列的元素，纵向
fliplr(vander([1,8,6]))
ans =
     1     1     1
     1     8    64
     1     6    36
  
>> diag([1,2])
ans =
     1     0
     0     2

矩阵索引

MATLAB中的每个变量都是一个可包含许多数字的矩阵。如果要访问矩阵的选定元素，请使用索引。

  以 4×4 幻方矩阵 A 为例：

n阶幻方矩阵指的是将1,2,3,…n²这n²填入矩阵
每行的和，每列的和，两条对角线的和均相等。

>> A = magic(4)
A =
    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

引用矩阵元素

KaTeX parse error: Undefined control sequence: \matrix at position 10: \left[ \̲m̲a̲t̲r̲i̲x̲{ 1_{(1,1)}…

下标为正整数、用小括号()括起

方法1:指定行、列下标

>> A(2,2)
ans = 5

方法2:通过序号来引用

在MATLAB中，矩阵元素按列存储，即首先存储矩阵的第一列元素，然后存储第二列元素，…，一直到矩阵的最后一列元素。 矩阵元素的序号就是矩阵元素在内存中的排列顺序。

>> A(4)
ans = 4

>> A(8)
ans = 8

使用单一下标引用数组中特定元素的方法称为线性索引。

序号与下标是一一对应的，以m*n矩阵A为例，矩阵元素A(i,j)的序号为(j-1)*m+i

% 思考
A=[1,2,3;4,5,6]
A(3) = ?

序号与下标的转换

sub2ind函数：将矩阵中指定元素的行、列下标转换成存储的序号

D = sub2ind(S,I,J)
% D：对应于下标元素的序号，其行列数与I、J相同
% S：由行数和列数两个元素组成的向量,用size()获取
% I：转换矩阵的行下标
% J：转换矩阵的列下标
% 如果i、j是矩阵的话，表示要将矩阵中的多个元素的行列下标转换成存储的序号，那么I、J的行列数必须相等

>> A=[1:3;4:6]
A =
     1     2     3
     4     5     6
>> D=sub2ind(size(A),[1,2;2,2],[1,1;3,2])
D =
     1     2
     6     4
>> A(D)
ans =
     1     4
     6     5

>> A=rand(5)
A =
    0.7060    0.8235    0.4387    0.4898    0.2760
    0.0318    0.6948    0.3816    0.4456    0.6797
    0.2769    0.3171    0.7655    0.6463    0.6551
    0.0462    0.9502    0.7952    0.7094    0.1626
    0.0971    0.0344    0.1869    0.7547    0.1190

% 即我们输入的坐标（1,2），（2,3），（3,4）在矩阵A中的索引号，意思是A矩阵第1行第2个元素的索引值号为6，为什么是6呢？因为MATLAB是按列搜索的。同理A中的第2行第3个的索引号为12，后面依次类推。
>> b=sub2ind(size(A),[1 2 3],[2 3 4])
b =
     6    12    18
     
% 如何取出A中（1,2），（2,3），（3,4）
>> A(b)
ans =
    0.8235    0.3816    0.6463

ind2sub函数:将把矩阵元素的序号转换成对应的下标

[I,J] = ind2sub(S,D)
% I：矩阵的行下标
% J：矩阵的列下标
% S：行数和列数组成的向量
% D：序号

>> [I,J]=ind2sub([3,3],[1,3,5])
I =
     1     3     2
J =
     1     1     2

批量引用

要引用多个数组元素，请使用冒号运算符，这使您可以指定一个格式为 start:end 的范围。

% 例如，列出 A 前三行及第二列中的元素：
>> A = magic(3)
>> A(1:3,2)
ans =
     2
    11
     7

单独的冒号（没有起始值或结束值）指定该维中的所有元素。例如，选择 A 第三行中的所有列：

>> A(3, :)
ans =
     4     9     2

end运算符

表示某一维的末尾元素下标。

>> A = [1:5;6:10;11:15;16:20];
% 引用最后一列元素
>> A(:,end)
ans =
     5
    10
    15
    20
% 引用最后一行元素
>> A(end,:)
ans =
    16    17    18    19    20
    
% 引用第一行和第四行，从第3列到最后一列的元素,包括边界的行或列
>> A([1,4],3:end)
ans =
     3     4     5
    18    19    20

表达式(Matlab程序)	函数功能
A(1)	将二维矩阵A重组为一维数组，返回数组中第一个元素
A(: , j)	返回二维矩阵A中第 j 列 列向量
A( i , : )	返回二维矩阵A中第 i 行 行向量
A(: , j : k)	返回二维矩阵A中第 j 列到第 k列 列向量组成的子矩阵
A( i : k , : )	返回二维矩阵A中第 i 行到第 k行 行向量组成的子矩阵
A( i : k , j : m)	返回二维矩阵A中第 i 行到第 k 行 行向量和第 j 列到第 m 列 列向量的交集组成的子矩阵
A(: )	将二维矩阵A中得每列合并成一个列向量，类似于reshape()函数
A( j : k)	返回一个行向量，其元素为A(:)中的第 j 个元素到第 k 个元素
A([ j1 j2…])	返回一个行向量，其元素为A(:)中的第 j1，j2…个元素
A(: , [ j1 j2 …])	返回矩阵A的第 j1 列、第 j2 列等的列向量
A([ i1 i2 …] : ,)	返回矩阵A的第 i1 行、第 i2 行等的行向量
A([ i1 i2 …] , [ j1 j2 …])	返回矩阵A的第 j1列、第 j2 列等和矩阵A的第 i1 行、第 i2 行等的元素

数组越界

如果尝试引用数组（矩阵）外部元素，MATLAB就 会引发错误。

>> test = A(4,5)
Index exceeds matrix dimensions.

矩阵扩大

MATLAB提供了三种方法来实现这一功能：连接操作符[ ]、阵列连接函数cat和重复函数repmat。像分块矩阵构造大矩阵一样，通过连接操作符[ ]将小矩阵连接成大矩阵。

>> a = [1 2;3 4];
>> b = [5 6;7 8];
% 矩阵左右合并
>> [a b];
>> [a,b];
>> horzcat[a,b];
ans =
     1     2     5     6
     3     4     7     8
% 矩阵上下合并
>> [a;b];
>> vertcat[a,b];
ans =
     1     2
     3     4
     5     6
     7     8

如果引用的行列下标大于原矩阵的行数和列数，那么matlab将自动扩展原矩阵，并将扩展后未赋值的元素置为0

>> A(4,5) = 17

    16     2     3    13     0
     5    11    10     8     0
     9     7     6    12     0
     4    14    15     1    17

---

矩阵缩小

将大矩阵发成小矩阵的方法有两种：抽取法和删除法。
抽取法是指从大的矩阵中抽取其中的一部分，从而构成新的矩阵；
删除法是在原来矩阵中，利用空矩阵[]删除指定的行或列。

>> a = [1:5;6:10;11:15]
a =
     1     2     3     4     5
     6     7     8     9    10
    11    12    13    14    15
% 返回矩阵a的第2列到第4列列向量组成的子矩阵
>> b = a(:,2:4)
b =
     2     3     4
     7     8     9
    12    13    14
% 返回矩阵b第二行，令第二行元素为空
>> b(2,:) = []
b =
     2     3     4
    12    13    14

---

矩阵变换

函数	作用
rot90(M)	使矩阵M逆时针旋转90。
tril(M)	提取矩阵的下三角矩阵
triu(M)	提取矩阵的上三角矩阵
fliplr(M)	将矩阵M左右翻转，以矩阵中间一列为轴，左右元素交换位置 left-right
flipud(M)	将矩阵M上下翻转，以矩阵中间一行为轴，左右元素交换位置 up-down
reshape(A,m,n)	在矩阵总元素保持不变的前提下，将矩阵A重新排成m×n的二维矩阵。 注意：reshape函数只是改变原矩阵的行数和列数，但并不改变原矩阵元素个数及其存储顺序。

>> a
a =
     1     2     3
     4     5     6
>> triu(a)
ans =
     1     2     3
     0     5     6
     
>>  x=[23,45,65,34,65,34,98,45,78,65,43,76]; 
>> reshape(x,3,4)
ans =
    23    34    98    65
    45    65    45    43
    65    34    78    76

---

矩阵转置

矩阵的转置用符号'来表示

M'和M.'：对于实数来说都是转置，效果相同
M'：在复数矩阵的转置中，不是矩阵元素进行转置，而是元素转为其共轭复数
M.'：在复数矩阵中仍是转置。

如果需要对矩阵转置，使用.'更可靠

>> a = [1 4 5;8 9 5;8 5 5]

>> b = a'
b =
     1     8     8
     4     9     5
     5     5     5
>> c = [1 4 5;8 9 5;8 5 5]'
c =
     1     8     8
     4     9     5
     5     5     5

>> a = [1 2;3 4]
a =
     1     2
     3     4
>> a'
ans =
     1     3
     2     4
>> a.'
ans =
     1     3
     2     4
	 
>> b=[1+2i,3-4i;5+6i,7];

>> b'

ans =
  1.0000 - 2.0000i   5.0000 - 6.0000i

  3.0000 + 4.0000i  7.0000         

>> b.'

ans =
  1.0000 + 2.0000i   5.0000 + 6.0000i

  3.0000 - 4.0000i   7.0000	 

Matlab中的共轭转置、共轭及转置

% 随机产生的一个复数矩阵
>> a = randn(2,2) + randn(2,2)*1i
a =
  -0.2050 + 1.4172i   1.4897 - 1.2075i
  -0.1241 + 0.6715i   1.4090 + 0.7172i
  
% 共轭
>> conj(a)
ans =
  -0.2050 - 1.4172i   1.4897 + 1.2075i
  -0.1241 - 0.6715i   1.4090 - 0.7172i
  
% 转置
>> a.'
ans =
  -0.2050 + 1.4172i  -0.1241 + 0.6715i
   1.4897 - 1.2075i   1.4090 + 0.7172i
   
% 共轭转置--1
>> conj(a.')
ans =
  -0.2050 - 1.4172i  -0.1241 - 0.6715i
   1.4897 + 1.2075i   1.4090 - 0.7172i
% 共轭转置--2
>> conj(a).'
ans =
  -0.2050 - 1.4172i  -0.1241 - 0.6715i
   1.4897 + 1.2075i   1.4090 - 0.7172i
   
% 埃尔米特转置运算符，进行转置和共轭，结果一致；
% 如果进行操作的数是实数，直接使用这个符号，共轭的作用就消失了，类似与转置
>> a'
ans =
  -0.2050 - 1.4172i  -0.1241 - 0.6715i
   1.4897 + 1.2075i   1.4090 - 0.7172i

---

矩阵计算

矩阵计算	作用
size(M)	返回矩阵M的大小
det(M)	计算方阵M的行列式
rank(M)	返回矩阵M的秩
trace(M)	返回矩阵M的迹
inv(M)	输出方阵M的逆矩阵
pinv(M)	输出矩阵M的伪逆矩阵
rref(M)	返回矩阵M的行最简形矩阵
poly(M)	输出向量或方阵M的特征多项式
[vec,val]=eig(M)	输出方阵M的特征值和特征向量
orth(M)	输出矩阵M的正交矩阵

矩阵运算

MATLAB允许使用单一的算术运算符或函数来处理矩阵中的所有值。

>> a = [1 1 1;2 1 3;1 1 4];
>> a + 10
ans =
    11    11    11
    12    11    13
    11    11    14
>> sin(a)
ans =
    0.8415    0.8415    0.8415
    0.9093    0.8415    0.1411
    0.8415    0.8415   -0.7568

* 运算符执行矩阵乘法。前一矩阵的列数和后一矩阵的行数相同

% 例如，确认矩阵乘以其逆矩阵可返回单位矩阵：
>> p = a * inv(a)
p =
    1.0000         0         0
         0    1.0000         0
    0.0000         0    1.0000

矩阵数乘

>> A = [1 2 3;4 5 6];
>> B = 3*A
B =
     3     6     9
    12    15    18

方阵的行列式

>> a = [1 1 1;2 1 3;1 1 4];
>> det(a)
ans =
    -3

矩阵求逆

非奇异矩阵A求逆用inv(A)表示

非奇异(非退化、满秩)矩阵：方阵A的行列式|A|~=0，可求其逆

>> a = [1 1 1;2 1 3;1 1 4];
>> inv(a)
ans =
   -0.3333    1.0000   -0.6667
    1.6667   -1.0000    0.3333
   -0.3333         0    0.3333
% 验证正确与否，结果为单位矩阵则正确
>> p = a * inv(a);

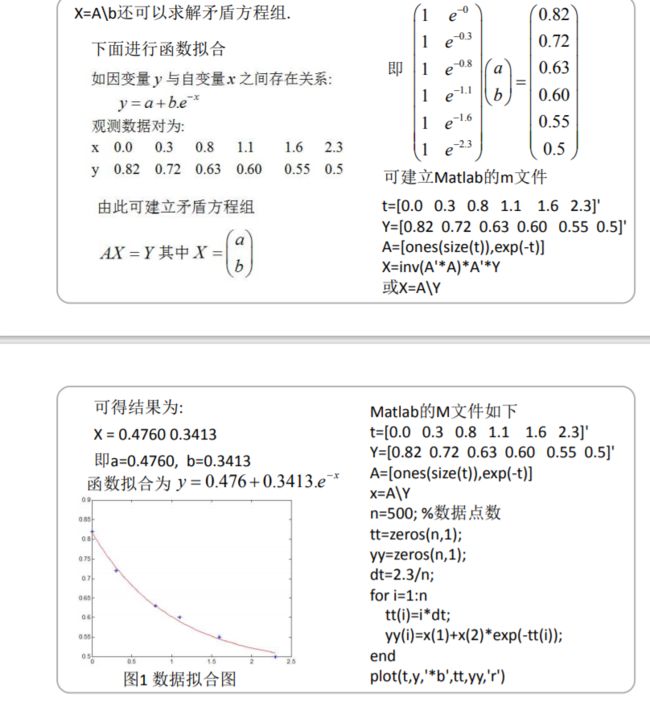
% 利用逆矩阵可以解方程组. 如AX=b
A=[1 3 6;2 5 8;3 9 11]
b=[3 6 7]’
% 计算表达式为X=inv(A)*b
% 结果为:
X = 4.7143
-1.1429
0.2857
% 或用X=A\b也可求解.

矩阵特征值与特征向量

如果A为方阵，满足AX = λX的λ称为A的特征值，X称为A的特征向量。计算A的特征值用eig(A)表示。

>> A = [1 3 6; 2 5 8; 3 6 8]; 
>> Z = eig(A)
Z =
   15.2382
   -1.3365
    0.0982
% vec各列为特征向量
% val主对角元素为特征值
>> [vec,val]=eig(A)
vec =
   -0.4135   -0.7851    0.7318
   -0.6094   -0.3748   -0.6472
   -0.6765    0.4931    0.2136
val =
   15.2382         0         0
         0   -1.3365         0
         0         0    0.0982

format

上述的a * inv(a)中小数点后出现的0。请注意，p 不是整数值矩阵。MATLAB 将数字存储为浮点值，算术运算可以区分实际值与其浮点表示之间的细微差别。使用 format 命令可以显示更多小数位数：

>> format long
>> p = a*inv(a)

   1.000000000000000                   0                   0
   0.000000000000002   1.000000000000000                   0
   0.000000000000002  -0.000000000000004   1.000000000000000

使用以下命令将显示内容重置为更短格式

>> format short

format 仅影响数字显示，而不影响 MATLAB 对数字的计算或保存方式。

矩阵元素级运算

矩阵元素之间的运算

元素级乘法，请使用 .* 运算符：

>> p = a.*a

     1     4     9
    16    25    36
    49    64   100

乘法、除法和幂的矩阵运算符分别具有执行元素级运算的对应数组运算符。例如，计算 a 的各个元素的三次方：

>> a.^3

           1           8          27
          64         125         216
         343         512        1000

结构、单元数组

单元数组和结构数组是一种新的数据类型，能将不同类型、不同维数的数组组合在一起，从而方便对不同的数据类型方便管理和维护。

结构矩阵(TO DO)

把数据类型不同而逻辑上相关的数据组成一个有机整体，其中每个数据就构成了这个结构数据的一个成员，例如：学生包含了三个成员，学号、姓名、性别。结构矩阵中的元素就是结构数据类型

由结构数据构成的矩阵就是结构矩阵 结构矩阵 里 的 每个 元素就是 结构数据类型 。

% 格式为：
结构矩阵元素.成员名 = 表达式

a(1).x1=10; a(1).x2='liu'; a(1).x3=[11,21;34,78];
a(2).x1=12; a(2).x2='wang'; a(2).x3=[34,191;27,578];
a(3).x1=14; a(3).x2='cai'; a(3).x3=[13,890;67,231];

单元数组（细胞数组）

单元矩阵定义方法与普通矩阵类似，但定义时用大括号 { }括起

使用时类似普通矩阵，直接调用单元内容即可：

>> b = {11,'abc',[1 2 3] ...
22,'def',[4 5 6] ...
33,'ijk',[7 8 9]}
b =
  1×9 cell 数组
   {[11]}    {'abc'}    {1×3 double}    {[22]}    {'def'}    {1×3 double}    {[33]}    {'ijk'}    {1×3 double}
>> b(1,6)
ans =
  1×1 cell 数组
    {1×3 double}
>> b(1,5)
ans =
  1×1 cell 数组
    {'def'}

操作矩阵的函数

下面对矩阵
$A=⎡⎣107250369⎤⎦A=\left[\begin{array}{ccc}1& 2& 3\\ 0& 5& 6\\ 7& 0& 9\end{array}\right]\ast A\ast =⎣⎡107250369⎦⎤$

进行操作以演示操作矩阵的常见函数

函数	作用	例子	结果
max(A, [], dim)	获取矩阵A的dim维度上的最大值	max(A, [], 1)	$\left[\begin{array}{ccc}7& 5& 9\end{array}\right]$
min(A, [], dim)	获取矩阵A的dim维度上的最小值	min(A, [], 2)	$\left[\begin{array}{ccc}1& 0& 0\end{array}\right]$
sum(A, dim)	获取矩阵A的dim维度上的和	sum(A, 1)	$\left[\begin{array}{ccc}8& 7& 18\end{array}\right]$
mean(A, dim)	获取矩阵A的dim维度上的平均值	mean(A, 1)	$\left[\begin{array}{ccc}2.6667& 2.3333& 6.0000\end{array}\right]$
sort(A, dim, direction)	获取矩阵A的dim维度上按direction顺序排序结果	sort(A, 1, 'descend')	$\left[\begin{array}{ccc}7& 5& 9\\ 1& 2& 6\\ 0& 0& 3\end{array}\right]$
sortrows(A, column)	获取矩阵A按照每行第column个元素升序排序结果.	sortrows(A, 2)	$\left[\begin{array}{ccc}7& 0& 9\\ 1& 2& 3\\ 0& 5& 6\end{array}\right]$
size(A, dim)	获取矩阵A的dim维度上的形状.若不指定dim,则返回整个矩阵的形状.	size(A)	$\left[\begin{array}{cc}3& 3\end{array}\right]$
find(A, n)	获取矩阵A前n个非零元素的索引	find(A,5)	$\left[\begin{array}{ccccc}1& 3& 4& 5& 7\end{array}\right]$

对于上面这些函数,除第一个参数以外,其它参数都是可选的.