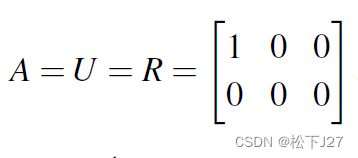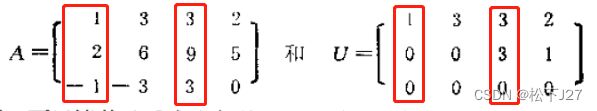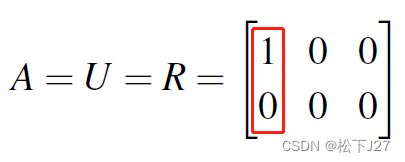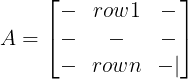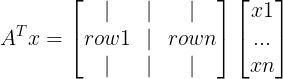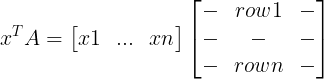线性代数 --- 线性代数基本定理上（四个基本子空间的维数，行秩=列秩）
由向量张成VS用条件约束
构造子空间的方法主要有两种：
1，一种是给出一组向量，由他们来张成子空间。
例如，矩阵的列空间和行空间就是通过这种方法来构造的。
2，一种是给出子空间所应受到的约束，满足这些约束条件的向量构成了该子空间。
例如，矩阵的零空间，就是由满足齐次方程组Ax=0的解构成的，方程组Ax=0中的每一个方程都是一个约束条件。
对于第一种方法而言，可以有多余的向量，即，线性相关的向量。对于第二种方法而言也可以有多余的约束条件。
"下面我们逐一讨论四个基本子空间，并讨论基底的求法。我们指出，这四个基本子空间都与矩阵U有关系，我们的问题是找出他们与原矩阵A的关系。"(打引号的这句话，不仅仅是原作者的重点，也是本文的重点。)
A的行空间与零空间都是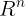
的子空间
1，A的行空间
,C for Column --- 由向量张成
补充，上文中所提到的2L，所强调的应该是文中的第二句：
如何构造行空间：
A的行空间包含了U的行空间，是用阶梯矩阵U中的r个非零行作为基底去张成的。（注：不同的消元方式可能会产生不同的U矩阵，但不论用什么消元法，最终产生的U矩阵中的r个非零行，都可以作为A的行空间的基底，因为，基底不唯一。）A和U的行空间的维数相同，都等于r。不论是A的行空间还是U行空间都是由行向量所张成的，因此，只要行向量中有多少个元素，所张成的空间就是几维。但是，如果秩r不等于方程组的行数m，也就是说消元后得到的阶梯矩阵U中存在全零行，则原矩阵A中有m-r个线性相关的行。否则，阶梯矩阵U中不存在全零行，即m=r，A中各行都线性无关。
行空间的维数：
A的行空间是由A的各行线性组合得到的，又因为每个行向量都是由n个元素组成的。因此， 他是
的一个子空间。A的行空间的维数等于阶梯矩阵U中非零行的个数，等于线性无关的行向量的个数，等于基底的个数，等于矩阵A的秩r。
举例：
首先，对这个矩阵而言，A=mxn=2x3，秩r=1。A的行空间是A的行向量的线性组合，又因为A的每行都是包含三个元素的行向量，所以，行空间是R3的子空间。
其次，A的行空间的维数等于r=1，从消元后的阶梯矩阵U中，可以发现，只有第一行对于行的线性组合有贡献。U的行空间，是用行向量[1 0 0]所张成的一条直线。是R3中的一个一维子空间。而A的行空间需要用A中的对应行向量张成。
2， A的零空间
,N for Null --- 用条件约束
如何构造零空间：
首先，对A进行高斯消元化简得到阶梯型矩阵U。观察矩阵U，看看是否存在全零行，如果有全零行，就有自由列。若存在自由列，则一定有n-r个自由列，对应有n-r个自由变量。依次让每一个自由变量为1，其余的自由变量都为0，求解Ux=0，求出n-r个特解向量x=[x1,x2,....xm]。用这n-r个特解向量作为基底，就能张成矩阵的整个零空间。（也可以看成是用n-r个自由列（特解列向量）合成0列的所有权重组合。）
Tips: A的零空间=U的零空间
零空间的维度：
对于任何mxn，即m个方程组，n个未知数的矩阵A而言，因为，零空间是矩阵A解的空间，每个解向量x都包含n个未知数，因此，他是的一个子空间。理论上说，零空间的维度=解向量的维度=未知数的个数=n，若高斯消元后的阶梯矩阵U不满秩，在U的n个列向量中，有r个主元列和n-r个自由列，n-r个自由列，对应了n-r个自由变量。则，A的零空间的维度=n-r=自由变量的个数。
A的零空间也叫A的核。
举例：
A=mxn=2x3，秩r=1。A有2个方程，3个未知数。A的零空间就是A的解的空间，任何一个解空间中的向量，都包含三个未知数，因此是R3的子空间。
A的零空间的维数等于n-r=2。因为，消元后的阶梯矩阵U有n-r=2个自由列，对应了两个自由变量。对自由变量取特殊值求解后，会得到两个特解向量。分别是列向量[0 1 0]和列向量[0 0 1]，他们可以分别张成两条相互正交的直线。A的零空间是这两条直线张成的一个二维平面，是R3中的一个二维子空间。
A的列空间与左零空间都是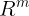
的子空间
3，A的列空间
,C for column --- 由向量张成
补充，上文中所提到的2F，即，行秩=列秩：
如何构造列空间：
A的列空间由矩阵A中的r个线性无关的列向量（即，基底）所张成的。矩阵A中的r个线性无关的列向量所在的位置，就是阶梯矩阵U中，非零主元列的位置。
列空间的维数：
A的列空间是由A的各列线性组合得到的，又因为每个列向量都包含m个元素。因此， 他是
的一个子空间。根据定理2F，阶梯矩阵U有多少个（r个）线性无关的非零行，就有多少个（r个）线性无关的非零主元列。又因为，矩阵A中线性无关的r个列向量，不仅在数量上等于，阶梯矩阵U中线性无关的列向量，并且，两个矩阵中线性无关的列向量在各自矩阵中所处的位置也相同。由此，我们得出，A的列空间的维数等于A的秩r，因为它是由r个线性无关的列向量（即，r个基底）所张成的。而这r个线性无关的列向量在A中所处的位置，等有阶梯矩阵U中r个主元列所处的位置。（注意：对于矩阵A和矩阵U而言，他们的基底所处的位置相同，但经过高斯消元后对应位置的各列向量中的元素已经发生了改变，因此，我们再次强调，A和U的列空间不同。）
关于列空间的小结：
1，A的列空间就是A的值域。
2，A的列空间和U的列空间不同，高斯消元后改变了A的列空间。
3，A和U构造基底所需的列向量所处的位置相同。阶梯矩阵U中哪几列线性无关，原矩阵A中的哪几列也线性无关。这是因为Ax=0的解和Ux=0的解相同，也就是说，A的零空间和U的零空间相同。
4，定理2F可简写为，行秩=列秩。
举例：
A=mxn=2x3，秩r=1。A的列空间是A中各列的线性组合，A中的每行都是包含两个元素的列向量，所以，是R2的子空间。
A的列空间的维数等于秩r=1。从消元后的阶梯矩阵U中，可以看到，只有第一个主元列有用，另外两个自由列对于线性组合，并没有贡献。所以，U的列空间C(U),只能是由列向量[1 0]所张成的一条过原点的直线。是R2中的一个一维子空间。而A的列空间需要用A中对应位置的列向量张成。
4，A的左零空间/
的零空间 
，N for Null --- 用条件约束
左零空间的维数：
按照零空间的定义，零空间的维数，等于解向量的维数，等于未知数的个数。回到我们之前学习的行视图与列视图，从列视图的角度看齐次方程组Ax=0，列向量x中的每一个元素（也就是未知数）就是矩阵A中每个列向量线性组合所对应的权重，而A的零空间，就是能让A的各列线性组合后得到全零列，所有可能的权重x。或者说，满足Ax=0的这一约束的全部x。mxn矩阵A共有n个列向量，每个列向量对应一个权重，共n个权重（未知数），因此，A的零空间是的子空间（从另一个角度讲，因为解向量x是一个n维向量，包含n个元素（即，未知数））。
而现在我们要求解的矩阵变成了A的转置，这样一来，零空间的求解就变成了，能够保证中各列线性组合后得到全零列的所有可能的权重x。又因为，中的列，就是A中的行，因此，我们可以认为的零空间是满足A的各行(共m行)线性组合后能够生成全零行的所有可能的权重x(即，未知数)。（这也是我自己比较满意的一种解释）
现在我们把列组合的模式x=0（这里列向量x是未知数向量），变成行组合的模式，即，用行向量
左乘A，即：
(原始矩阵A )
(如何通过列组合的方式得到全零列？注：A中的行等于A的转置中的列)
(如何通过行组合的方式得到全零行？)
x=0的零空间，是满足令A中各行的线性组合得到全零行的所有可能的权重,A共有m行，需要m个权重。因此，的零空间或者说A的左零空间的是的子空间。
同理，经过高斯消元后，可能会出现不满秩的情况，即出现了全零行，使得，非零行的个数
矩阵的行数n。那么在全部的m个列向量中，有r个主元列和m-r个自由列。m-r个自由列，对应了m-r个自由变量。则，A的左零空间的维度=m-r=自由变量的个数。
举例：
A=mxn=2x3，秩r=1。A的左零空间是A的转置矩阵的解空间，变成了3个方程，2个未知数。因此，是R2的子空间。
A的左零空间的维数等于m-r=1。A的左零空间为A的转置矩阵的零空间。转置矩阵A共有2列，根据行秩=列秩=1，则剩下一列为自由列，对应了一个自由变量，因此只能得到一个特解向量，列向量[0 1]。这一个特解向量张成了一条过零点的直线，正是A的左零空间。是R2中的一个一维子空间。
补充：
线性代数基本定理（上）
对于任意mxn矩阵A都包含4个基本子空间，线性代数基本定理的上半部分指出了每一个子空间的维度。
A:
A的零空间和行空间都是的子空间。
A的左零空间和列空间都是的子空间。
B:
1，A的列空间的维数等于秩r。
2，A的零空间的维数等于n-r。
3，A的行空间的维数等于r。
4，A的左零空间的维数等于m-r。
注意：
Rank(A)<=min(m,n)
关于维度的一些思考：
就拿矩阵A的列空间来说，假设矩阵A是一个10x8的矩阵。那么他的列空间维度本质上应该由A中任意一个列向量所包含的元素个数来决定，就拿本例来说，A的每列都有10个元素，因此，A的列空间应该是R10，即10维度。
但，根据线性代数的基本定理，A的列空间并不是完全由每列所含元素的个数决定的（本该是由元素个数决定的），而是由A的秩决定的。这就有点让人犯迷糊了，A的秩表示了，A有多少个线性无关的列，可这和每一列有多少个元素有什么关系？
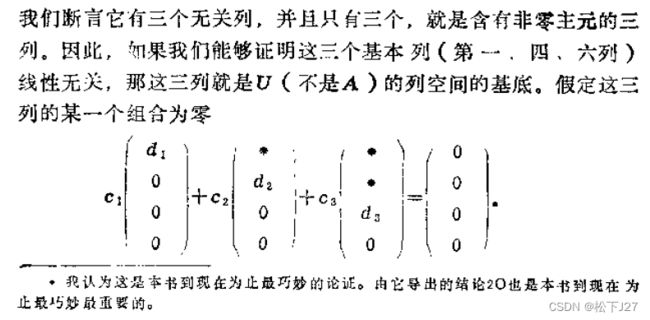
首先，我们先来看看，如果要把R10这个10维空间全部张满需要那些向量。只有一个列向量v=【1，2，3，。。。10】可以吗？不行，因为这个向量向量的线性组合只有一个形式那就是cv,最终只能得到10维空间中的一条直线。同理，只有一个列向量【1，1，1.。。。1】可以吗，也不行。只有一个列向量【1，0，0，。。。0】也不行。
虽然我们不知道矩阵A究竟是什么样的，但我们可以先试着写出可以张成10维空间的向量（基底不唯一）。看看总共究竟需要几个向量，每个向量包含几个元素。我们先从二维空间开始，要想张成一个x-y的二维平面，需要一组基底【0，1】和【1，0】，每个向量都包含两个元素。推广到三维空间，要想张成一个x-y-z三维空间，则需要【0，0，1】，【0，1，0】和【1，0，0】三个向量，且每个向量都包含三个元素。依此类推，我们要想张成一个10维空间，则需要，【1，0，。。。0】，【0，1，。。。0】一直到【0，0，。。。1】共十个向量，且这十个向量都线性无关，互相正交，同时，每个向量都包含十个元素。因此，我们知道，要想张成整个n维空间，则至少需要n个向量，且每个向量的元素个数都不能小于n，而且他们还不能线性相关，这个相关不相关的问题，就是由秩决定的。
现在我们的矩阵A是一个10x8矩阵，10行8列，每个列向量都有10个元素，但只有8列。因此，就算这8个列向量都线性无关，且正交，即秩等于8。这八个都包含10个元素的列向量，也只能张成一个8维的子空间。这就好比是把用于张成二维平面的向量【0，1】和【1，0】（在他们后各加一个0元素），拓展成【0，1，0】和【1，0，0】一样。虽然，两个向量都有三个元素且线性无关，但还是只能张成一个二维空间。对于A而言，张成R10的8个线性无关的列向量可以是：
注意，只有画红线的部分对张成8维子空间有贡献。而因为秩=8，说明对A消元后有n-r=8-8=0个自由列，共m-r=10-8=2个全零行。
（全文完）
作者 --- 松下J27
参考文献(鸣谢)：
1，线性代数及其应用，侯自新，南开大学出版社，1990.
2，Linear Algebra and Its Applications(Fourth Edition) - Gilbert Strang
格言摘抄：只要嘴巴甜，总能化到缘。(西游记动画片中猪八戒的格言)
（配图与本文无关）
版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27