【笔记】【机器学习基础】交叉验证

（一）交叉验证

交叉验证（cross-validation）是一种评估泛化性能的统计学方法，它比单次划分训练集和测试集的方法更加稳定、全面。在交叉验证中，数据被多次划分，并且需要训练多个模型。

最常用的交叉验证是 k 折交叉验证（k-fold cross-validation），其中 k 是由用户指定的数字，通常取 5 或 10。

5折交叉验证：
1、将数据划分为（大致）相等的 5 部分，每一部分叫作折（fold）
2、训练一系列模型，每折轮流作为测试集评估精度，其他作为训练集训练模型

mglearn.plots.plot_cross_validation()

得到5个精度值

通常来说，数据的前五分之一是第 1 折，第二个五分之一是第 2 折，以此类推。

一、scikit-learn中的交叉验证

scikit-learn 是利用 model_selection 模块中的 cross_val_score 函数来实现交叉验证的。cross_val_score 函数的参数是我们想要评估的模型、训练数据与真实标签。

（1）对 LogisticRegression 进行评估

from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

iris = load_iris()
logreg = LogisticRegression()

scores = cross_val_score(logreg, iris.data, iris.target)
print("Cross-validation scores: {}".format(scores))

Cross-validation scores: [0.961 0.922 0.958]

（2）修改 cv 参数来改变折数

scores = cross_val_score(logreg, iris.data, iris.target, cv=5)
print("Cross-validation scores: {}".format(scores))

Cross-validation scores: [1. 0.967 0.933 0.9 1. ]
默认情况下，cross_val_score 执行 3 折交叉验证，返回 3 个精度值。可以通过修改 cv 参数来改变折数

（3）交叉验证精度的一种常用方法（计算平均值）

print("Average cross-validation score: {:.2f}".format(scores.mean()))

Average cross-validation score: 0.96

我们可以从交叉验证平均值中得出结论，我们预计模型的平均精度约为 96%。观察 5 折交叉验证得到的所有 5 个精度值，我们还可以发现，折与折之间的精度有较大的变化，范围为从 100% 精度到 90% 精度。这可能意味着模型强烈依赖于将某个折用于训练，但也可能
只是因为数据集的数据量太小。

二、交叉验证的优点

1、train_test_split 对数据进行随机划分，可能导致测试集将仅包含“容易分类的”样例或难以分类的样例都在训练集中，但如果使用交叉验证，每个样例都会刚好在测试集中出现一次：每个样例位于一个折中，而每个折都在测试集中出现一次。因此，模型需要对数据集中所有样本的泛化能力都很好，才能让所有的交叉验证得分（及其平均值）都很高。

2、对数据进行多次划分，还可以提供我们的模型对训练集选择的敏感性信息

3、是我们对数据的使用更加高效

缺点：增加了计算成本

重要的是要记住，交叉验证不是一种构建可应用于新数据的模型的方法。交叉验证不会返回一个模型。在调用 cross_val_score 时，内部会构建多个模型，但交叉验证的目的只是评估给定算法在特定数据集上训练后的泛化性能好坏

三、分层k折交叉验证和其他策略

将数据集划分为 k 折时，从数据的前 k 分之一开始划分（正如上一节所述），这可能并不总是一个好主意。

（1）iris 数据集

from sklearn.datasets import load_iris
iris = load_iris()
print("Iris labels:\n{}".format(iris.target))

Iris labels:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]

数据的前三分之一是类别 0，中间三分之一是类别 1，最后三分之一是类别 2。 1 折将只包含类别 0，所以在数据的第一次划分中，测试集将只包含类别 0，而训练集只包含类别 1 和 2。由于在 3 次划分中训练集和测试集中的类别都不相同，因此这个数据集上的 3 折交叉验证精度为 0。

使用分层 k 折交叉验证

（1）划分数据。当数据按类别标签排序时，标准交叉验证与分层交叉验证的对比

mglearn.plots.plot_stratified_cross_validation()

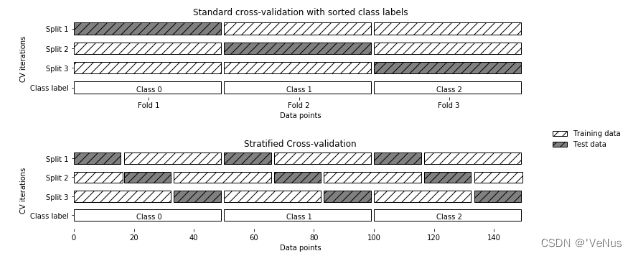
使用分层 k 折交叉验证而不是 k 折交叉验证来评估一个分类器，这通常是一个好主意，因为它可以对泛化性能做出更可靠的估计。

对于回归问题，scikit-learn 默认使用标准 k 折交叉验证。也可以尝试让每个折表示回归目标的不同取值。

1. 对交叉验证的更多控制

可以利用 cv 参数来调节 cross_val_score 所使用的折数。但 scikit-learn允许提供一个**交叉验证分离器（cross-validation splitter）**作为 cv 参数，来对数据划分过程进行更精细的控制。

回归问题默认的 k 折交叉验证与分类问题的分层 k 折交叉验证的表现都很好，但有些情况下你可能希望使用不同的策略。比如说，在一个分类数据集上使用标准 k 折交叉验证来重现别人的结果。
（1）导入 KFold 分离器类，实例化

from sklearn.model_selection import KFold
kfold = KFold(n_splits=5)

（2）以将 kfold 分离器对象作为 cv 参数传入 cross_val_score

print("Cross-validation scores:\n{}".format(
      cross_val_score(logreg, iris.data, iris.target, cv=kfold)))

可以验证，在 iris 数据集上使用 3 折交叉验证（不分层）确实是一个
非常糟糕的主意：

（3）
kfold = KFold(n_splits=3)
print(“Cross-validation scores:\n{}”.format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))

（4）
kfold = KFold(n_splits=3, shuffle=True, random_state=0)
print(“Cross-validation scores:\n{}”.format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))

2. 留一法交叉验证

from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(logreg, iris.data, iris.target, cv=loo)
print("Number of cv iterations: ", len(scores))
print("Mean accuracy: {:.2f}".format(scores.mean()))

3. 打乱划分交叉验证

mglearn.plots.plot_shuffle_split()

from sklearn.model_selection import ShuffleSplit
shuffle_split = ShuffleSplit(test_size=.5, train_size=.5, n_splits=10)
scores = cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
print("Cross-validation scores:\n{}".format(scores))

4. 分组交叉验证

mglearn.plots.plot_group_kfold()

from sklearn.model_selection import GroupKFold

X, y = make_blobs(n_samples=12, random_state=0)

groups = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
scores = cross_val_score(logreg, X, y, groups, cv=GroupKFold(n_splits=3))
print("Cross-validation scores:\n{}".format(scores))