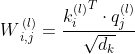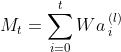论文阅读——Temporal Convolutional Attention-based Network For Sequence Modeling

https://arxiv.org/pdf/2002.12530.pdf

代码：https://github.com/haohy/TCAN

用于序列建模的基于注意力的时序卷积网络

 

作者提出一种时序卷积注意力网络 Temporal Convolutional Attention-based Netword（TCAN），包括两部分：Temporal Attention（TA）捕捉序列内部的相关特征；Enhanced Residual（ER），提取浅层的重要信息并传递到深层。

TCAN 受 Temporal Convolutional Network（TCN）的启发，利用膨胀级联网络提取输入之间的关系，并结合自注意机制提取内部信息、学习位置的依赖。TCAN由两部分组成：

TA的第 l 隐层在 t 时间步的输入是之前所有输入  的函数，保证了隐层内部不会泄露未来的信息（而自注意力则会捕捉所有时间步的信息）；

ER从TA中得到每个时间步的权重，与普通的残差相加，作为当前层的最终残差。

 

 

TCAN包含 encoder 和 decoder，encoder 和 decoder之间有L个隐层。

Encoder将长度为T的输入序列  编码为隐层(0) 的输入

使用不同膨胀率的卷积核对每个隐层进行卷积。

Decoder使用最后一个隐层的结果生成输出序列

通过四个步骤计算 t 时间步第 l+1 隐层的  

（1）使用TA得到 l 隐层的 ：  

使用三个线性函数得到  维的：keys ，queries  和 values ，计算 、（i, j = 1, 2, ..., T）：

                               

这样可以屏蔽未来时间步的权重，从而达到不使用未来信息的目的。将softmax用于  的第一个维度得到黄色块 ，每一列的权值之和可能大于1。得到可用于卷积输入的加权输出  （t = 1, 2, ..., T）：

            

（2）对 l 隐层的每个  进行膨胀卷积，得到 ；膨胀的大小随网络的深度呈指数增长， 第 l 层为

为了保持每一层的长度相同，在图(a)中每层的左侧添加了长度为  的 padding（白色的s）。这样，输入的左侧相关信息就会逐渐向右侧累积。

            

（3）在将特征图通过激活函数得到  之前，加入三个分量 , , （增强残差 ER）：

            

取  的每一行的权值之和来表示每个时间步的重要程度，得到时间步 t 的重要程度:

            

 和  的Hadamard乘积得到增强残差 。

        

 

实验结果

 

消融实验表明，TA)层比卷积层更有效，另一个是证明应用在Wl的第一维上的softmax比应用在第二维上的softmax更好。

将第一个维度上的 softmax 定义为 vertical softmax，第二个维度上的 softmax 定义为 horizontal softmax，mixed（第一个维度和第二个维度的均值）定义为 vertical+horizontal softmax。实验表明，vertical softmax 比 mixed softmax 效果好，mixed softmax 比 horizontal softmax 效果好。由于Wl是一个下三角矩阵，所以权值集中在图的左下方，第 i 行和第 j 列的权值表示第 j 个时间步对第 i 个时间步的贡献。从图4(a)可以看出，在25 - 80的时间步中，当前数据前面的3个时间步的贡献最大，除此之外，前30个左右的时间步也起到了一定的作用。相比而言，从图4(b)中可以看出，horizontal softmax 使得TA更多地集中在之前的数据上，这是不合理的，因为对于预测来说，最近的几个元素贡献最大。因此，horizontal softmax 的性能较差。对于 mixed softmax，它将过多的注意力放在第一个和最近的时间步上，而不是其他的时间步。