机器学习：线性(Fisher)判别分析

本文属于我的机器学习/深度学习系列文章，点此查看系列文章目录

前言

线性(Fisher)判别分析(Linear Discriminant Analysis, LDA)也属于线性分类方法的一种，由(Fisher,1936)提出，所以也叫Fisher判别分析。

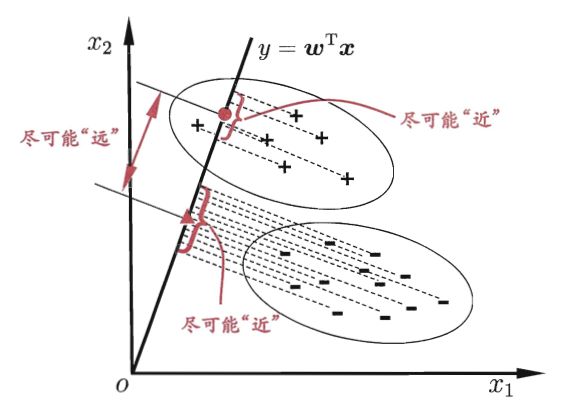
LDA的基本思想是：对于给定的训练数据样本，将样本投影到一条直线上，让同类的样例的投影点尽可能近，异类样例投影点尽可能远，这样就区分开了两类样本。当对新的样本预测时，将其投影到这条直线上，看其离哪个分类近来确定它的类别。

将上面的思想转化成对目标函数的优化，就得到了：
$$\underset{\mathbf{w}}{\max }J(\mathbf{w})=\frac{类间平均距离}{类内平均距离}$$

下图是LDA的二维示意图：

一、散度矩阵

首先设给定数据集$D=\{({\mathbf{x}}_i,y_i{)}_{i=1}^m,y_i\in \{0,1\}\}$，我们需要用给定数据去刻画类间和类内距离。

• 类间距离
  两类样本的类间距离怎么刻画？这么多点，只能通过找两个代表性的点来计算距离，显然是均值向量点。将两个均值向量(${\mu }_1,{\mu }_2$)投影到直线上，得到投影点（$m_1,m_2$）之间的距离平方$(m_1-m_2{)}^2$。 向量$\mu$在另一向量$\mathbf{w}$上的投影为${\mathbf{w}}^T\mu$(忘了的可以看机器学习：线性分类问题（基础知识）)。
  
  由此我们有
  $$\begin{gathered} 类间距离的平方=(m_1-m_2{)}^2 \\ =[{\mathbf{w}}^T({\mu }_1-{\mu }_2){]}^2 \\ =[{\mathbf{w}}^T({\mu }_1-{\mu }_2)][{\mathbf{w}}^T({\mu }_1-{\mu }_2){]}^T \\ ={\mathbf{w}}^T({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T\mathbf{w} \\ ={\mathbf{w}}^T{S}_b\mathbf{w} \\ {S}_b=({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T,类间散度矩阵 \end{gathered}$$

• 类内距离
  所谓类内距离刻画的就是同类中各个样本的松散程度，只要看每个点和均值点的距离平方和类内散裂度（类似方差）即可。类内散列度越小，意味着样本靠的越近。
  
  由此，记类内散列度为$S_c^2$有
  $$\begin{gathered} S_c^2=\sum _{i\in C}({\mathbf{w}}^T{\mathbf{x}}_i-m_c{)}^2 \\ =\sum _{i\in C}({\mathbf{w}}^T({\mathbf{x}}_i-{\mu }_c{)}^2) \\ =\sum _{i\in C}[{\mathbf{w}}^T({\mathbf{x}}_i-{\mu }_c)][{\mathbf{w}}^T({\mathbf{x}}_i-{\mu }_c){]}^T \\ =\sum _{i\in C}{\mathbf{w}}^T({\mathbf{x}}_i-{\mu }_c)({\mathbf{x}}_i-{\mu }_c{)}^T\mathbf{w} \\ ={\mathbf{w}}^T[\sum _{i\in C}({\mathbf{x}}_i-{\mu }_c)({\mathbf{x}}_i-{\mu }_c{)}^T]\mathbf{w} \end{gathered}$$
  但这只是一个分类的，要同时考虑两个分类的类内散列度，如下
  $$\begin{gathered} S_1^2+S_2^2={\mathbf{w}}^T[\sum _{i\in C_1}({\mathbf{x}}_i-{\mu }_1)({\mathbf{x}}_i-{\mu }_1{)}^T]\mathbf{w} \\ +{\mathbf{w}}^T[\sum _{i\in C_2}({\mathbf{x}}_i-{\mu }_2)({\mathbf{x}}_i-{\mu }_2{)}^T]\mathbf{w} \\ ={\mathbf{w}}^T[\sum _{j=1,2}\sum _{i\in C_j}({\mathbf{x}}_i-{\mu }_j)({\mathbf{x}}_i-{\mu }_j{)}^T]\mathbf{w} \\ ={\mathbf{w}}^T{S}_w\mathbf{w} \\ {S}_w=\sum _{j=1,2}\sum _{i\in C_j}({\mathbf{x}}_i-{\mu }_j)({\mathbf{x}}_i-{\mu }_j{)}^T,类内散度矩阵 \end{gathered}$$

  推导过程其实不难，仔细一点就能理解

二、目标函数与权重向量

有了类间距离和类内距离的刻画后， 依据上文的定义，可以得到我们的目标函数如下：
$$\begin{gathered} \underset{\mathbf{w}}{\max }J(\mathbf{w})=\frac{类间距离}{类内距离} \\ =\frac{(m_1-m_2{)}^2}{S_1^2+S_2^2} \\ =\frac{{\mathbf{w}}^T{S}_b\mathbf{w}}{{\mathbf{w}}^T{S}_w\mathbf{w}} \end{gathered}$$
理解该公式中$S_b,S_w$都是根据训练数据确定的值，我们的目标是找到使得$J$最大的$\mathbf{w}$,利用拉格朗日乘子法，原问题可转变为
$$\underset{\mathbf{w}}{\max }L(\mathbf{w},\lambda )={\mathbf{w}}^T{S}_b\mathbf{w}-\lambda ({\mathbf{w}}^T{S}_w\mathbf{w}-C)$$
对$\mathbf{w}$求偏导可得，
$$\begin{gathered} \frac{\partial L(\mathbf{w},\lambda )}{\partial \mathbf{w}}=S_b\mathbf{w}-\lambda S_w\mathbf{w}=0 \\ ⟹S_b\mathbf{w}=\lambda S_w\mathbf{w} \\ ⟹S_w^{-1}{S}_b\mathbf{w}=\lambda \mathbf{w} \end{gathered}$$
实际上到这已经发现$\mathbf{w}$是$S_w^{-1}{S}_b$的特征向量了，用求特征向量的方法即可得到$\mathbf{w}$。但是可以利用$S_b=({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T$对其进一步化简，如下
$$\begin{gathered} S_b\mathbf{w}=({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T\mathbf{w} \\ =({\mu }_1-{\mu }_2)[({\mu }_1-{\mu }_2{)}^T\mathbf{w}],[]内是个标量 \\ =\beta ({\mu }_1-{\mu }_2) \end{gathered}$$
将结果带入上面得到
$$\begin{gathered} S_w^{-1}\beta ({\mu }_1-{\mu }_2)=\lambda \mathbf{w} \\ ⟹\mathbf{w}=\frac{\beta }{\lambda }{S}_w^{-1}({\mu }_1-{\mu }_2) \\ ⟹\mathbf{w}=S_w^{-1}({\mu }_1-{\mu }_2),\frac{\beta }{\lambda }相当于对\mathbf{w}放缩，可以省略 \end{gathered}$$

至此，我们就将所需直线的方向向量$\mathbf{w}$（也是样本的权重向量）计算出来了。实际上当直线的方向确定后，各类样本在直线上投影的相对位置就确定了，即类间距离和类内距离确定。但是为了方便决策，我们希望在投影之后有一个明确的数值分解，例如0，投影结果大于0是一类，投影结果小于0是一类，而这个就是决策函数$g(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+w_0$的偏置$w_0$决定。考虑两类均值向量的中心点$\frac{1}{2}({\mu }_1+{\mu }_2)$，这个点样本讲道理应该可以任意分入两类，也可以两边都不分入，所以作为分界点最合适，我们的决策函数应该要通过该点，因此有
$$\begin{gathered} w_0=-\frac{1}{2}({\mathbf{w}}^T{\mu }_1+{\mathbf{w}}^T{\mu }_2) \\ g(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+w_0 \end{gathered}$$

三、总结

线性鉴别分析的主要思想还是很好理解的，就是一个类间距离和一个类内距离，让类间距离尽可能大，分类界限更清晰，类内距离尽可能小，同类更紧密。由上面的思想可以将Fisher鉴别分成如下几步：

1. 根据正反例求各类均值${\mu }_1,{\mu }_2$，作为类别间最大方向

2. 求类内散度矩阵$S_w$
   $$S_w=\sum _{i=1}^2\sum _{x\in C_i}(x-{\mu }_i)(x-{\mu }_i{)}^T$$

3. 求类内散度矩阵的逆$S_w^{-1}$

4. 求权重向量$\mathbf{w}$
   $$\mathbf{w}=S_w^{-1}({\mu }_1-{\mu }_2)$$

5. 计算两类投影中心$u_1,u_2$
   $$u_i={\mathbf{w}}^T{\mu }_i,i=1,2$$

6. 得到决策函数
   $$g(\mathbf{x})={\mathbf{w}}^T\mathbf{x}-\frac{1}{2}(u_1+u_2)$$

参考资料

• 周志华. 机器学习. 2016
• 周晓飞. Fisher线性鉴别推导过程