机器人中的数值优化|【一】数值优化基础
数值优化基础
凸集 Convex Sets
凸集的定义
令X是线性空间。如果对于X的子集S中的所有x和y,并且在区间 [0,1]中的所有t,点 ( 1 − t ) x + t y (1-t)x + ty (1−t)x+ty也属于S,则S称为凸集。
不失一般性,对于所有的凸集,其线性组合点都位于凸集内部:
∑ θ i x i ∈ X ∑ θ i = 1 , θ i ≥ 0 , ∀ θ i \sum \theta_{i} x_{i} \in X \\ \sum \theta_i = 1, \theta_i \geq 0, \forall \theta_i ∑θixi∈X∑θi=1,θi≥0,∀θi
凸集的性质
- 任意凸集之交为凸集。
- X的子空间为凸集。若S为凸集,则对X中任何x,x+S亦为凸集。
- 如果除了端点之外的连接x和y的线段上的每个点都在C的内部,则C是严格凸起的。
- 凸集相加为凸集
A + B = { x + y ∣ x ∈ A , y ∈ B } A+B=\{x+y \mid x \in A, y \in B\} A+B={x+y∣x∈A,y∈B} - 凸集相乘为凸集
A × B = { x × y ∣ x ∈ A , y ∈ B } A \times B=\{x \times y \mid x \in A, y \in B\} A×B={x×y∣x∈A,y∈B} - 凸集相交不为凸集
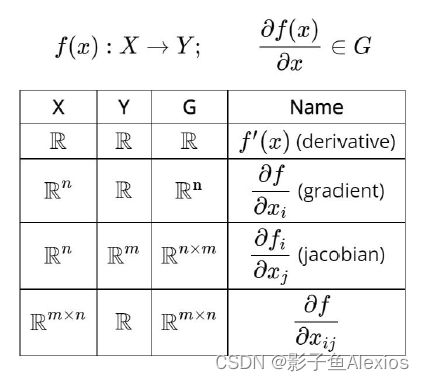
High-Order Info of Functions
Functions f ( x ) = f ( x 1 , x 2 , x 3 ) f(x)=f\left(x_1, x_2, x_3\right) f(x)=f(x1,x2,x3)
Gradient ∇ f ( x ) = ( ∂ 1 f ( x ) ∂ 2 f ( x ) ∂ 3 f ( x ) ) \nabla f(x)=\left(\begin{array}{l}\partial_1 f(x) \\ \partial_2 f(x) \\ \partial_3 f(x)\end{array}\right) ∇f(x)= ∂1f(x)∂2f(x)∂3f(x)
Hessian ∇ 2 f ( x ) = ( ∂ 1 2 f ( x ) ∂ 1 ∂ 2 f ( x ) ∂ 1 ∂ 3 f ( x ) ∂ 2 ∂ 1 f ( x ) ∂ 2 2 f ( x ) ∂ 2 ∂ 3 f ( x ) ∂ 3 ∂ 1 f ( x ) ∂ 3 ∂ 2 f ( x ) ∂ 3 2 f ( x ) ) \nabla^2 f(x)=\left(\begin{array}{ccc}\partial_1^2 f(x) & \partial_1 \partial_2 f(x) & \partial_1 \partial_3 f(x) \\ \partial_2 \partial_1 f(x) & \partial_2^2 f(x) & \partial_2 \partial_3 f(x) \\ \partial_3 \partial_1 f(x) & \partial_3 \partial_2 f(x) & \partial_3^2 f(x)\end{array}\right) ∇2f(x)= ∂12f(x)∂2∂1f(x)∂3∂1f(x)∂1∂2f(x)∂22f(x)∂3∂2f(x)∂1∂3f(x)∂2∂3f(x)∂32f(x)
在0点处的近似:泰勒展开
f ( x ) = f ( 0 ) + x T ∇ f ( 0 ) + 1 2 x T ∇ 2 f ( 0 ) x + O ( ∥ x − x 0 ∥ 3 ) \quad f(x)=f(0)+x^T \nabla f(0)+\frac{1}{2} x^T \nabla^2 f(0) x+O\left(\left\|x-x_0\right\|^3\right) f(x)=f(0)+xT∇f(0)+21xT∇2f(0)x+O(∥x−x0∥3)
现在拓展概念,设将 f ( x ) f(x) f(x)为维度从n维到m维的映射,即 f ( x ) : R n → R m f(x): \mathbb{R}^n \rightarrow \mathbb{R}^m f(x):Rn→Rm,则有Jacobian矩阵
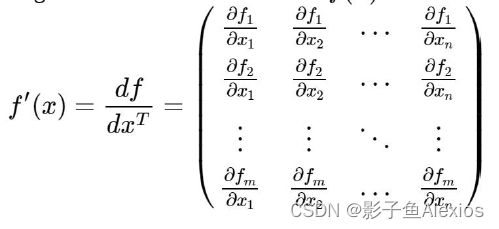
矩阵和向量微分规则与表格
一些有用的性质
d A = 0 d ( α X ) = α ( d X ) d ( A X B ) = A ( d X ) B d ( X + Y ) = d X + d Y d ( X T ) = ( d X ) T d ( X Y ) = ( d X ) Y + X ( d Y ) d < X , Y > = < d X , Y > + < X , d Y > d ( X ϕ ) = ϕ d X − ( d ϕ ) X ϕ 2 d t r X = I d f ( g ( x ) ) = f g d ˙ g ( x ) dA = 0\\ d(\alpha X) = \alpha (dX)\\ d(AXB) = A(dX)B\\ d(X+Y) = dX + dY\\ d(X^T) = (dX)^T\\ d(XY) = (dX)Y + X(dY)\\ d
规则可以参考wikipedia网站MATRIX CALCULUS
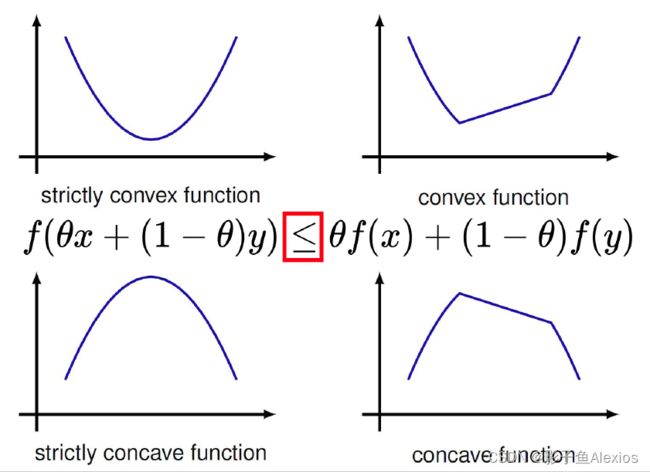
凸函数的性质 Convex Functions
Jensen不等式
凸函数满足Jensen不等式,如下所示
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)


一阶条件 First-order conditions
f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) f(y) \geq f(x)+\nabla f(x)^T(y-x) f(y)≥f(x)+∇f(x)T(y−x)
当 ∇ f ( x ) T = 0 \nabla f(x)^T=0 ∇f(x)T=0时,有 f ( y ) ≥ f ( x ) f(y) \geq f(x) f(y)≥f(x)
二阶条件 Second-order conditions
一个光滑函数为凸函数,当且仅当
∇ 2 f ( x ) ⪰ 0 , ∀ x \nabla^2 f(x) \succeq 0, \forall x ∇2f(x)⪰0,∀x
即函数的二阶导数半正定
对于非凸函数,局部最小值满足
∇ 2 f ( x ∗ ) ⪰ 0 , \nabla^2 f(x^*) \succeq 0, ∇2f(x∗)⪰0,
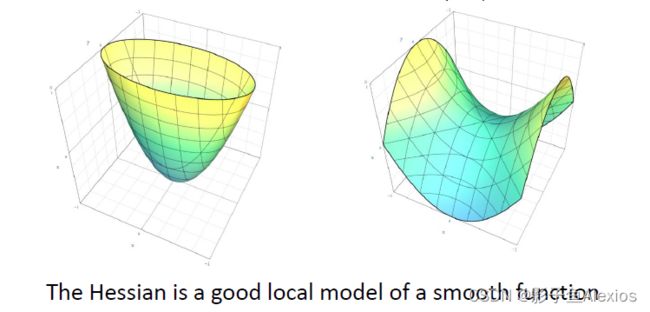
强凸性 strong convexity
f ( y ) ≥ f ( x ) + ( y − x ) T ∇ f ( x ) + m 2 ∥ y − x ∥ 2 f(y) \geq f(x)+(y-x)^T \nabla f(x)+\frac{m}{2}\|y-x\|^2 f(y)≥f(x)+(y−x)T∇f(x)+2m∥y−x∥2
式中前两部分对所有凸函数适用,第三部分也就是最后一部分为min curvature
当 f ( x ) f(x) f(x)有Hessian阵时,有
f ( y ) ≈ f ( x ) + ( y − x ) T ∇ f ( x ) + 1 2 ( y − x ) T ∇ 2 f ( x ) ( y − x ) ≥ f ( x ) + ( y − x ) T ∇ f ( x ) + λ min 2 ∥ y − x ∥ 2 \begin{aligned} f(y) & \approx f(x)+(y-x)^T \nabla f(x)+\frac{1}{2}(y-x)^T \nabla^2 f(x)(y-x) \\ & \geq f(x)+(y-x)^T \nabla f(x)+\frac{\lambda_{\min }}{2}\|y-x\|^2 \end{aligned} f(y)≈f(x)+(y−x)T∇f(x)+21(y−x)T∇2f(x)(y−x)≥f(x)+(y−x)T∇f(x)+2λmin∥y−x∥2
则有
∇ 2 f ( x ) ⪰ m I \nabla^2 f(x) \succeq m I ∇2f(x)⪰mI
Lipchitz常数
Lipchitz常数满足
∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ M ∥ y − x ∥ \|\nabla f(x)-\nabla f(y)\| \leq M\|y-x\| ∥∇f(x)−∇f(y)∥≤M∥y−x∥
由近似展开可以得到
f ( y ) ≤ f ( x ) + ( y − x ) T ∇ f ( x ) + M 2 ∥ y − x ∥ 2 f(y) \leq f(x)+(y-x)^T \nabla f(x)+\frac{M}{2}\|y-x\|^2 f(y)≤f(x)+(y−x)T∇f(x)+2M∥y−x∥2
有
f ( y ) − f ( x ⋆ ) ≥ m 2 ∥ y − x ⋆ ∥ 2 f(y)-f\left(x^{\star}\right) \geq \frac{m}{2}\left\|y-x^{\star}\right\|^2 f(y)−f(x⋆)≥2m∥y−x⋆∥2
f ( y ) − f ( x ⋆ ) ≤ M 2 ∥ y − x ⋆ ∥ 2 f(y)-f\left(x^{\star}\right) \leq \frac{M}{2}\left\|y-x^{\star}\right\|^2 f(y)−f(x⋆)≤2M∥y−x⋆∥2
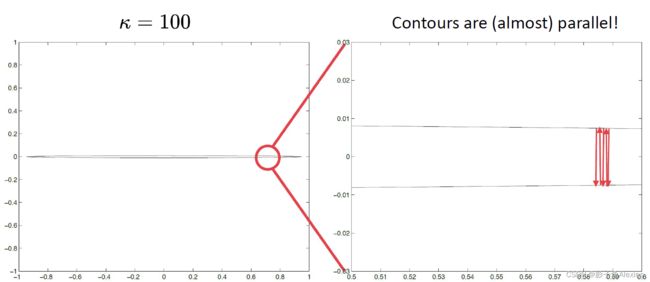
条件数 condition number
对于任何函数,有 κ = m a j o r a x i s m i n o r a x i s \kappa=\frac{major \quad axis}{minor \quad axis} κ=minoraxismajoraxis
对于光滑函数,有 κ ≈ c o n d ( ∇ 2 f ( x ) ) \kappa \approx cond(\nabla^2f(x)) κ≈cond(∇2f(x))
对于可微函数,有 κ = M / m \kappa = M/m κ=M/m
Sub-differential
对于不光滑的函数,其导数在一点左右不相等,我们称之为sub differential

记为 ∂ f ( x ) = { g : f ( y ) > f ( x ) + ( y − x ) T g , ∀ y } \partial f(x)=\left\{g: f(y)>f(x)+(y-x)^T g, \forall y\right\} ∂f(x)={g:f(y)>f(x)+(y−x)Tg,∀y}

sub-differential的方向不唯一,但是最速下降的方向是负sub-diff中模长最小的方向
单调性Monotonicity
无约束非凸函数优化
min f ( x ) x = ( x 1 , . . . , x n ) ∈ R n : o p t i m i z a t i o n v a r i a b l e s f : R n → R : o b j e c t i v e f u n c t i o n \min f(x)\\ x = (x_1,...,x_n) \in \mathbb{R}^n : optimization variables\\ f:\mathbb{R}^n \rightarrow \mathbb{R} : objective function minf(x)x=(x1,...,xn)∈Rn:optimizationvariablesf:Rn→R:objectivefunction
线性搜索最速梯度下降 Line-Search Steepest Gradient Descent
最速梯度下降的迭代形式如下所示
x k + 1 = x k − τ ∇ f ( x k ) x^{k+1}=x^k-\tau \nabla f\left(x^k\right) xk+1=xk−τ∇f(xk)
其中 τ \tau τ为步长。
选择步长的方法有多种,如下所示
- 1.常数 constant step size
τ = c \tau = c τ=c - 2.随着时间减小 diminishing step size
τ = c / k \tau = c/k τ=c/k - 3.精确线性搜索 exact line search
τ = arg min α f ( x k + α d ) \tau = \arg \min_{\alpha} f(x^k + \alpha d) τ=argαminf(xk+αd) - 4.非精确线性搜索 inexact line search
τ ∈ { α ∣ f ( x k ) − f ( x k + α d ) ≥ − c ⋅ α d T ∇ f ( x k ) } \tau \in\left\{\alpha \mid f\left(x^k\right)-f\left(x^k+\alpha d\right) \geq-c \cdot \alpha d^{\mathrm{T}} \nabla f\left(x^k\right)\right\} τ∈{α∣f(xk)−f(xk+αd)≥−c⋅αdT∇f(xk)}
其中方法1过于代办,方法2需要满足robbins-monro规则,对于一些很复杂计算很昂贵的函数来说是适合用的,方法3不具备可行性,方法4需要满足Armijo条件,较为容易满足。
Backtracking/Armijo line search
- 选择搜索方向: d = − ∇ f ( x k ) d=-\nabla f\left(x^k\right) d=−∇f(xk)
- 当 f ( x k + τ d ) > f ( x k ) + c ⋅ τ d T ∇ f ( x k ) f\left(x^k+\tau d\right)>f\left(x^k\right)+c \cdot \tau d^T \nabla f\left(x^k\right) f(xk+τd)>f(xk)+c⋅τdT∇f(xk)时,重复 τ ← τ / 2 \tau \leftarrow \tau/2 τ←τ/2
- 迭代 x k + 1 = x k + τ d x^{k+1}=x^k+\tau d xk+1=xk+τd
重复直至梯度很小或者sub-diff包含0时。
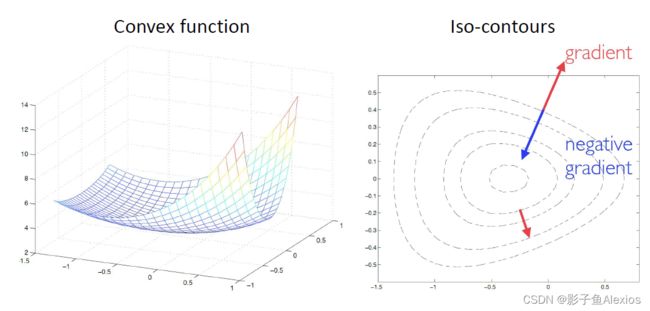
Backtracking的缺点
当条件数很大,或者函数很差的时候,可能会反复震荡。如下图所示,当我们在优化一个非常扁的椭圆形函数的时候,就会出现这样在椭圆上往复震荡的情况,因此我们发现,很有必要了解到函数的曲率,将其纳入考虑范围。
改进牛顿法 Modified Damped Newton’s Method
牛顿法
根据泰勒二阶展开,有
f ( x ) ≈ f ^ ( x ) = f ( x k ) + ∇ f ( x k ) T ( x − x k ) + 1 2 ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) f(x) \approx \hat{f}(x) = f(x_k) + \nabla f(x_k)^T(x - x_k) + \frac{1}{2}(x-x_k)^T \nabla^2 f(x_k)(x-x_k) f(x)≈f^(x)=f(xk)+∇f(xk)T(x−xk)+21(x−xk)T∇2f(xk)(x−xk)
最小化二阶近似
∇ f ^ ( x ) = ∇ 2 f ( x k ) ( x − x k ) + ∇ f ( x k ) = 0 \nabla \hat{f}(x) = \nabla^2 f(x_k)(x - x_k) + \nabla f(x_k) = 0 ∇f^(x)=∇2f(xk)(x−xk)+∇f(xk)=0
得到给定 ∇ 2 f ( x k ) ≻ 0 \nabla^2 f(x_k) \succ 0 ∇2f(xk)≻0时,有
x = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) x = x_k - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k) x=xk−[∇2f(xk)]−1∇f(xk)
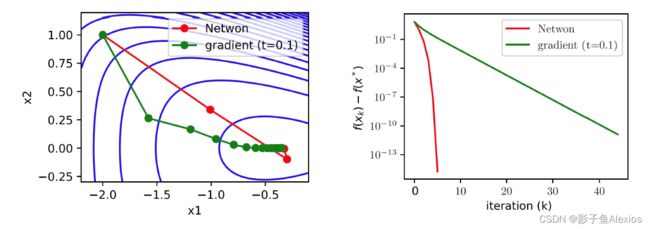
牛顿步骤为
x k + 1 = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) x_{k+1} = x_k - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k) xk+1=xk−[∇2f(xk)]−1∇f(xk)
其优化过程如下图所示
牛顿法缺点
Hessian阵可能是奇异的,且不稳定的,这样的话我们无法对Hessian阵进行求逆运算。
可行牛顿法
首先初始化 x x x, x ← x 0 ∈ R n x \leftarrow x_0 \in \mathbb{R}^n x←x0∈Rn
当 ∣ ∣ ∇ f ( x ) ∣ ∣ > δ ||\nabla f(x)|| > \delta ∣∣∇f(x)∣∣>δ时,进行如下计算
d o do do:
d ← − M − 1 ∇ f ( x ) d \leftarrow -M^{-1} \nabla f(x) d←−M−1∇f(x)
t ← b a c k t r a c k i o n g l i n e s e a r c h t \leftarrow backtrackiong \quad line \quad search t←backtrackionglinesearch
x ← x + t d x \leftarrow x + td x←x+td
e n d w h i l e end \quad while endwhile
r e t u r n return return
其中,M是一个接近Hessian阵的正定矩阵,以此来替代线性搜索中的求梯度和求Hessian阵。
如果函数为凸函数,则有
M = ∇ 2 f ( x ) + ϵ I , ϵ = min ( 1 , ∥ ∇ f ( x ) ∥ ∞ ) / 10 \boldsymbol{M}=\nabla^2 f(\boldsymbol{x})+\epsilon \boldsymbol{I}, \epsilon=\min \left(1,\|\nabla f(\boldsymbol{x})\|_{\infty}\right) / 10 M=∇2f(x)+ϵI,ϵ=min(1,∥∇f(x)∥∞)/10
因为M是正定的,因此可以使用Cholesky factorization
M d = − ∇ f ( x ) , M = L L T \boldsymbol{M} \boldsymbol{d}=-\nabla f(\boldsymbol{x}), \boldsymbol{M}=\boldsymbol{L} \boldsymbol{L}^{\mathrm{T}} Md=−∇f(x),M=LLT
如果函数是非凸的,那么我们通过如下计算M
Bunch-Kaufman Factorization:
M d = − ∇ f ( x ) , M = L B L T \boldsymbol{M} \boldsymbol{d}=-\nabla f(\boldsymbol{x}), \boldsymbol{M}=\boldsymbol{L} \boldsymbol{B} \boldsymbol{L}^{\mathrm{T}} Md=−∇f(x),M=LBLT