论文阅读：（arXiv 2021）COIN:COmpression with Implicit Neural Representaions

COIN:COmpression with Implicit Neural Representaions (arXiv 2021)

Paper:https://arxiv.org/abs/2103.03123
Code:https://github.com/EmilienDupont/coin

2022/6/10:这篇文章其实早就看完了，而且看过两三遍了吧应该。随便写写当做今天的工作任务好了，晚上有朋友约了打游戏滴滴滴。

2022/6/11:现在动身回去休息，早上起来写一个COIN代码的讲解或者说注释吧，虽然没有粉丝，但是大家如果有想看或推荐的论文可以评论或私信告诉我。嘻嘻嘻嘻·····

Abstract

提出了一种图像压缩的新方法，不是将一副图像每个像素的RGB值保存起来，而是保存过拟合图像的神经网络的权重。具体来说，为了编码一个图像，我们使用了一个MLP用于将像素位置映射到RGB值。之后量化并储存这个MLP的权重作为这个图像的编码。要解码图像时，简单在每个像素点处评估该MLP即可。我们发现这种简单的方法可以在低码率处优于JPEG，甚至不需要任何的熵编码和学习权重分布。虽然现在我们的方法还不能与最先进的压缩方法竞争，我们表明它有各种吸引人的性质，可以使它成为一中可行的替代其他神经数据压缩方法。

1. Introduction

神经图像压缩方法通常在自动编码器设置中运行,发送方使用编码器将输入数据映射到离散的潜在码，然后根据习得的潜在分布将其熵编码到位流中。比特流被传输到接收端，接收端将其解码为潜在码，最终通过解码器重建图像。

在本文中，我们采用了一种不同的方法:我们用一个小的MLP对图像进行过拟合，将像素位置映射到RGB值，然后将这个MLP的权值θ作为图像的编码(见图1)。然而，由于自然图像中包含的高频信息，过拟合这种MLPs(即隐式神经表示)是困难的。最近的研究表明，这种情况可以通过使用正弦编码和激活来缓解。在这项工作中，我们展示了使用带有正弦激活的MLPs(通常称为SIRENs[30])，我们可以用小得惊人的网络(8k参数)来匹配大图像(393k像素)。

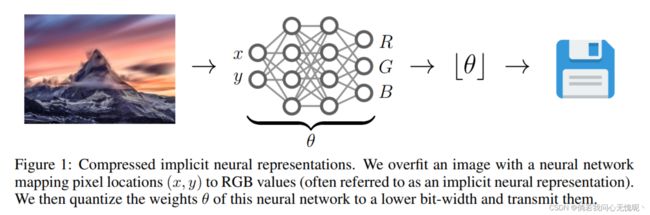
我们在标准图像压缩任务上评估了我们的方法，并表明我们在低比特率下优于JPEG，即使没有熵编码或学习权重分布。由于隐式表示已经成功地应用在生成建模[10]的背景下，很可能将我们的方法与学习的权重分布相结合，可能会导致有前途的神经数据压缩新方法。进一步，通过将我们的图像作为一个从像素位置到RGB值的函数。我们可以简单地通过在逐步提高的分辨率上评估函数来执行渐进式解码，这对资源受限的终端设备特别有吸引力。

2. Method

在本节中，我们描述了压缩隐式神经表示(COIN)，我们提出的图像压缩方法。编码步骤包括将MLP过拟合到图像上，量化其权重并传输这些权重。在解码时，在所有像素位置评估传输的MLP，以重建图像。

2.1 Encoding

令$I$为我们希望编码的图像，那么$I[x,y]$代表在像素位置$[x,y]$处的RGB值。我们定一个包含参数$\theta$的函数$f_{\theta }(x,y)=(r,g,b)$，其从图像像素位置映射到RGB值处。我们可以通过使$f_{\theta }$在某些失真测度下过拟合来编码这张图像。在本文中，我们使用MSE损失，则可以表示为以下优化问题。
选择$f_{\theta }$的参数化方式是至关重要的。事实上，用标准激活函数的MLP参数化$f_{\theta }$会导致欠拟合，即使使用大量参数。这个问题可以用多种方法来解决，例如用傅里叶特征[34]编码像素坐标，或者使用正弦激活函数[30]。根据经验，我们发现对于给定的参数预算，后一种选择产生了更好的结果。对于一个足够大的MLP，最小化方程(1)是微不足道的。但是，我们将MLP的参数θ存储为图像的压缩描述，因此限制权值的数量可以提高压缩率。因此，目标是拟合fθ到I(即，最小化失真)使用尽可能少的参数(即，最大化的速率)。然后，我们的方法有效地将数据压缩问题转换为模型压缩问题。

为了减小模型的大小，我们考虑两种方法:体系结构搜索和权重量化。更具体地说，我们对层的宽度和层数执行超参数扫描MLP，并将权值的精度从32位量化到16位，这足以在低比特率的情况下超过JPEG标准。然而，我们相信更复杂的架构搜索[11]的方法，特别是模型压缩[36,13,37]将进一步提高结果。

2.2 Decoding

给定存储的量化权重$\theta$，解码只需计算每个像素位置的函数$f_{\theta }$来重建图像。这种解码方式给了我们额外的灵活性:我们可以逐步解码图像，例如，先解码部分影像或者低分辨率影像，这只需要简单的解码部分像素位置函数即可。 以这种方式部分解码图像对于基于自动编码器的方法是困难的，这显示了COIN方法的进一步优势。

3. Related Work

隐式神经表示： 用神经网络表示数据最初是由[32]提出的，但最近在3D视觉社区的兴趣激增。因为深度体素表示的内存需求呈立方体增长，提出隐式表示方法对高分辨率信号进行压缩编码。而用于表示图像的mlp通常只有相对较少的参数我，们更进一步，通过仔细选择MLP的架构和量化权重，与存储RGB值相比，我们可以使用占用的空间明显更少的MLPs来匹配图像。

神经数据压缩： 学习图像压缩方法通常基于分层变分自编码器，通过对先验和潜变量进行离散化以实现熵编码。在类似的脉络工作的潜变量模型文献，几项研究[5,12,39]试图通过在平摊推理网络的基础上，采用基于梯度的迭代优化步骤来缩小摊销缺口[8]。[39]还通过推断每个实例的优化时间来识别并试图缩小潜在变量量化所导致的离散化差距。[38]进一步采用了模型的实例级优化的思想:它们对解码器进行实例级微调，并随潜在码一起传输量化的解码器参数更新，从而提高了率失真性能。在本文中，我们采用了一种不同的、甚至更极端的、从每个实例优化的角度出发的方法:我们优化MLP来过拟合单个图像，并将其权重作为图像的压缩描述传递。

模型压缩： 虽然众所周知，数据和模型压缩的问题是非常密切相关的，但COIN明确地将数据压缩问题转换为模型压缩问题。关于模型压缩的文献非常丰富，[36,21,13,37,18,15]，可以用来提高COIN的性能。

4. Experiments

我们在柯达图像数据集[17]上进行实验，该数据集包含24张大小为768×512的图像。我们将我们的模型与三种基于自编码器的神经压缩基线进行比较，我们称之为BMS[2]、MBT[24]和CST[7]。我们还与JPEG、JPEG2000、bgp和VTM图像编解码器进行了比较。为了对我们的模型进行基准测试，我们使用了CompressAI库[4]和其中提供的预训练模型。我们在PyTorch[28]中实现我们的模型，并在单个RTX2080Ti GPU上执行所有实验。

率失真作图： 确定给定参数预算的最佳模型架构(以比特每像素或bpp计算)，我们首先找到深度和宽度的有效组合表示图像的MLP。例如，对于使用16位权值的0.3bpp，有效的网络包括
MLPs有10层宽28层，7层宽34层等等。然后，我们通过在单一图像上使用贝叶斯优化运行学习率和有效架构的超参数搜索来选择最佳架构(我们发现建筑搜索的结果很好地运用到了其他图片上)。生成的模型对数据集中的每幅图像进行32位精度的训练，训练后转换为16位精度。我们注意到降低权重的精度32位到16位训练后导致失真几乎没有增加，但是将它们进一步降低到8位会产生大量的失真，这超过了将bpp减半的好处。

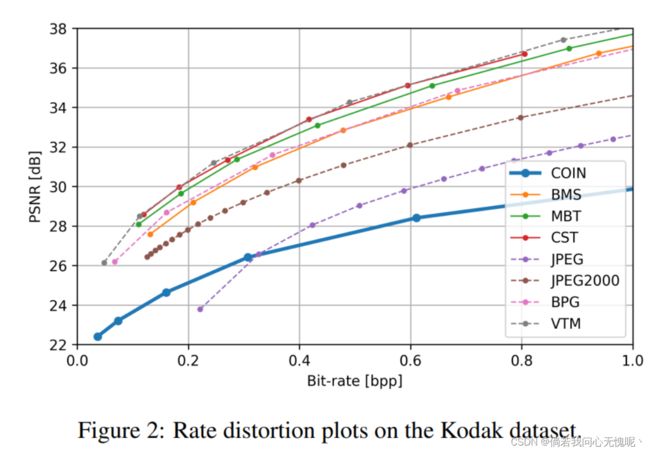
图2显示了该过程在不同bpp级别上的结果。可以看到，在低比特率下，即使不使用熵编码，我们的模型也比JPEG有所改进。虽然我们的方法还远远没有达到最先进的压缩方法的水平，但我们相信，这种简单方法的性能对未来在这个方向上的工作是有希望的。

模型大小： 与大多数其他神经数据压缩算法相比，我们的方法在测试时不需要解码器。事实上，虽然在基于编解码器方法中表示压缩图像的隐式编码很小，但解码器模型很大(通常比未压缩的图像大得多)。因此，解码设备上所需的内存也很大。在我们的例子中，我们只需要一个(非常小的)MLP在解码器端的权重，导致内存需求减少了几个数量级。如图3所示，在0.3bpp时，我们的方法需要14kB，而其他基线需要10MB到40MB。

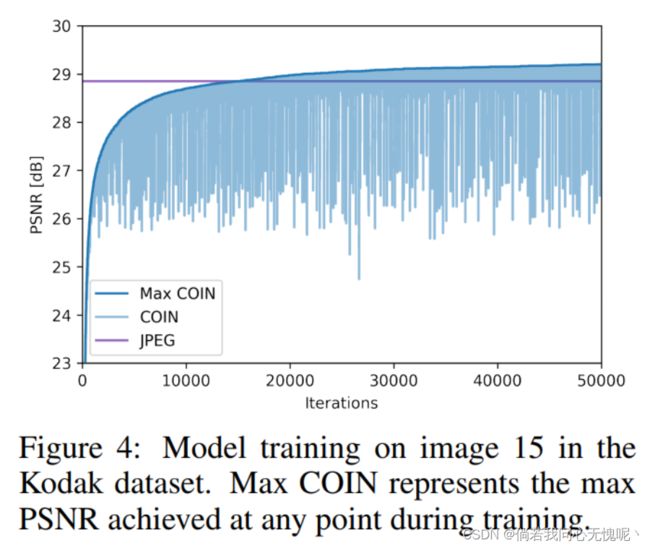
编码动态优化： 图4展示了过拟合过程的一个示例。可以看出，COIN在15k次迭代后优于JPEG，并且在此基础上继续改进。优化过程会有噪声，我们只简单的保存了PSNR最好的模型。

架构选择： 在图5中，我们展示了各种有效的0.3 bpp规模架构的性能。可以看出，压缩的质量取决于架构的选择，不同的bpp值有不同的最佳架构，详见附录A。

5. Score, Limitations and Future Work

局限性： 我们的方法的主要限制是编码速度慢，因为我们必须为每个编码的图像解决一个优化问题。然而，预先支付大量的计算成本来压缩内容，以便传递给许多接收者，这是一对多媒体分发设置的标准做法，例如Netflix[1]。然而，使用元学习[29,33]或平摊推理[35,40]方法可能会避开这一限制。此外，在解码时，我们需要评估每个像素位置的网络，以解码完整的图像。然而，这种计算可能会被并行化到对所有像素进行一次向前传递的地步。最后，我们的方法比目前最先进的压缩方法性能更差。然而，我们相信有几个有希望的方向来缩小这一差距。

未来的工作： 隐式表示[10]的生成建模最近的工作表明，学习函数权重的分布可以转化为我们的方法的显著压缩收益。此外，探索元学习或其他摊销方法以加快编码速度可能是未来工作的一个重要方向[29,33]。细化表示图像的函数架构(例如通过神经架构搜索或修剪)是另一个有前途的途径。虽然在本文中我们只是简单地将权重转换为半精度，但使用更高级的模型压缩可能会在性能上获得很大的提高。最后，由于隐式表示将任意坐标映射到任意特征[34,30,10]，因此将我们的方法应用于不同类型的数据(如视频或音频)会很有趣。

6. Conclusion

在本文中，我们提出了一种新的图像压缩方法，通过将神经网络拟合到像素，并存储得到的模型的权值。我们通过实验表明，即使不使用熵编码，这种简单的方法也可以在低比特率下优于JPEG。我们希望在这一领域的进一步工作将导致神经数据压缩的一类新方法。

A. Experimental Details

所有模型都使用Adam进行了50k次的训练。我们使用两个输入维度的mlp(对应于$(x,y)$坐标)和3个输出维度(对应RGB值)。坐标被归一化为$[-1,1]$， RGB值归一化到$[0,1]$。除了最后一层，我们在每一层都使用正弦非线性，并使用中描述的初始化。我们使用的学习率是$2\times 10^{-4}$。下面我们将描述每个bpp级别的架构。

再现论文中所有实验的代码可以在https://github.com/EmilienDupont/coin找到。

B. Additional Results

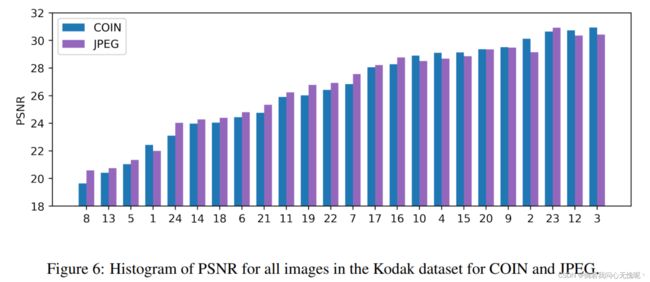
在图6中，我们绘制了柯达数据集中所有图像在0.3bpp时COIN和JPEG的性能(因为COIN和JPEG在这个比特率下的性能类似)。可以看出，失真值是紧密相连的，COIN难以编码的图像，JPEG也难以编码。

C. Qualitative Results

在此基础上，在柯达数据集上，对COIN和JPEG压缩结果进行定性比较。