深度学习的求导实现‍

深度学习的求导实现‍

介绍神经网络的训练过程

这里就是介绍一种方式，梯度下降，但神经网络的优化可不仅只有梯度下降可以优化，只是梯度下降已经成为主流。可以参考一下包括但不限于：

动量下降，Adam(学习率自适应算法)一般用于优化器,RMSProp()，牛顿法，共轭梯度等

回归正题，神经网络怎么训练的呢。大体可分为4个步骤

1.数据的预处理

对设计的模型所需数据进行一定的处理，比如正则化，标准化，数据集增强（这里也可以放进网络），噪声鲁棒性。将所有的数据处理成模型所需的数据集。

2.模型的搭建

根据所处理的问题，所要完成的业务进行网络模型搭建，包括基本前馈神经网络，卷积型网络，序列型网络等。具体构建根据效果和模型分析进行选择。

这里一般不会所有机器学习中的除神经网络的算法

3.前向推理（传播）

所谓的前向传播就是将输入的数据在经过神经网络计算得到网络计算的值，也就是预测值

4.反向传播，梯度更新

反向传播的前提一般是可导的，但面对不可导的时候还是会有一些处理方法，包括有次梯度和重参数化等。简单的说，前向传播参数是固定的，所以自变量是数据本身，而反向传播，因为计算节点是固定的，所以计算的函数就固定了，那么可以根据损失函数和网络的参数建立一个坐标系，在以网络参数为变量，对损失函数求导，这样就可以有一个梯度，有这个梯度还是不够的，因为我们的网络参数还是没有改变，这时候就需要更新参数了，这里面就涉及一个重要的法则了：链式法则。至此，反向传播也就结束了。

给出一个案例

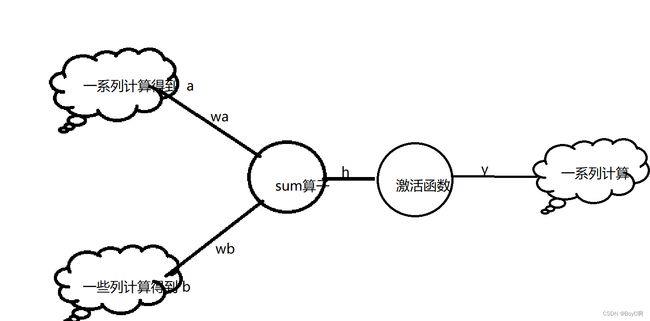
就上述例子而言，在输入值通过前面的网络到达这个sum节点的时候，前向传播就可以写为

h = a * wa + b * wb + 0这里的0在上述途中并未画出，代表的是sum算子的偏置

y = 激活函数（h）

然后进行下一步计算，这就是前向传播中的一小部分，展开全局就会看到全部的前向传播，这里就不展开了。对上述进行简化得到计算图：

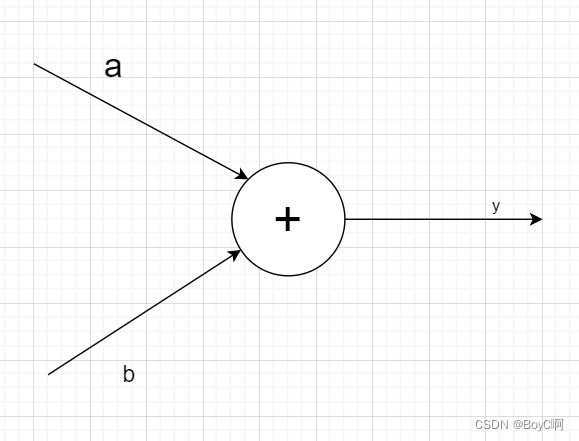
这可以看作一个神经元，前面后面还有计算，这样比较好理解后面的玩意。这里要提醒一下，损失函数还没有出现，只有前向传播结束后得到一个标量，通过这个标量才可以计算损失，回到这个计算图。

y = a + b

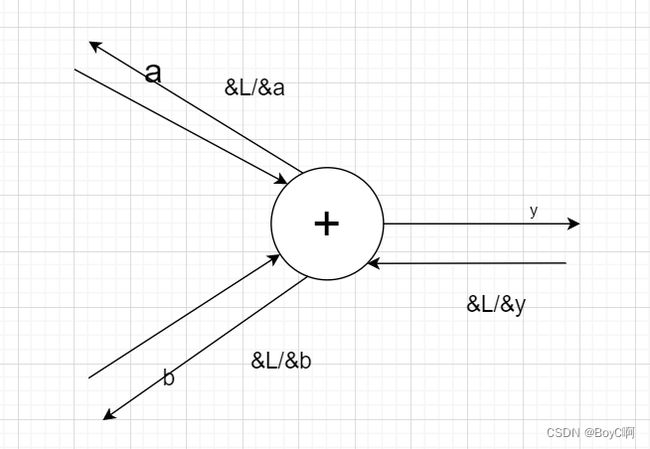
我们的目标是反向传播，

这应该是大致的反向传播。此时，传播的值是指最终的输出 L 关于各个变量的导数。在这个 例子中，关于 y的导数是 ∂L /∂y，关于 x 和 y 的导数分别是 ∂L/ ∂a 和 ∂L /∂b。

链式法则是复合函数的求导法 则，其中复合函数是由多个函数构成的函数。

这里考虑 y = f(x) 和 z = g(y) 这两个函 数。如 z = g(f(x)) 所示，最终的输出 z 由两个函数计算而来。此时，z 关 于 x 的导数可以按下式求得： ∂z /∂x = ∂z/ ∂y * ∂y /∂x

z 关于 x 的导数由 y = f(x) 的导数和 z = g(y) 的导 数之积求得，这就是链式法则。

按照这个法则：

因此，在上面的例子中， ∂L/ ∂a = ∂L /∂y *∂y /∂a ， ∂L /∂b = ∂L /∂y *∂y /∂b

在按照上述的计算图所示，∂y /∂a 和∂y /∂b 都为1

所以a处反向传出的还是∂L /∂y* 1，b处反向传出的还是∂L /∂y *1

现在，请记住加法节点的反向传播的传出是什么。没错，他不会改变之前反向传过来的梯度，只是简单的分发出去

同理乘法节点也可以算到 没错就是交换a 和 b

所以a处反向传出的还是∂L /∂y* b，b处反向传出的还是∂L /∂y *a

现在请你把∂L /∂y* b看作∂L /∂y

然后再a处反向传播后继续画出一个计算图，然后就可以理解全程的反向传播了，而我们要计算的就是每个节点的分别求导了。反正我感觉很清晰。

这也就是一个超级超级多的复合函数求导吗，而且都是有计算图公式的计算，对计算机来说简直不要太简单。

深度学习求导：

基于上述补充，在深度学习里面，节点总是出乎意料，又在意料之中的，这里继续介绍关于分支节点的反向传播：

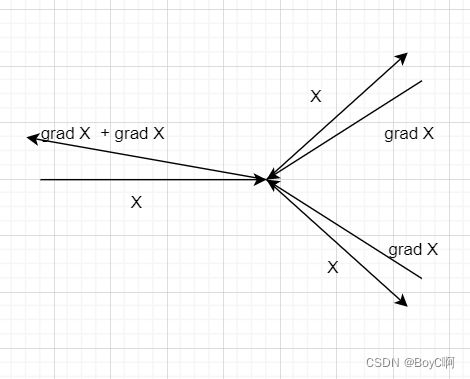
计算图:

简单明了 ，分支节点的反向传播就是相加在返回，其实就是一个相同的值复制给两个神经元。

还有包括Repeat节点 ，多数和的Sum节点，图不好画，想了解的小伙伴可以自行了解。

现在上正题了。矩阵中的反向传播。

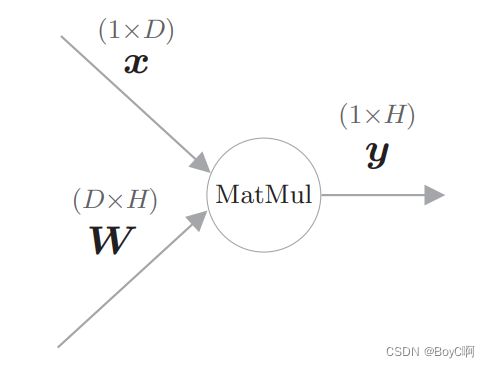
为了解释 矩阵乘节点，我们来考虑 y = XW 这个计算。这里，X、 W、y 的形状分别是 1 × D、D × H、1 × H

计算图：

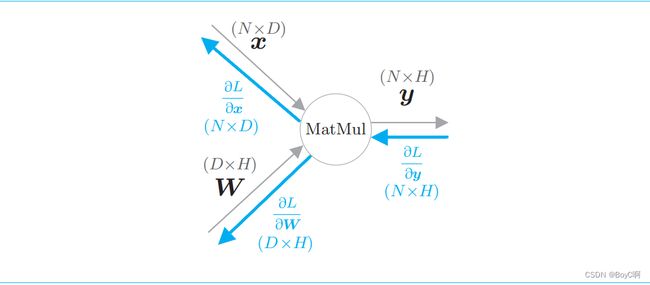
这里直接保留原文的解释。

这里就是一个多元微分的基本知识，那么记住就ok,梯度是如何计算的。

grad X = grad Y @ W^T @ 表示矩阵乘，^T表示转置

grad W = X^T @ grad Y

详细推导请参考神经网络反向传播的数学原理(转) - TIMLONG - 博客园 (cnblogs.com)

至此，如何进行矩阵乘的节点求导就OK了。

def backward(self, dout):
 	W, = self.params
 	dx = np.dot(dout, W.T)
 	dW = np.dot(self.x.T, dout)
 	self.grads[0][...] = dW
 	return dx

小伙伴可以取手写pytorch中的一些自动求导了，设置好函数栈，将一些会变换梯度的节点一一入栈，然后一一出栈，按照事先写好的backward函数进行反向传播。

这里我们没有写一个激活函数求导，因为他们的导数都是具有特殊性的，需要一个一个写对应类。主要也就是forward和backward函数。

上面有一个细节，也就是X 由 1*D变成了N*D，这里就考虑到了小批量梯度下降算法，但是在数据处理这里就要注意了，batch_size需要自适应，还是需要初始化定义。推荐直接参考pytorch中的不够一个batch_size就直接舍弃这些数据。虽然不友好，但是入门快啊。

好吧，后面的深度学习还是任重而道远啊，毕竟这些玩意现在的框架都解决的很ok了。