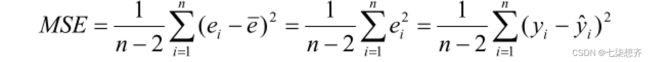数据预处理，插值拟合及回归分析

一.预处理

1.预处理应用

即使数据没有缺失值或者异常值也要进行数据预处理。大数据类型或者机器学习类一定要进行预处理。

2.数据处理

2.1  数据清洗——缺失值和异常值的处理

  2.1.1 缺失值处理：删除记录，数据插补或者不处理。最常见的是插补。

   1） 均值/中位数/众数插补，用这些值代替缺失值。

   2）固定值插补，有的属性值可以用常值代换。

   3）最近邻插补，用邻近的数插补（有时间顺序的情况），如果没有时间顺序，可以用欧几里得距离来衡量邻近。

   4）回归法——不建议用在国赛，运算量大。

   5）插值法

         i) 拉格朗日插值法——每次插值进去方程都要改变运算麻烦。

         ii) 牛顿插值法——与插值项数无关。

  2.1.2 异常值——主要是发现异常值的方法

    1) 高中的3 sigma 原则

    2) 箱型图

2.2  数据集成——多个数据表格相关联数据可以进行合并

2.3  数据归约——聚集或者删除冗余数据来压缩数据

2.4  数据变换——有的时候需要规范化

  2.4.1 偏态的数据很难表示，可以通过一些简单的函数变换像取对数，取指数从而达到一个类似标准的正态分布图，易于表示。

  2.4.2 归一化，即将数据都转化到0-1范围内，一般用于像机器学习中数据出现明显的数量级差异时。

3.数据工程

    数据工程包括数据预处理，特征处理，特征选择等等，一般需要做的是数据预处理，像特征选择使用较少，如遇到了随时间变化的数据可以进行特征选择。（不是很常用）

二.插值

注：1）所有的插值都要求x是单调的且插值的范围不得超过x定义域范围。

       2）已知函数在该区间内若干点的值求函数在该区间内其他点的值时，适宜用插值法解决。 

       3）利用多项式构建插值关系时，该多项式是唯一的，但是拟合的话不是唯一的。

       4）拟合可以看成插值的延申，已知1到12小时的销售额求1.5小时的销售额是插值问题，求13小时的销售额是拟合问题，两者各有适用范围。

1.一维插值

1.1 拉格朗日插值

解释：假设已知三个点，我们想构建插值多项式，三个点可以选取二次函数，如果直接构建比较困难，考虑做出函数L1(x),满足L1(x1)=1,且L1(x2)=0,L1(x3)=0,同理构建L2（x），使L2(x2)=1，另外两个值为0，构建L3（x),使L3（x3)=1，另外两个为0，则过三个点的函数为f(x)=y1L1(x) +y2L2(x)+y3L3(x),满足过三个点。

推广：

注：yi后的一堆记为Li(x),称为拉格朗日插值基函数。 选取不同的插值节点n+1个，n是插值多项式的次数。

缺点：插值次数大于七次时容易出现Runge现象，即在插值边缘出现严重的数据震荡。

改进：避免Runge现象的常用方法是分段低次插值，如样条函数插值。一次插值多用样条插值，二次插值多用立方插值。

1.2 分段线性插值

将每相邻两个节点用直线连接起来，如此形成的折线就是分段线性插值函数。

e.g：用分段线性插值法求插值，在[-6,6]中平均选41个点。

 matlab程序代码如下：

x=linspace(-6,6,100);
y=1./(x.^2+1);
x1=linspace(-6,6,41);
y1=1./(x1.^2+1);
plot(x,y,x1,y1,x1,y1,'o','LineWidth',1.5);
gtext('n=40');

plot函数中输入了两次x1,y1,对比一下前后的作图：
输入两次                                                                      输入一次

 即输入两次会将插值选到的两个点之间用线连接起来，而写一次的话只会标出点，不会连起来。

或者使用matlab自带的一维插值函数interp1(x0,y0,x,'method'),后面的方法有很多种选择，'nearest’  最邻近插值；‘linear’   线性插值；‘spline’ 三次样条插值；‘cubic’  立方插值；'pchip'同'cubic'，表示三次Hermite多项式插值；省略时 分段线性插值。

x=linspace(-6,6,100);
y=1./(x.^2+1);
x1=linspace(-6,6,41);
v=interp1(x,y,x1);
plot(x,y,x1,v,x1,v,'o','LineWidth',1.5);
gtext('n=40');

 注：gtext指的是对于做出来的图，鼠标点在哪里字符串就放在哪里。LineWidth指的是线宽。

其实分段插值有点像化直为曲，不断逼近的感觉（自我理解）

1.3 三次样条插值

样条插值更具有光滑性。matlab中也有现成的interp1(x0,y0,x,'spline')

三次样条插值，提倡使用csape函数,通常表示为pp=csape（x,y,conds,valconds)，y=ppval(pp,x),注意要用pp形式，ppval表示的是y的返回值。

2.二维插值

插值节点为网格节点

2.1 最邻近插值

2.2 分片线性插值

2.3 双线性插值

matlab的运用：

1）z=interp2(x0,y0,z0,x,y,’method’)

其中'nearest’ 最邻近插值；‘linear’  双线性插值；‘cubic’   双三次插值；缺省时双线性插值。

2）要求x0,y0单调；x，y可取为矩阵，或x取行向量，y取为列向量。

e.g:

试用二维插值法求出x,y间隔都为50的高程并画出等高图。 

x=0:400:5600;
y=0:400:4800;
z=[370 470 550 600 670 690 670 620 580 450 400 300 100 150 250;...
      510 620 730 800 850 870 850 780 720 650 500 200 300 350 320;...
      650 760 880 970 1020 1050 1020 830 900 700 300 500 550 480 350;...
      740 880 1080 1130 1250 1280 1230 1040 900 500 700 780 750 650 550;...
      830 980 1180 1320 1450 1420 1400 1300 700 900 850 840 380 780 750;...
      880 1060 1230 1390 1500 1500 1400 900 1100 1060 950 870 900 930 950;...
      910 1090 1270 1500 1200 1100 1350 1450 1200 1150 1010 880 1000 1050 1100;...
      950 1190 1370 1500 1200 1100 1550 1600 1550 1380 1070 900 1050 1150 1200;...
      1430 1430 1460 1500 1550 1600 1550 1600 1600 1600 1550 1500 1500 1550 1550;...
      1420 1430 1450 1480 1500 1550 1510 1430 1300 1200 980 850 750 550 500;...
      1380 1410 1430 1450 1470 1320 1280 1200 1080 940 780 620 460 370 350;...
      1370 1390 1410 1430 1440 1140 1110 1050 950 820 690 540 380 300 210;...
      1350 1370 1390 1400 1410 960 940 880 800 690 570 430 290 210 150];

figure(1);
meshz(x,y,z)
xlabel('X'),ylabel('Y'),zlabel('Z')

xi=0:50:5600;
yi=0:50:4800;

figure(2)
z1i=interp2(x,y,z,xi,yi','nearest');
surfc(xi,yi,z1i)
xlabel('X'),ylabel('Y'),zlabel('Z')

figure(3)
z2i=interp2(x,y,z,xi,yi');
surfc(xi,yi,z2i)
xlabel('X'),ylabel('Y'),zlabel('Z')

figure(4)
z3i=interp2(x,y,z,xi,yi','cubic');
surfc(xi,yi,z3i)
xlabel('X'),ylabel('Y'),zlabel('Z')


figure(5)
subplot(1,3,1),contour(xi,yi,z1i,10,'r');
subplot(1,3,2),contour(xi,yi,z2i,10,'r');
subplot(1,3,3),contour(xi,yi,z3i,10,'r');

 

注：contour是等高线函数，其中的数字代表等高线的条数。 

surf与mesh都是曲面，不同的是mesh只是将这些网格点连起来（见图一感觉），而surf是将整个曲面涂上颜色（见图二）。

surfc,meshc是在生成曲面的下方，同时生成等高线图（图二的x-y平面上就有等高线图）

surfz,meshz是生成曲面的同时，生成垂帘的感觉（见图一z轴的感觉）

插值节点为散乱节点

插值函数griddata格式为:  cz =griddata（x，y，z，cx，cy，‘method’），method同上。

要求cx取行向量，cy取列向量。

e.g：

x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=-[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
xi=75:1:200;
yi=-50:1:150;
zi=griddata(x,y,z,xi,yi','cubic');
subplot(1,2,1),plot(x,y,'*');
subplot(1,2,2),mesh(xi,yi,zi);

三.回归分析

1.回归分析与拟合的关系

回归分析是一种统计学上分析数据的方法，目的在于了解两个或多个变量间 是否相关，相关方向与强度，并建立数学模型以便观察特定变量来预测研究者感兴趣的量。拟合在某种程度上是承认了变量只见存在相关关系的，而回归则还要分析是否相关。 所以可以把关系总结为：拟合是回归分析中分析变量相关方向与相关强度的一种方法。（不一定正确哈）

2.一元线性回归分析

2.1 简介

注：E=0即随机误差的期望为零，方差为^2，是随机误差 ，回归直线方程中忽略掉了。

      有了回归直线方程，可以进行预测或者控制。

2.2 主要过程

2.2.1概述

1）用样本值对，及做点估计。

2）对回归系数，做假设检验。

3）在x=x0处对y做预测并进行区间估计。

 2.2.2 回归系数，的最小二乘法估计 

  求两者之间的关系，若为线性，只需要两组数据即可，可一般会有多于两组数据，所以导致会求出几组 ，。怎样抉择哪组是最好的，我们一般选择最小二乘法判断。

即两者之间的平方和之差最小

根据极值条件，Q对，的偏导为0时取极值。

但是求导适用于连续函数，而我们的点是离散的点，可以直接用吗？

答案是可以的，有最小二乘估计参数的离差形式。

这样求出的两个值，叫做最小二乘估计量。

 2.2.3 回归方程的显著性检验  

前面我们假设回归系数 是存在的，即符合线性关系，但是回归系数不一定存在，我们在进行回归之前需要先进行检验。假设H0:=0;H1:0

1）F检验法

 注:  F(n1.n2)指分子自由度为n1,分母自由度为n2的分布。F1-（1，n-2)是查表得到的，一般取为0.05，其中Qe=残差ei^2在i=1到n的求和。

       如果F大于表中值，代表这个线性关系很好，可以用，反之，则不好。当然即使F检验通过了也不一定说明模型恰当。

2）t检验法——适用于样本数相对较少，30个左右及以下的情况。

注: 即残差的样本标准差，方差记作MSE。MSE=Qe/(n-2)也等于下式。

                               

在一元线性分析中，t检验与F检验等价，但是在多元线性分析中，通常先进行F检验再进行t检验。

3) r检验法 

 2.2.4 回归方程的置信区间

求出与 也不一定正确，他们在一定的区间内我们才认同。

与置信水平1-的置信区间为

 ^2的置信水平为1-的置信区间为

 3.可线性化的一元非线性回归

 4.多元回归

 4.1多元线性回归

4.1.1定义

   一般称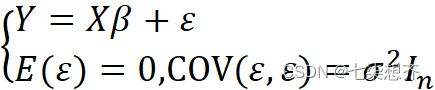  为高斯‑马尔可夫线性模型(k元线性回归模型)，并简记为(Y,Xβ,σ2In)                                                                                                                                 

  称为回归平面方程。

4.1.2模型参数估计

用最小二乘法求β0,...,βk的估计量，作离差平方和

           

选择β0,...,βk使Q达到最小．

 4.1.3 显著性检验

1）F检验法

H0:β0=β1=⋯=βk=0 

当H0成立时，

  。

如果F > F1-α（k，n-k-1），则拒绝H0，认为y与x1,…, xk之间显著地有线性关系；否则就接受H0，认为y与x1,…, xk之间线性关系不显著。

2）r检验法

定义为y与x1,x2,...,xk的多元相关系数或复相关系数。

4.2 多项式回归

  设变量x、Y的回归模型为

其中p是已知的，是未知参数，服从正态分布.

称为回归多项式，该模型称为多项式回归。

5.逐步回归

1）从一个自变量开始，视自变量Y对作用的显著程度，从大到小地依次逐个引入回归方程.

2）当引入的自变量由于后面变量的引入而变得不显著时，要将其剔除掉.

3）引入一个自变量或从回归方程中剔除一个自变量，为逐步回归的一步.

4）对于每一步都要进行Y值检验，以确保每次引入新的显著性变量前回归方程中只包含对Y作用显著的变量.

5）这个过程反复进行，直至既无不显著的变量从回归方程中剔除，又无显著变量可引入回归方程时为止.

6.matlab工具箱

6.1 多元线性回归

6.1.1线性回归的命令

   [b, bint,r,rint,stats]=regress(Y,X,alpha)

 

  b返回回归系数的点估计值，bint返回回归系数的置信区间矩阵，r返回残差组成的向量，rint返回矩阵包含可用于诊断离群值的区间，stats返回向量stats，包括相关系数r^2、F值、与F 对应的概率p。alpha缺少时代表显著性水平为0.05。X第一列都是1。

  相关系数r^2越接近1，说明回归方程越显著。 F > F1-α（k，n-k-1）时拒绝H0，F越大，说明回归方程越显著；与F对应的概率p<α时拒绝H0，回归模型成立。

6.1.2画出残差及其置信区间

     rcoplot（r，rint）

6.2 多项式回归

6.2.1一元多项式回归

1） [p，S]=polyfit（x，y，m）

  其中x=（x1，x2，…，xn），y=（y1，y2，…，yn），p=（a1，a2，…，am+1）是多项式y=a1xm+a2xm-1+…+amx+am+1的系数；S是一个矩阵，用来估计预测误差，m是拟合多项式的次数。

  Y=polyval（p，x）

  求polyfit所得的回归多项式在x处的预测值Y；

 [Y，DELTA]=polyconf（p，x，S，alpha）

   求polyfit所得的回归多项式在x处的预测值Y及预测值的显著性为1-alpha的置信区间Y +-DELTA。alpha缺省时为0.5。

2）polytool（x，y，m）

6.2.2多元二项式回归

rstool（x，y，’model’, alpha）

x是n*m的矩阵，y是n维矩阵，alpha缺少时是0.05，model由下列4个模型中选择1个（用字符串输入，缺省时为线性模型）：

linear（线性）：

purequadratic（纯二次）：

interaction（交叉）：

quadratic（完全二次）：

6.3非线性回归

6.3.1 确定回归系数

               [beta，r，J]=nlinfit（x,y,’model’,beta0）

输入数据x．y分别为  矩阵和n维列向量，对一元非线性回归，x为n维列向量.model是事先用M文件定义的非线性函数，beta0是回归系数的初值，随便赋一个。

6.3.2非线性回归命令

              nlintool（x，y，’model’, beta0，alpha)

6.3.3 预测和误差估计

[Y，DELTA]=nlpredci（’model’, x，beta，r，J）

求nlinfit 或lintool所得的回归函数在x处的预测值Y及预测值的显著性水平为1-alpha的置信区间

 6.4 逐步回归

         stepwise（x，y，inmodel，alpha）

x是自变量数据n*m阶矩阵，y是因变量数据n*1阶矩阵。inmodel是矩阵的列数的指标，给出初始模型中包括的子集（缺省时设定为全部自变量）

在Stepwise  Plot窗口，显示出各项的回归系数及其置信区间。

Stepwise Table 窗口中列出了一个统计表，包括回归系数及其置信区间，以及模型的统计量剩余标准差（RMSE）、相关系数（R-square）、F值、与F对应的概率P。

四.拟合

1.与插值的关系

插值主要求函数值，拟合主要求函数关系。插值过所有点，拟合不一定过所有点

2.适用范围

小范围做预测，或者x与y关系不能直接得到，需要求导

3.matlab拟合

3.1 cftool工具箱

matlab中cftool拟合工具箱可以很好的解决拟合问题。

SSE或RMSE如果数值不是很大，不超过0.1，说明拟合效果很好。

先输入数据，然后输入cftool召唤工具箱，一般用的比较多的是多项式拟合，功能强大。

3.2 函数拟合

3.2.1 多项式线性拟合

函数使用同多项式回归

a=polyfit(x,y,m)，a是多项式系数

y=polyval（a，x）多项式在x处的值

e.g:对下面这组数据进行二次多项式拟合

xi	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1
yi	-0.447	1.978	3.28	6.16	7.08	7.34	7.66	9.56	9.48	9.30	11.2

函数求解

 

 

或者cftool

 3.2.2 非线性多项式拟合

1）lsqcurvefit

数据点：  xdata=（xdata1,xdata2,…,xdatan）,ydata=（ydata1,ydata2,…,ydatan）  

x=lsqcurvefit(‘fun’,x0,xdata,ydata,options)

fun是一个事先建立的定义函数F(x,xdata) 的M文件, 自变量为x和xdata，opotions同无约束优化。

2）lsqnonlin

x= lsqnonlin （‘fun’，x0，options）