2.4 PIMPLE算法 | 2.5 附加显式力的压力速度耦合(OpenFOAM理论笔记系列)
2.4 PIMPLE算法
2.4.1速度的非线性耦合
在2.1节中,我们曾对流动系统的压力速度耦合问题进行过讨论,实际上,在流动系统中除了压力和速度的耦合关系,我们还存在着另一种重要的耦合关系,速度的非线性耦合关系。当我们对速度进行求解时(例如求解动量预测方程),速度是未知量,因此对流项 ∇ ⋅ ( U ⃗ U ⃗ ) \nabla\cdot(\vec U\vec U) ∇⋅(UU)是一个未知量乘以未知量的结果,这样会使得原来呈线性的方程变为非线性方程(即未知数的最高次数从1变为2)。直接求解非线性系统的矩阵方程需要调用非线性求解器,然而非线性求解器相对线性求解器来说相对复杂,计算成本较高。在实际中,我们一般对非线性项进行线性化处理:
我们回顾以下之前对对流项的离散过程:
∫ V P ∇ ⋅ ( ρ ϕ U ⃗ ) d V = ∑ f [ S f ⋅ ( ρ ϕ U ⃗ ) f ] = ∑ f [ S f ⋅ ( ρ U f ⃗ ) ϕ f ] = ∑ f ( F ϕ f ) (1.28) \int_{V_P}\nabla\cdot(\rho\phi\vec U) dV=\sum_f\left[ {S_f}\cdot\left(\rho\phi\vec U\right)_f\right]=\sum_f\left[ {S_f}\cdot(\rho\vec {U_f})\phi_f\right]\\=\sum_f(\mathbf{F}\phi_f) \tag{1.28} ∫VP∇⋅(ρϕU)dV=f∑[Sf⋅(ρϕU)f]=f∑[Sf⋅(ρUf)ϕf]=f∑(Fϕf)(1.28)
上式中 F = S f ⋅ ( ρ U f ⃗ ) \mathbf{F}={S_f}\cdot(\rho\vec {U_f}) F=Sf⋅(ρUf)为质量通量(mass flux)。
为了与相关文献中的表述一致,在本节后,我们不再使用字母 ϕ \phi ϕ表示任意标量,而表示通量,在未加下标的情况下, ϕ \phi ϕ默认表述速度的通量 ϕ = S f ⋅ U f ⃗ \phi={S_f}\cdot\vec {U_f} ϕ=Sf⋅Uf。仿照式1.28,对于NS方程中的对流项我们可以进行如下的离散:
∫ V P ∇ ⋅ ( U ⃗ U ⃗ ) d V = ∑ f [ S f ⋅ ( U ⃗ U ⃗ ) f ] = ∑ f ( S f ⋅ U f ⃗ ⋅ U f ⃗ ) = ∑ f ( ϕ U f ⃗ ) (2.25) \int_{V_P}\nabla\cdot(\vec U\vec U) dV=\sum_f\left[ {S_f}\cdot\left(\vec U\vec U\right)_f\right]=\sum_f\left( {S_f}\cdot\vec {U_f}\cdot\vec{U_f}\right)\\=\sum_f(\phi \vec{U_f}) \tag{2.25} ∫VP∇⋅(UU)dV=f∑[Sf⋅(UU)f]=f∑(Sf⋅Uf⋅Uf)=f∑(ϕUf)(2.25)
所谓线性化处理,指的是使用当前步已知的速度去计算式(2.25)中的通量,即将之前的未知量乘积项 ∇ ⋅ ( U ⃗ n U ⃗ n ) \nabla\cdot(\vec U^n\vec U^n) ∇⋅(UnUn)转化为 ∇ ⋅ ( U ⃗ o U ⃗ n ) \nabla\cdot(\vec U^o\vec U^n) ∇⋅(UoUn),相应的离散结果由 ∑ f ( ϕ n U f n ⃗ ) \sum_f(\phi^n \vec{U_f^n}) ∑f(ϕnUfn)转变为 ∑ f ( ϕ o U f n ⃗ ) \sum_f(\phi^o \vec{U_f^n}) ∑f(ϕoUfn)。
显然,将对流项进行线性化是不精确的,其会导致通量信息的滞后。
2.4.2 SIMPLE和PISO算法的讨论
在这一节,我们将讨论对流项的线性化处理对于SIMPLE算法和PISO算法带来的影响。
首先,我们需要搞明白线性化后对流项中的滞后通量 ϕ o \phi^o ϕo最终作用在了哪里。观察式(2.25),对流项最终转化为了滞后通量 ϕ o \phi^o ϕo与面上速度 U f n ⃗ \vec{U_f^n} Ufn乘积的形式,而在1.3.3节我们知道,面上的速度值最后通过引入对流项离散格式转化为当前网格体心速度值 U ⃗ p n \vec U_p^n Upn与相邻网格体心速度值 U ⃗ p n \vec U_p^n Upn的组合。因此,滞后的通量最终作用在了最终离散方程中 U ⃗ p n \vec U_p^n Upn与 U ⃗ p n \vec U_p^n Upn的系数,即式2.1中的 a P a_P aP与 a N a_N aN上。
无论是SIMPLE算法还是PISO算法,我们依赖 a P a_P aP与 a N a_N aN计算 H b y A HbyA HbyA并求解压力泊松方程,而一旦动量方程建立, a P a_P aP与 a N a_N aN的值就确定了下来(见2.1节对于H算符和 H b y A HbyA HbyA算符的矩阵解释),如果要更新 a P a_P aP与 a N a_N aN就必须带入新的速度值建立动量方程。从OpenFOAM的代码角度来说,组建一次fvVectorMatrix UEqn就相当于以当前得到的速度更新了一次 a P a_P aP与 a N a_N aN,即更新了一次滞后的通量。
考虑稳态的SIMPLE算法,其在每一个迭代步内进行计算时,都会重新组建一次动量方程进行动量预测(是否进行动量预测步骤并不重要,重要的是其重新组建了一次动量方程),因此其滞后的通量值会在下一次迭代开始的时候进行更新。当最终模拟收敛的时候,迭代步内的 U o = U n U^o=U^n Uo=Un,线性化后的 ∇ ⋅ ( U ⃗ o U ⃗ n ) \nabla\cdot(\vec U^o\vec U^n) ∇⋅(UoUn)还原为 ∇ ⋅ ( U ⃗ n U ⃗ n ) \nabla\cdot(\vec U^n\vec U^n) ∇⋅(UnUn),非线性项得到完全求解。
我们再来考虑瞬态的PISO算法,通过2.3.1节的分析我们可以发现,在每一个时间步内,PISO算法只进行了一次动量方程的组建,因此在每个时间步内对流项中的通量始终是滞后的,第n步时间步求解的对流项只能是 ∇ ⋅ ( U ⃗ n − 1 U ⃗ n ) \nabla\cdot(\vec U^{n-1}\vec U^n) ∇⋅(Un−1Un),当然,如果系统最终可以达到稳态,速度不再变化,那么PISO算法还是能够收敛到正确的稳态值。
既然对流项的线性化处理使得PISO算法每一步的通量产生了滞后,那为什么还可以使用PISO算法来计算瞬态问题呢?事实上,在瞬态计算中,时间步长的步进往往非常小,这就意味着两个相邻时间步的速度更新很小,速度之间的非线性耦合较弱,PISO算法认为此时可以忽略通量滞后带来的误差,专注于处理压力速度之间的耦合问题。事实上,自PISO算法提出后进行的众多的模拟实践也表明这种忽略是可以接受的。
2.4.3 OpenFOAM中的PIMPLE算法
正如在上一节中所述,PISO算法可以忽略滞后通量影响的前提是相邻两个时间步速度场的变化不大,这就要求进行瞬态模拟时必须采用较小的时间步长。对于时间步长较大的模拟,采用PISO算法往往会造成模拟崩溃。为了解决这个问题,OpenFOAM发展了一种PISO算法与SIMPLE算法混合的PIMPLE算法。
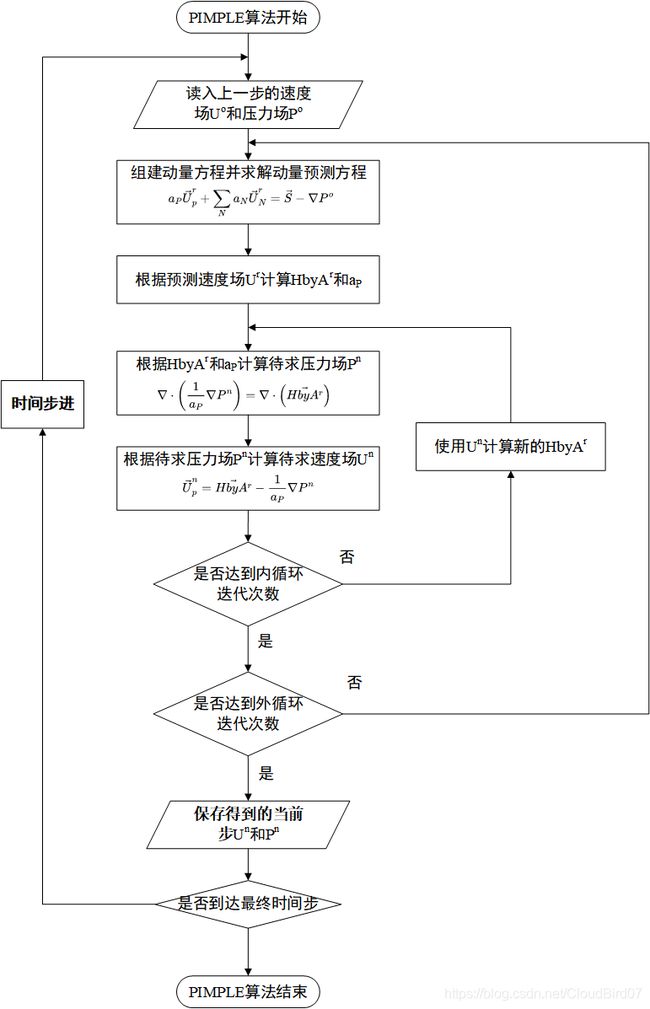
PIMPLE算法非常类似于瞬态版本的SIMPLE算法,有兴趣的读者可以按照2.2节的指引阅读相关文献。简单来说,PIMPLE算法在PISO算法的基础上在外层添加了一个类似SIMPLE算法的外循环进行动量方程的重建。每进行一次动量方程的更新,都会将原本滞后的通量进行更新,因此PIMPLE算法能够较好地处理大时间步长下的瞬态计算。其算法框图如下;
PIMPLE算法是PISO和SIMPLE算法的结合体,由于之前在SIMPLE和PISO算法的介绍中已经对代码进行了较为详细的解读,因此在这里就不详细进行介绍了。PIMPLE算法中的设置主要在fvsolution字典中的PIMPLE子字典中进行,其需要设置的项为PISO和SIMPLE算法中所有要设置项的集合,读者可以参考前面的章节。
PIMPLE算法没有原始文献可以参考,但文献1对PISO算法和SIMPLE算法进行了较为详细的对比分析,对于理解PIMPLE算法很有帮助,感兴趣的读者可以阅读。
2.5 附加显式力的压力速度耦合
在CFD实践中,向动量方程中附加诸如重力,表面张力,电磁力等显式力(即求解动量方程时力的大小已知)是一类常见的操作。在本节,我们将详细探讨如何在PISO,SIMPLE这类压力速度耦合算法中附加显式的体积力。
我们首先定义附加的显式体积力为 F ⃗ \vec F F。需要注意的是,如果求解的是形如式(1.5)的将密度约去的动量方程,则我们应该附加的是真实体积力除以密度得到的商,如果求解的是完整的包含密度的动量方程,直接植入完整的体积力即可。考虑 F ⃗ \vec F F后,动量方程的离散结果可以写为:
a P U ⃗ p n + ∑ N a N U ⃗ N n = S ⃗ − ∇ P n + F ⃗ (2.26) a_P\vec U_p^n+\sum_Na_N\vec U_N^n=\vec S-\nabla P^n+\vec F \tag{2.26} aPUpn+N∑aNUNn=S−∇Pn+F(2.26)
此时对 F ⃗ \vec F F有两种处理的思路,第一种处理思路是将 F ⃗ \vec F F与源项 S ⃗ \vec S S组合在一起,即:
a P U ⃗ p n + ∑ N a N U ⃗ N n = S ⃗ F − ∇ P n (2.27) a_P\vec U_p^n+\sum_Na_N\vec U_N^n=\vec S_F-\nabla P^n \tag{2.27} aPUpn+N∑aNUNn=SF−∇Pn(2.27)
其中 S ⃗ F = S ⃗ + F ⃗ \vec S_F=\vec S+\vec F SF=S+F。这种植入方式最大的优势是简单,其没有改变速度的更新方程(2.4)和压力泊松方程(2.6)的形式,因此无需对压力速度耦合算法的过程进行大量修改。回归到OpenFOAM代码中,这种体积力植入方式仅需要在组建动量方程时添加一个力F源项而已:
- 代码3 外力在动量方程中的植入(方法1)
fvVectorMatrix UEqn
(
fvm::div(phi, U)
+ MRF.DDt(U)
+ turbulence->divDevReff(U)
//释: turbulence->divDevReff(U)即扩散项,因为湍流模型,流变模型等代码实际上是对扩散项进行修正,因此在OpenFOAM中扩散项的计算归于湍流模型的代码中。
==
fvOptions(U)+F
);
如果你要植入的体积力表达形式相对简单且你不想修改源代码,你可以使用OpenFOAM提供的源项功能在算例中进行设置,这相当于修改了上述代码中的fvOptions(U)。另外,如果你使用的是PIMPLE系列求解器,并且你要施加的外力是恒力,你甚至可以通过修改算例constant目录下的g字典来修改重力加速度的值来用改变重力的方法植入你需要的外力。
除去将 F ⃗ \vec F F与源项 S ⃗ \vec S S组合在一起这一种思路,还有另外一种植入方法,即将 F ⃗ \vec F F与压力整合在一起考虑而并不归入源项。在这种思路下,速度的更新方程(2.4)和压力泊松方程(2.6)将演化为:
U ⃗ p n = H b y A n ⃗ − 1 a P ( ∇ P n − F ⃗ ) (2.28) \vec U_p^n=\vec{HbyA^n}-\frac{1}{a_P}\left(\nabla P^n-\vec F\right) \tag{2.28} Upn=HbyAn−aP1(∇Pn−F)(2.28)
∇ ⋅ ( 1 a P ∇ P n ) = ∇ ⋅ ( H b y A n ⃗ + 1 a P F ⃗ ) (2.29) \nabla\cdot\left(\frac{1}{a_P}\nabla P^n\right)=\nabla\cdot\left(\vec{HbyA^n}+\frac{1}{a_P}\vec F\right) \tag{2.29} ∇⋅(aP1∇Pn)=∇⋅(HbyAn+aP1F)(2.29)
将形式改变后的各式带回各压力速度耦合算法,即可得到植入外力后的新的压力速度耦合算法。
使用第二种思路需要按照如下的方式修改对应的OpenFOAM代码:
首先修改动量预测方程。注意,此时不能在动量方程组建时额外植入力,否则将变成方式1的植入方法。我们在求解动量预测方程的步骤添加外力:
- 代码4 外力在动量方程中的植入(方法2)
if (pimple.momentumPredictor())
{
solve(UEqn == -fvc::grad(p))+F;
}
由于我们改变了速度更新方程和压力泊松方程的形式,因此我们也应该修改代码中对于压力方程的的求解部分,对于大部分求解器,此部分代码在pEqn.H中。读者自然可以按照各个方程的对应关系来修改代码,但这里我更倾向于使用一种简单的方式。OpenFOAM中大部分求解器都是耦合重力的求解器,而重力本身就是一个附加的体积力,因此我们仅需向重力的耦合代码中加入我们自己的力即可,具体来说,修改pEqn.H中的如下代码:
- 代码5 外力在压力方程中的植入(方法2)
surfaceScalarField phig
(
- ghf*fvc::snGrad(rho)*rAUf*mesh.magSf()+rAUf*fvc::flux(F)
);
在上述代码中,我们在重力的通量中添加了我们的外力通量rAUf*fvc::flux(F)。当然,你也可以去研究重力通量phig在之后的代码中如何起作用,phig的植入方式是标准的按照方式2进行的植入,我们在这里将F的作用归入重力中,因此就无需修改后面的代码了。
上述两种植入方法在OpenFOAM中均有实例。在磁流体求解器mhdFoam中,磁场力的植入方式是按方式1进行的,在PIMPLE系列求解器中,重力是按方式2植入的,在inter系列求解器中,表面张力也是按照方式2进行植入的。笔者曾经测试过对于同一个外力使用两种植入方式对于求解的差异,二者在瞬态的每个时间步内有微小的差异,但最终都可以收敛到相同的稳态结果。造成这种差异的原因笔者还没有进行深入研究,就个人直觉来看,笔者认为凡是可以写成某个量的梯度的力(例如表面张力可以写成相分数梯度的函数,重力可以写成密度梯度的函数)应该按方式2进行植入,不能写成梯度函数的力应该按方式进行植入,但这仅是个人猜测,感兴趣的读者可以自行深入研究。
在这里我们必须重新强调一下OpenFOAM计算HbyA等方程系数的方法。在OpenFOAM中,除去压力和其他源项的动量方程首先被整理成一个矩阵系统(即fvVectorMatrix UEqn),各项系数都是根据这个矩阵系统求得的(例如UEqn.A()计算得到了 A p Ap Ap,可参考代码1)。如何根据矩阵系统求得各项系数可以参考(2.1)节。一个矩阵系统求得的系数是唯一的,因此,如果需要修改HbyA等的值,就必须重新组建矩阵系统(即重新建立一个fvVectorMatrix UEqn)。在这节我们所述的方法一中,方程系数 S ⃗ \vec S S被改变,因此我们修改了初始化UEqn的代码(代码3)。在方法二中,我们将外力与压力放在一起处理,动量方程离散后的各系数没有变化,因此我们在动量方程中没有在UEqn初始化的部分进行F的植入,而是在求解UEqn时在等号右侧进行植入(代码4),此时并不会影响UEqn的结构。
由于植入方法一相对来说比较常见,因此很多对代码和理论不熟悉的初学者会在听别人说植入外力就是向动量方程中添加一项后仅仅进行代码4的植入。这种植入方法显然是错误的,各位读者不妨结合本节所述内容自行思考一下这样的植入本质上对压力速度耦合算法产生了什么影响。
系列说明:
接触有限体积法有一段时间了,也看了一些资料,但是有时候总觉得看过一遍之后什么也记不住。老话说得好,眼过千遍不如手过一遍,久而久之我就有了写一些比较像样子的笔记的想法。初学的时候曾经写过一本叫“OpenFOAM编程笔记:单相不可压缩流动”的册子,但当时基础太差(现在基础也不好),错误太多,倒不如推倒重来。
本系列将持续更新,欢迎各位挑错交流,挑错交流可以直接留言也可以联系邮箱cloudbird7@foxmail.com。等到预定内容全部写完后我将集结所有内容为一个独立的文件,开放下载。
Barton I E . Comparison of simple- and piso-type Algorithms for Transient Flows[J]. International Journal for Numerical Methods in Fluids, 2015, 26(4):459-483. ↩︎