万字长文教你优化轻量姿态估计模型(算法篇),附调参侠秘籍!
本文来自社区投稿,作者知乎 ID:镜子
0. 观前提醒
在本文中你将会看到:
- 【CPU 下 12ms】轻量姿态估计模型 Regression 方法如何做到比 Heatmap 方法快近 3 倍且精度更高
- 【集中盘点】轻量模型常规涨点 trick 总结
- 【调参侠秘籍】在无参可调的情况下如何找到可以调的参数
- 【搬砖心得】项目工程经验分享
- 【爬坑记录】一些没有起到效果的技术
用充分的实验告诉你,为什么在工程落地中 Regression 方法是比 Heatmap 更好的选择。
本文中所有的实验均基于 MMPose,本文中所有涉及的内容都会逐一迭代进 MMPose 开源库中,欢迎大家体验 MMPose,基于 MMPose 可以轻松复现各种新方法。
MMPose 是一款基于 PyTorch 的姿态分析的开源工具箱,是 OpenMMLab 项目的成员之一。
https://github.com/open-mmlab/mmposegithub.com/open-mmlab/mmpose
1. 前言
在上一期中我初步体验了 MMPose,牛刀小试之后,接下来就应该真正动手做一些自己的东西了。
镜子:mmpose初体验:推理、导出ONNX、转MNN19 赞同 · 4 评论文章正在上传…重新上传取消
凭借 MMPose 优秀的实验配置管理系统,我打算建立一组公平的消融实验对比,向大家展示各种方法在轻量模型上的优劣,以及在实际项目优化中我会如何思考和取舍。
严格来说这篇文章已经不算是 MMPose 的学习笔记了,而是基于 MMPose 做实验的记录,这个过程让我对 MMPose 的运用熟练了很多,在此需要感谢 MMPose 社区大佬和小伙伴们的热心解答。
还记得年初 ConvNeXt 问世时,那张优化路径图给我留下了很深的印象,想着总有一天我也要这么搞一次,于是有了这张图:
本文标题为算法篇,因此写作的核心是围绕算法进行的模型优化,而在真正做项目落地的过程中,优化是全方位的,因此还会有部署篇、数据篇、工程篇等等,以后有机会的话我也会进行总结。
为了完成这篇文章我在自己的单卡机器上训了几十个实验,前后肝了一个多月,可谓呕心沥血,希望大家能给我点个赞鼓励一下,也欢迎关注我的公众号【镜子的掌纹】~
2. Baseline 搭建
2.1 编写配置文件
我计划搭建的 baseline 是 shufflenetv2+deeppose 方法,目前 MMPose 的库中暂时没有现成的配置脚本可以用。
去翻了翻文档里已有的模型记录,虽然当前 MMPose 并没有轻量模型+回归方法的 baseline,但我找到了 ResNet50+Regression 和 ShuffleNetV2+Heatmap 在 COCO 上的两个 baseline,所以我很自然地可以参考这两个配置文件来搭建我的目标。
从文档给出的 benchmark 可以看到,Heatmap 方法由于降低了学习难度,在 ShuffleNet 这样的轻量模型上性能都高于用 ResNet50 的 Regression 方法,这也是符合预期的:
接下来开始对比两个 config 文件:
由于两个方法的差异主要体现在模型结构上,其他大部分训练策略都是一样的,在 model 定义部分分别使用了 ShuffleNet 和 ResNet,可以看到 ShuffleNet 使用的是基于 MMClassification 的预训练参数,而 ResNet50 使用的是 Torchvision 官方的参数。
而决定输出关键点形式的模块 keypoint_head 一栏,分别用了 TopdownHeatmapSimpleHead 和 DeepposeRegressionHead,对应 Heatmap 和 Regression 头部,损失函数上 Heatmap 方法使用 MSELoss,Regression 用的 SmoothL1Loss。
接下来的 data_cfg 配置,由于我要在 MPII上 训练,所以 data_cfg 和 train_pipleline 按照 res50 上 mpii 的配置即可。
如此,一个 ShuffleNetV2 + Regression 在 mpii 上的配置文件也可以很快写出来。
同时按照 MMPose 的命名规则和文件结构存到configs/body/2d_kpt_sview_rgb_img/deeppose/mpii/ 路径下,命名为shufflenetv2_mpii_256x256.py 。
2.2 导出 ONNX 和 MNN
在完成配置后其实已经可以开始训练了,但是良好的工程习惯是应该先测试模型的导出部署和推理速度,确保这套流程能顺利进行且满足需求后再进行模型的训练。
目前 MMPose 在设计导出 ONNX 时的脚本还未考虑到这个需求,是强制要求输
checkpoint 进行参数加载的,所以需要对 tools/deployment/pytorch2onnx.py 做一点点的小修改,把强制参数改成可选参数,默认为 None:
# mmpose默认版本
parser.add_argument('checkpoint', help='checkpoint file')
# 修改为:
parser.add_argument('--checkpoint', default=None, required=False, help='checkpoint file') 然后就可以通过脚本导出 ONNX 文件了:
python tools/deployment/pytorch2onnx.py configs/body/2d_kpt_sview_rgb_img/deeppose/mpii/shufflenetv2_mpii_256x256.py --shape 1 3 256 256 得到 tmp.onnx 后照例进行一下 ONNX 结构简化:
python -m onnxsim tmp.onnx tmp-sim.onnx 之后也跟上一篇文章一样,把 ONNX 转成 MNN:
python -m MNN.tools.mnnconvert -f ONNX --modelFile tmp-sim.onnx --MNNModel tmp.mnn --fp16 --bizCode MNN
沿用上一篇文章里实现的 python 端 MNN 推理脚本:
import numpy as np
import MNN
import cv2
import time
class Pose():
def __init__(self, model_path, joint_num=21, mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]):
self.model_path = model_path
self.joint_num = joint_num
self.mean = np.array(mean).reshape(1, -1, 1, 1)
self.std = np.array(std).reshape(1, -1, 1, 1)
self.interpreter = MNN.Interpreter(model_path)
self.model_sess = self.interpreter.createSession({
'numThread': 1
})
def preprocess(self, img):
input_shape = img.shape
assert len(input_shape) == 4, 'expect shape like (1, H, W, C)'
img = (np.transpose(img, (0, 3, 1, 2)) / 255. - self.mean) / self.std
return img.astype(np.float32)
def inference(self, img):
input_shape = img.shape
assert len(input_shape) == 4, 'expect shape like (1, C, H, W)'
input_tensor = self.interpreter.getSessionInput(self.model_sess)
tmp_input = MNN.Tensor(input_shape,
MNN.Halide_Type_Float,
img.astype(np.float32),
MNN.Tensor_DimensionType_Caffe)
input_tensor.copyFrom(tmp_input)
self.interpreter.runSession(self.model_sess)
output_tensor = self.interpreter.getSessionOutputAll(self.model_sess)
joint_coord = np.array(output_tensor['1022'].getData())
return joint_coord
def post_process(self, coords, bbox):
w = bbox[2] - bbox[0]
h = bbox[3] - bbox[1]
target_coords = coords * np.array([w, h])
target_coords += np.array([bbox[0], bbox[1]])
return target_coords
def predict(self, img):
img = self.preprocess(img)
# print(img.shape)
joint_coord = self.inference(img)
# joint_coord = self.post_process(joint_coord)
return joint_coord
img = cv2.imread(r'D:\projects\mmpose\tests\data\onehand10k\9.jpg')
img = cv2.resize(img, (256, 256))
inputs = img[None,:]
mnn_model = Pose('tmp.mnn')
for x in range(5):
s = time.time()
for i in range(100):
mnn_model.predict(inputs)
print(f'elapse {(time.time() - s)*10:.4f} ms') 测试一下推理速度,在我本地 i5-12600KF 的 CPU 上推理是在 6ms 左右的:
$ python mnn_inference.py
elapse 7.1200 ms
elapse 7.0100 ms
elapse 6.7400 ms
elapse 6.7100 ms
elapse 6.6700 ms
确认了流程没问题后送去训练,为了实验稳定我锁定了随机种子:
python tools/train.py configs/body/2d_kpt_sview_rgb_img/deeppose/mpii/shufflenetv2_mpii_256x256.py --seed 1234
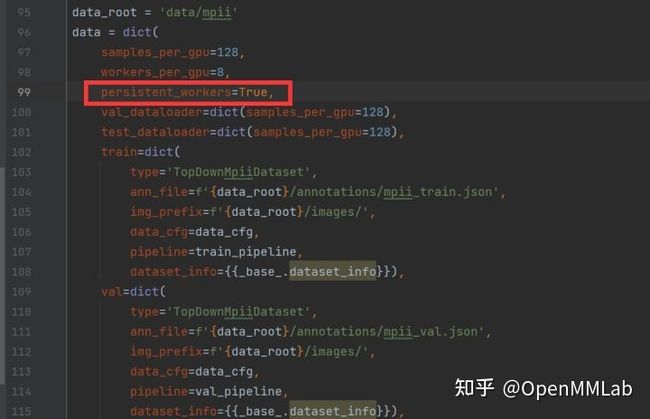
在训了几个 epoch 后我注意到,在每个 epoch 之间都会有一次 UserWarning 的输出,并且有个短暂停顿,根据经验我猜到是因为 Dataloader 没有开 persistent_workers,导致每个 epoch 都会重新启动多进程,很快我在 mmpose/datasets/builder.py 下找到了 Dataloader 的定义发现果然如此:
为了加速训练我开启了 persistent_workers,由于 MMPose 优秀的注册器机制,我可以在配置文件中直接手动添加这个参数,而不需要去修改 builder.py 文件:
2.3 RLE & Heatmap
有了第一个模型的经验后,RLE 和 Heatmap 都是现成的配置文件,如法炮制即可。
为了清晰地横向对比,所以我做了 ShuffleNetV2+Heatmap 的实验,考虑到 Heatmap 肯定在精度上有优势,但是存在速度劣势,所以我也导出了 Heatmap 的 MNN 模型进行了推理速度测试:
$ python mnn_inference.py
elapse 34.7578 ms
elapse 34.7508 ms
elapse 35.0740 ms
elapse 34.7600 ms
elapse 35.2101 ms
可以发现,Heatmap方法跟 Regression 方法相比,推理速度慢了接近 6 倍。而 RLE 方法由于只是在训练阶段添加了一个 flow 模型,在推理阶段直接扔掉,所以推理速度跟 Regression 方法是一样的。
2.4 实验小结一
在清楚了基本的训练流程后,采用完全相同的实验配置我做了如下四个实验,实验配置为:
- 单 GPU 3060 Ti
- bs=128 训练 210 epoch
- adam 上学习率 e-4,step=[170, 200]
- imagenet 预训练 backbone 参数
结果如下表:
表中带 * 表示 backbone 使用了基于 Heatmap 预训练的 backbone 权重:
deeppose:
"Head": 88.16508, "Shoulder": 88.4341, "Elbow": 70.78576, "Wrist": 56.23045, "Hip": 79.0895, "Knee": 61.17217, "Ankle": 49.71674
rle:
"Head": 81.71896, "Shoulder": 92.20448, "Elbow": 80.91024, "Wrist": 69.95078, "Hip": 84.68064, "Knee": 70.31898, "Ankle": 55.52689
heatmap:
"Head": 94.84993, "Shoulder": 92.71399, "Elbow": 83.56934, "Wrist": 75.99908, "Hip": 83.88427, "Knee": 77.67446, "Ankle": 71.53964
rle*:
"Head": 81.71896, "Shoulder": 92.56114, "Elbow": 81.72857, "Wrist": 71.2035, "Hip": 85.14798, "Knee": 71.97149, "Ankle": 57.0382
从实验结果可以看到,在轻量模型上:
- 原始的 Regression 方法精度最低
- 在加入了 RLE 方法后,Regression 精度得到了一个较大的提升(PCKh 上 6 个点)
- 不考虑计算效率的话,Heatmap 方法在轻量模型上效果还是最好的,但是推理耗时是 Regression 的 6 倍
- 用 Heatmap 训练后的模型 backbone 权重训练 RLE,精度能再进一步提升(PCKh 上 1 个点)
- 分辨率对于姿态估计任务非常重要,减小输入图片让 Heatmap 方法掉了 8 个点
另外不得不指出的一点:由于监督方式的不同,梯度形式上的差距使得 Heatmap 在训练效率上是远高于 Regression 方法的,这一点从训练 10 个 epoch 的表现就能体现:
- Heatmap 方法训练 10个 epoch 后 acc_pose 能达到 0.70
- Deeppose 方法只有 0.37
- 原始 RLE 方法训练 10 个 epoch 后 acc_pose 达到 0.41
- 使用预训练权重后 RLE 方法训练 10 个 epoch 的 acc_pose 达到 0.56
考虑到从头训练的 RLE 方法最终 acc_pose 为 0.717,我查询 log 后发现达到 0.70 的时间是在 100 epoch,也就是说在同样使用 imagenet 预训练的 backbone 参数情况下,Heatmap 方法训练 10 epoch 就得到了相当于 Regression 方法 100 epoch 的效果,这就是监督方式不同带来的训练效率差异,而我们要想提升 Regression 方法的性能,其中一个思路就是把更多的监督信息引入到训练中。
3. 参数量 & 监督信息
到目前为止,有了预训练权重和 RLE 加持,Regression 跟 Heatmap 的精度差距是 PCKh 上 4.2 个点,而 6 倍的速度差距给我了充足的算力空间,来进一步提升 Regression 的精度。
此时我有两个思路:
- 轻量模型之所以弱于大模型,首先是参数量上存在差距。6 倍的速度差距让我可以简单粗暴地增大 backbone 参数量,比如将 ShuffleNetV2 的宽度系数从 1.0 变为 2.0,推理速度也只是从 6ms 变成 15ms,仍然比 Heatmap 快 2 倍。
- 使用 Integral Pose Regression 方法,学习隐式的 Heatmap,有了更多可以引入监督信息的地方。
3.1 增大 backbone 参数量
增大 backbone 最简单的办法就是调整宽度系数,ShuffleNetV2 x2.0 后 Regression 推理速度如下:
elapse 16.6774 ms
elapse 15.7000 ms
elapse 16.4100 ms
elapse 15.9700 ms
elapse 16.5253 ms
最终训练结果如下:
"Head": 85.91405, "Shoulder": 94.20856, "Elbow": 84.42139, "Wrist": 75.15977, "Hip": 87.06935, "Knee": 77.39249, "Ankle": 64.12375, "PCKh": 82.82332, "PCKh@0.1": 23.9032
可以看到,跟 Heatmap 版本的差距已经非常小了,PCKh 上只相差 0.8 个 点,PCKh@0.1 超越了 2.6 个点,而推理速度比 Heatmap 快 2 倍。假如我继续加大 backbone 的缩放比例到 2.5 或者 3.0,应该是可以全面追平和超越 Heatmap 的,但这样并不是一个好的优化思路,由于低算力设备的 CPU 通常是远弱于台式机的,经常会出现慢 2-3 倍的情况,因此 15ms 差不多是本地测试可以接受的最低速度了,这样一来 backbone 直接占用了大部分算力,模型头部就没有任何可以优化的空间了。而实际在优化时,backbone 的优化通常是放在最后进行的。
这个实验的目的也主要是想告诉大家,推理速度的优势意味着可以增加更多的参数量,这对于轻量模型而言至关重要。
3.2 Integral Pose Regression
Integral Pose Regression 方法由来已久,最早提出是为了解决 Heatmap 方法 argmax 操作不可微分的问题,通过对网络输出的 Heatmap 计算 Softmax 后求期望的形式得到坐标值。
由于 Integral Pose Regression 方法是基于坐标值进行监督,因此我选择在 deeppose 方法 head 上进行修改,在 /mmpose/models/heads/ 下复制 deeppose_regression_head.py 创建了一个 integral_pose_regression_head.py,创建 IntegralPoseRegressionHead 类,并在 __init__.py 中进行添加,与此同时我还保留了 RLE 使用的接口。
核心代码大致如下:
@HEADS.register_module()
class IntegralPoseRegressionHead(nn.Module):
def __init__(self,
in_channels,
num_joints,
feat_size,
loss_keypoint=None,
out_sigma=False,
train_cfg=None,
test_cfg=None):
super().__init__()
self.in_channels = in_channels
self.num_joints = num_joints
self.loss = build_loss(loss_keypoint)
self.train_cfg = {} if train_cfg is None else train_cfg
self.test_cfg = {} if test_cfg is None else test_cfg
self.out_sigma = out_sigma
self.conv = build_conv_layer(
dict(type='Conv2d'),
in_channels=in_channels,
out_channels=num_joints,
kernel_size=1,
stride=1,
padding=0)
self.size = feat_size
self.wx = torch.arange(0.0, 1.0 * self.size, 1).view([1, self.size]).repeat([self.size, 1]) / self.size
self.wy = torch.arange(0.0, 1.0 * self.size, 1).view([self.size, 1]).repeat([1, self.size]) / self.size
self.wx = nn.Parameter(self.wx, requires_grad=False)
self.wy = nn.Parameter(self.wy, requires_grad=False)
if out_sigma:
self.gap = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(self.in_channels, self.num_joints * 2)
def forward(self, x):
"""Forward function."""
if isinstance(x, (list, tuple)):
assert len(x) == 1, ('DeepPoseRegressionHead only supports '
'single-level feature.')
x = x[0]
featmap = self.conv(x)
s = list(featmap.size())
featmap = featmap.view([s[0], s[1], s[2] * s[3]])
featmap = F.softmax(featmap, dim=2)
featmap = featmap.view([s[0], s[1], s[2], s[3]])
scoremap_x = featmap.mul(self.wx)
scoremap_x = scoremap_x.view([s[0], s[1], s[2] * s[3]])
soft_argmax_x = torch.sum(scoremap_x, dim=2, keepdim=True)
scoremap_y = featmap.mul(self.wy)
scoremap_y = scoremap_y.view([s[0], s[1], s[2] * s[3]])
soft_argmax_y = torch.sum(scoremap_y, dim=2, keepdim=True)
output = torch.cat([soft_argmax_x, soft_argmax_y], dim=-1)
if self.out_sigma:
x = self.gap(x).reshape(x.size(0), -1)
pred_sigma = self.fc(x)
pred_sigma = pred_sigma.reshape(pred_sigma.size(0), self.num_joints, 2)
output = torch.cat([output, pred_sigma], dim=-1)
return output Integral Pose Regression 方法由于是在 backbone 输出的 8x8 特征图上进行的 Soft-Argmax 操作,因此对推理速度的影响很小,跟纯 Regression 方案基本一致(甚至快了 0.4ms):
elapse 6.5000 ms
elapse 6.3852 ms
elapse 6.3100 ms
elapse 6.3400 ms
elapse 6.5300 ms
3.3 DSNT:为 IPR 分布添加正则约束
最原始的 Integral Pose Regression 方法,即 Soft-Argmax,在这里性能上并没有明显的优势,但却给了我们加入更多监督信息的机会。
相比于 deeppose 直接回归出坐标值,我们可以在 IPR 的分布表征上对分布进行监督,这也就是 2018 年提出的 DSNT 方法,我实现了一个 DSNTLoss,即在 Loss 中加入了对分布的正则化约束。
方便起见,我直接用了 DSNT 论文作者开源的 dsntnn 库中提供的 js_reg_losses,小伙伴们可以通过 pip install dsntnn 获取。
不过 dsntnn 库中的坐标归一化是 [-0.5, 0.5],而 MMPose 使用的是 [0, 1],需要手动修改一下 dsntnn 库中的 normalized_linspace 方法:
# dsntnn/__init__.py:
def normalized_linspace(length, dtype=None, device=None):
"""Generate a vector with values ranging from -1 to 1.
Note that the values correspond to the "centre" of each cell, so
-1 and 1 are always conceptually outside the bounds of the vector.
For example, if length = 4, the following vector is generated:
```text
[ -0.75, -0.25, 0.25, 0.75 ]
^ ^ ^
-1 0 1
```
Args:
length: The length of the vector
Returns:
The generated vector
"""
if isinstance(length, torch.Tensor):
length = length.to(device, dtype)
# first = -(length - 1.0) / length
# return torch.arange(length, dtype=dtype, device=device) * (2.0 / length) + first
return torch.arange(0.0, length, 1, dtype=dtype, device=device) / length
@LOSSES.register_module()
class RLE_DSNTLoss(nn.Module):
"""RLE_DSNTLoss loss.
"""
def __init__(self,
use_target_weight=False,
size_average=True,
residual=True,
q_dis='laplace',
sigma=2.0):
super().__init__()
self.dsnt_loss = DSNTLoss(sigma=sigma, use_target_weight=use_target_weight)
self.rle_loss = RLELoss(use_target_weight=use_target_weight,
size_average=size_average,
residual=residual,
q_dis=q_dis)
self.use_target_weight = use_target_weight
def forward(self, output, heatmap, target, target_weight=None):
assert target_weight is not None
loss1 = self.dsnt_loss(heatmap, target, target_weight)
loss2 = self.rle_loss(output, target, target_weight)
loss = loss1 + loss2 # 这里权重可以调参
return loss
加入 DSNT 后,我们的模型开始有了可以调参的地方(调参侠狂喜),这里有两个:一是渲染的高斯分布方差 sigma 取值,二是 DSNT 跟 RLE 相加的 loss 权重。
另外此处模型需要同时优化两个 loss,而目前 MMPose 只支持单个 loss 的优化,所以写成这样,经过跟 yining 大佬沟通,预计在下半年 MMPose 会加入对多 loss 的支持,并且会采用更优雅的方式实现。
3.4 实验小结二
从结果可以看到:单独使用 integral pose regression 方法相较于 deeppose,能在推理速度不变的情况下带来性能提升。但这还远远不是 IPR 方法的全部实力,IPR 优秀的表征能力配合 RLE 提供的更优质的监督信息,让 regression-based 方法训练效率大大提升,训练 10 个 epoch 的 acc_pose 达到0.70,媲美 Heatmap:
而这里我需要指出的是,IPR 的梯度形式相比于 Heatmap 监督仍然是更差的,这里的暂时追平是 RLE 和 pretrained 共同作用的结果,在后续的训练中 IPR 由于分布形状不明确、梯度不稳定等因素,收敛速度会有一个明显的停滞,从结果也可以看到:除了初期收敛快以外,最终的性能并不比加了 RLE 的 deeppose 高多少(PCKh 上 0.19 个点)。
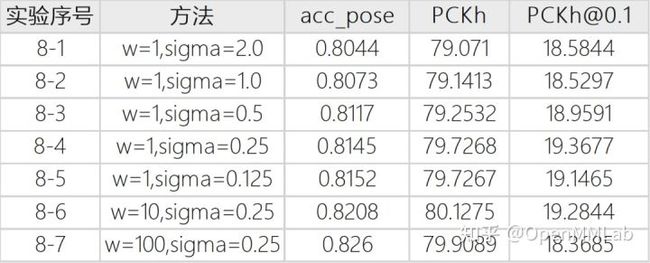
DSNT 的调参方面:
一开始设置的最常用的 sigma=1.0 和 2.0 都有不同程度的掉点,sampling-argmax 论文中也提到:这种强行加约束的方式有时是会导致掉点的,毕竟你很难知道当前的分布尺度最适合的 sigma 是多少。而 DSNT 论文实验这张图也显示,特征图分辨率 7x7 时加约束反而是不如无约束的:
但是后来我考虑到人体姿态估计常用的 Heatmap 尺寸是 64x64,最佳 sigma=2,DSNT 中用的 28x28 可以近似看成 32x32,最佳 sigma=1,那么 8x8 下适用的 sigma 应该等比例缩小到 0.25 或者 0.125,跑了一下实验果然在 0.25 和 0.125 上有了涨点。
再对 DSNT 的正则化 loss 权重进行了简单的调参,最终相较于纯 IPR 有 PCKh 上 0.6 个点的提升。 w=100 时虽然训练阶段 pose_acc 上升了,但 val 的 PCKh 和 PCKh@0.1 都掉点了,这说明出现了过拟合,因此最终我选定 w=10,sigma=0.25 这组参数。
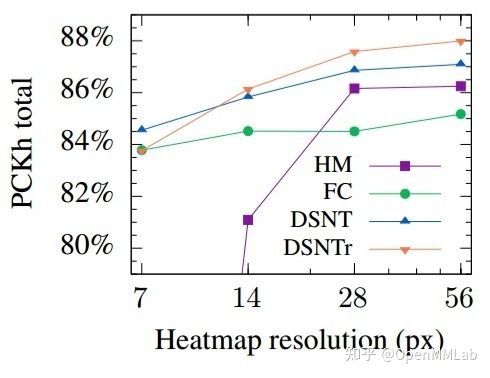
由于我本人不是一个调参爱好者,比起调参还是更倾向于从原理上优化,而且用自己的本地机器调参实在太慢也太蠢了(电费顶不住了),这里就不继续了,从 DSNT 的论文来看,特征图分辨率从 7x7 提升到 28x28 有接近 3 个点的提升,这给我们指明了新道路:增大特征图分辨率。
4. 特征分辨率 & 表征形式
4.1 增大特征图分辨率
特征分辨率对于视觉下游任务的重要性,从 HRNet 之后几乎也是一个共识了,所以这个思路并不难想到。
如果将模型输出的 Heatmap 看成一个二维的离散概率分布,那么这个 Heatmap 的分辨率无疑是与精度高度相关的。
如 DSNT 实验中,把分辨率从 7x7 提升到 28x28 就能有 3 个点的提升(resnet 上),那么在推理速度可以接受的范围内,这无疑是一种提升性能的有效手段。
我效仿 SimpleBaseline 在骨干网络输出的特征图后面接了转置卷积层用于上采样,在我原本代码的基础上只需要把 self.conv 改成堆叠的转置卷积即可。
考虑到推理速度,我没有像 SimpleBaseline 那样用三层通道数为 256 的 deconv,后接一个 1x1 卷积把通道数合并到关键点个数。而是只用了两层 deconv,第一层 256 通道,第二层直接压缩到关键点个数。
SimpleBaseline:
deconv = [256, 256, 256]
conv = Conv2d(256, 16, k=1)
我的做法:
deconv = [256, 16] 这里关于计算量和性能的 trade-off 非常主观,没有太多依据可言,我的做法并不是最优的。
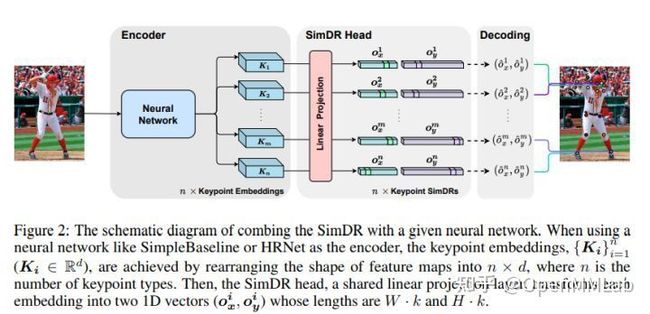
4.2 SimDR
SimDR 论文中的实验证明:关键点表征并不需要全程维护二维的 Heatmap,用一维来表征也是足够的。
这个其实很好理解,毕竟 IPR 方法最后也是分别对 Heatmap 在 x 和 y 轴方向求和得到各自的一维表征,既然这都行得通,那么模型直接预测一维向量表征是相当符合直觉的。
SimDR 论文实验结果显示,使用原图两倍长度以上的一维向量就能取得不亚于二维 Heatmap 的精度:
另外我觉得这个结果可以用香农采样定理来解释,至少要用 2 倍的表征长度(采样频率),才能无损地恢复原尺寸的离散分布。当然,这只是我开的一个脑洞,并不严谨。
遵循 SimDR 的做法,将经过两次上采样得到 32x32 的特征图拉直得到长度为 1024 的一维特征,对这个特征进行线性映射到我们想要的任意长度,然后平均拆分成两段,作为 x 和 y 坐标的特征。
跟论文不同之处在于:原文是按照 Heatmap 方法进行后处理,即对一维特征进行 argmax 获取坐标,而我是用 IPR 的方式用 Soft-Argmax 进行解码,从而保持端到端的训练。
为了验证方法的有效性,对比实验是免不了的,首先实验简单提升分辨率后用 32x32 的 Heatmap 表征的 DSNT 方法精度,后续做法跟上面一样,对 Heatmap 做 Softmax 归一化然后求期望,最终模型的推理速度为:
32x32
elapse 11.2500 ms
elapse 11.0500 ms
elapse 10.9400 ms
elapse 11.0478 ms
elapse 11.6800 ms 使用 SimDR 则是对两个 512 长度的一维特征分别进行 Softmax 归一化,后续做法跟 DSNT 类似,只不过 DSNT 监督的高斯分布是二维 Heatmap,而 SimDR 是在一维上监督,因此 loss 和 target 实现上有区别,但背后的原理是一样的。SimDR 的推理速度为:
simdr 512
elapse 11.8700 ms
elapse 11.7100 ms
elapse 12.0405 ms
elapse 11.9200 ms
elapse 11.9900 ms 原始版本的 SimDR 是使用 one-hot 作为 target,用交叉熵进行监督的,这样的做法是完全将定位问题当成分类问题来处理,这样做虽然可以,但还有提升的空间,即像 Heatmap 方法一样用高斯分布作为 target,用 KL 散度来监督。采用了高斯分布监督的 SimDR 方法在论文中称为 SA-SimDR,论文实验中 SA-SimDR 在 COCO 上性能超过了 Heatmap 方法。
4.3 实验小结三
单纯的 SimDR 如果不加高斯分布监督,取得的结果跟加了 DSNT 的大分辨率结果比掉了大概 0.3 个点。
这里就又涉及到需要调参,sigma 的选择,由于当前的一维表征长度为 512,我按照之前的经验先取到 sigma=4,PCKh 有 0.3 个点的提升,基本追平了之前的 DSNT 方法。
随后我查阅了 SimDR 源代码发现作者使用的是 sigma=6,实验后取得了 82.115 的 PCKh,此时已经超越了 DSNT 方法。
由于我一开始选用的上采样策略非常激进,后面我在 deconv 后补了一个 1x1 卷积。可以看到这层 1x1 卷积能带来 0.2 个点的提升。
5. 公式调参 & Dropout
实验进行到这里,似乎能调的参数都已经调的差不多了,但是我们的模型距离 Heatmap 方法还有 2.5 个点的差距,怎么办呢?在这里我分享一点调参侠独门秘籍,从已有的方法原理里找可以调的参数。
5.1 Softmax
首先是 Softmax 这个函数,大家应该都不陌生,完整的公式为:
L=ezy/τ∑i=1Cezi/τ
这里的 smooth 系数 τ 常常被省略,但实际上它是一个调整 Softmax 平滑程度的系数。当输入的响应值过小时,Softmax 的结果往往过于平滑,这会导致 Soft-Argmax 的结果趋近于分布的中央,不能正确地得到最大值位置,所以就需要通过 τ 来增大输入值,使得 Softmax 的输入保持在一个合适的精度范围。
但事实上,增大 smooth 系数来提升 Softmax 近似程度并不好,这会导致梯度消失,后来我读到了王峰大佬的博文《Softmax 理解之 Smooth 程度控制》,里面给出了一个更合理的优化方案:
在人脸识别任务中,网络的最后一层线性变换分类层,实际上可以看成是把前一层输出的特征,与最后一层的权重在计算内积。如果把特征和权重都进行归一化,那么最后一层的物理含义就变成了计算余弦相似度,取值范围就限定在了 [-1, 1],所以特征图的响应值范围就限定下来了,接下来再乘上一个尺度因子 s 来拉大响应幅度,就可以很容易地保证输入到 Softmax 里的分数能在一个合适的范围:
L=eszy~∑i=1Ceszi~
如此一来,就能使得网络的响应值始终控制在 Softmax 拟合程度好的范围,减小 Softmax 自身性质引入的计算误差。
而实现这一点也很简单,只需要增加两个全连接层:
feat_x, feat_y = torch.chunk(pred_simdr, 2, dim=-1)
mlp_x_norm = torch.norm(self.mlp_x.weight, dim=-1)
norm_x = torch.norm(feat_x, dim=-1, keepdim=True)
feat_x = self.mlp_x(feat_x)
feat_x /= norm_x
feat_x /= mlp_x_norm.reshape(1, 1, -1)
feat_x *= self.beta
mlp_y_norm = torch.norm(self.mlp_y.weight, dim=-1)
norm_y = torch.norm(feat_y, dim=-1, keepdim=True)
feat_y = self.mlp_y(feat_y)
feat_y /= norm_y
feat_y /= mlp_y_norm.reshape(1, 1, -1)
feat_y *= self.beta 此处的 beta 作为缩放系数,是可以进行调参的,由于过大的 beta 会导致梯度消失,我写了一个简单的脚本来估计合适的缩放范围:
def soft_argmax(idx, value, length):
size = length
# 定义一个一维的长度为10的分布
a = torch.zeros((size, ))
# 在第8项上设置响应
target_idx = idx
a[target_idx] = value
# print('dist:\n', a)
# 进行softmax归一化
softmax_res = a.softmax(0)
# print('after softmax:\n', softmax_res)
# 求期望值
lin = torch.tensor([x for x in range(size)])
expectation = (lin * softmax_res).sum()
# print('expectation:\n', expectation)
return expectation
for x in [1, 10, 11,12,13,14,15,16, 20, 30,32, 40, 50, 100, 256, 512]:
length = 512
err = 0.
for idx in range(length):
expect = soft_argmax(idx, x, length)
err += (idx - expect)**2
print(x, err)
1 tensor(11110072.)
10 tensor(5772.4692)
11 tensor(804.1144)
12 tensor(110.0054)
13 tensor(14.9522)
14 tensor(2.0244)
15 tensor(0.2741)
16 tensor(0.0369)
20 tensor(1.3588e-05)
30 tensor(1.4985e-16)
32 tensor(2.7446e-18)
40 tensor(3.0886e-25)
50 tensor(6.3661e-34)
100 tensor(0.)
256 tensor(0.)
512 tensor(0.) 这个脚本统计了不同长度的表征时,不同响应值带来的误差,取到 15 左右时 Soft-Argmax 的误差在 1 以内,因此我选择了 15 作为 beta。按理来说随着模型训练进行,beta 可以逐渐增大来使得预测更加准确,但我没有进行尝试了。
5.2 RLE
关于 RLE 其实有一个不太多人知道的小趣事,indigo 和 yining 大佬在向 MMPose 添加 RLE 方法的过程中,发现作者开源的 RLE 代码跟论文公式有一点小出入,logQ 中多加了一个 log(sigma)。
RLE 公式如下:
代码实现:
if self.q_dis == 'laplace':
loss_q = torch.log(sigma * 2) + torch.abs(error)
else:
loss_q = torch.log(sigma * math.sqrt(2 * math.pi)) + 0.5 * error**2 这一项的引入可能是由于疏忽,因为按照原文的定义,Q 应该是一个标准分布,因此 sigma 为 1,跟模型预测的 out_sigma 是不同的。但是在去掉这个 log(sigma) 后模型出现了掉点,因此大家最终决定保留了这一项。
那么这多出来的 log(sigma) 为什么会起作用呢?
我个人目前觉得可以从多任务学习的角度来理解,多出来的这一项可以看成一个 aux_loss,让模型在优化 RLE 的同时,也需要优化另一个辅助任务,而这个辅助任务的目标是尽量缩小 sigma。
在 RLE 方法中,模型预测的 sigma 是完全自适应优化的,用来反映模型预测的不确定度,尽管损失函数本身就会倾向于让 sigma 缩小,但既然增加这一项能涨点,这就说明模型原本对 sigma 缩小这个目标的权重还不够。
在 RLE 论文中,作者提出可以用 sigma 来计算预测的置信度:
c^=1−1K∑iKσi^
于是我输出了随着训练进行用 sigma 预测关键点存在性的准确率,结果是默认情况下随着训练的进行,sigma 预测的准确率在降低,这说明自适应优化的 sigma 并没有很好地减小,甚至反而在增大。
所以到了这里,我们就可以很自然地给这多出来的 log(sigma) 加上一个权重进行调参了(调参侠再次狂喜):
if self.q_dis == 'laplace':
loss_q = gamma * torch.log(sigma * 2) + torch.abs(error)
else:
loss_q = gamma * torch.log(sigma * math.sqrt(2 * math.pi)) + 0.5 * error**2 增大了 log(sigma) 权重后,sigma 预测的准确率停止了下降,不过出现一个现象:权重不论取多大,每一轮的准确率变化都一模一样:
我推测这个现象出现的原因是加大权重后,使得模型倾向于一直缩小 sigma,因此把所有点都预测为存在了,毕竟目前没有监督信息。
这里的调参我小偷了一下懒,没有再跑满 210 epoch,而是根据 10 个 epoch 后的 PCKh 来选择(电费真顶不住了)。
5.3 GFLv1v2
既然观察到了 sigma 变化趋势,很自然地会想到给 sigma 加一个监督,就用 target_weight 信息即可,因为当关键点存在时我们会希望 sigma 小,反之希望 sigma 越大越好。
这里我先实验了最简单的 binary crossentropy,随后将 bce loss 换成了 GFLv1 中提出的 Quality Focal Loss,最后再添加了 GFLv2 中提出的轻量头部,用坐标表征的统计值学习一个权重,乘到 sigma 预测的分支上。
5.4 Dropout
在前面的实验中我们可以发现:大量全连接层的应用已经使得模型出现了比较严重的过拟合,验证集上 82 的时候训练集指标已经 89 了,因此引入一些正则化手段是有必要的,这里我用了 Dropout,这是我们刚开始接触深度学习几乎都会学到的一个技术。
5.5 实验小结四
从结果来看:
- 基于 Softmax 的优化对于 PCKh@0.1 的提升比较明显
- 为 log(sigma) 加权主要是提升了模型初期的收敛速度,且使模型训练更加稳定,但对最终提点没有太大的帮助
- 对 sigma 加监督信息后可以提升存在性预测的准确率,但是会干扰定位任务的学习
- 加 Dropout 能有效减轻过拟合,并能带来 0.2 个点的提升
- 采用 QFL 比 BCE 对存在性预测的效果更好,但也更加影响定位任务的学习
- DGQP 可以进一步强化 QFL 的效果,但对定位任务的影响更加严重,也许可以通过加长训练周期来解决
目前模型的推理速度为 11.7ms:
elapse 12.0525 ms
elapse 12.0392 ms
elapse 11.7625 ms
elapse 11.4900 ms
elapse 11.7952 ms 6. 图片分辨率 & 抑制过拟合
6.1 增大图片分辨率
提升输入图片的分辨率同样是一个常见的手段了,但我选择放到最后来使用,因为这种方式增加的计算量是巨大的,很容易挤占别的方法的优化空间。得益于我前面的“勤俭节约”,目前模型还有一些算力空间可以给我挥霍,我选择了在这里祭出这个万金油操作。
由于图片分辨率增加带来的计算量提升是影响整个模型的,我实验了输入 320x320,推理时间为:
elapse 17.9134 ms
elapse 17.7805 ms
elapse 17.6927 ms
elapse 17.4205 ms
elapse 17.4552 ms 结果如下:
6.2 抑制过拟合
到了这一步,我们一开始的精度目标已经达成了,Regression 方法用 17ms 的推理速度达到了比 Heatmap 更高的精度,但是前面我也提到,在本地测试一般我会以 15ms 作为接受的底线,于是需要考虑如何在不尽量损失精度的情况下把速度优化下来。
首先我减去了一层 deconv 层,只留下一层 deconv 进行上采样后接 1x1conv。
受到上一节 Dropout 的启发,我们知道现在的模型其实是存在比较严重的过拟合现象的,即使加入了 Dropout 层,训练集和验证集上的指标依然存在 4 个点的差距,所以我继续从降低过拟合的角度来入手。
降低过拟合最直接的方式当然是减少参数量,但我们本来就是轻量模型,参数每减一点都可能对性能有很大影响,所以如何减参数是需要谨慎考虑的。至于其他的正则化手段,不论是 weight_decay 还是增大 Dropout 比例,我实验后无一例外也都掉点了。
最终我在分析可能导致过拟合的模块时,把目光集中到了 shufflenetv2 的最后一层上,作为一个为分类模型设计的 backbone,在分类问题上提点的一个有效手段是:在输出的最后一层对特征进行升维。
以 shufflenetv2 x1.0 为例,模型最后一个 stage 输出的特征维度本身应该是 464 维的,但是最后用一个 1x1 卷积升到了 1024 维,如果是做分类问题的话,后面会接 GAP层然后全连接层,目的是升高维度有利于多类别之间的特征学习,让特征在高维空间更容易区分开,但对于我们的关键点定位任务,其实并不需要这么高的特征维度。
考虑到 RLE 用来预测 sigma 的流程跟分类问题比较相似(GAP+FC),最终我选择了让 backbone 输出两张特征图,1024 维的特征用来预测 sigma,464 维的特征送去做定位,最终推理速度为:
elapse 12.2600 ms
elapse 12.4100 ms
elapse 12.2900 ms
elapse 12.3300 ms
elapse 12.4200 ms
6.3 实验小结五
最终的实验效果如下:
可以看到过拟合现象被进一步缓解,在接近 5ms 的速度提升的同时精度几乎没有降低,至此,我们以 12.3ms 的推理速度让基于 Regression 方法的模型,达到了超越 Heatmap 方法的精度,且推理速度快了近 3 倍。
7. 不讲武德系列
代码框架和模型搭好以后,由于我所有的优化都是与backbone无关的,可以随意替换更强的 backbone,恰好最近 mt-yolov6 开源,我也紧跟时事随手测了一波。
yolov6-n
elapse 14.6300 ms
elapse 14.8100 ms
elapse 14.6400 ms
elapse 14.6800 ms
elapse 14.7100 ms yolov6-n 模型的 backbone 加到本模型上推理速度大概 14.7ms,参数量比 shufflenetv2 多了接近 4MiB,最终性能提升了 1 个点:
由于是用的一样的训练配置,可以看到训练集上指标还低于验证集,所以按理来说还有很大的调参空间,性能应该还能再继续提升一波。这个提升其实也不意外,对 backbone 加重参数技巧带来提点也是目前业务上必加的技巧了,由于本文的目的不在于改进 backbone,而且 backbone 替换带来的涨点,跟原先基于 shufflenetv2 的 Heatmap 方法精度进行对比也不公平,所以这里只是稍微展示一下效果。
8. 一些没有起到作用的技术
8.1 Debiased IPR
在 ICCV 2021 中有一篇工作通过数学方法对 Softmax 引入的误差进行了修正,论文中取得了不错的效果,但是我自己根据论文理解实现的版本效果并不理想,我已向作者发邮件进行了联系,希望能得到作者的帮助。
8.2 Sampling-Argmax
Sampling-Argmax 是 RLE 作者在 NeuraIPS 2021 的工作,核心思想是对 IPR 的改进,针对 IPR 梯度不稳定的问题,设计了一个用重参数技巧来解决的方案,能提供更加稳定的梯度。
在我的实验中,该方法的确可以正常训练,但是最终取得的效果并没有直接用高斯分布监督的精度高。
无法复制加载中的内容
8.3 TokenPose
TokenPose 也是 Transformer 火了之后很自然的一篇工作,原文的主旨是将 Transformer Decoder 作为 Head 来预测 Heatmap,在本项目中我们也可以很自然地用来预测 SimDR 表征,在这里我实验了两种方案,第一种是直接用 TokenPose 替换 deconv 层,即 backbone 提取出来的特征直接送给 TokenPose,这样的好处是可以节省计算量,坏处是转换比较激进,直觉上感觉性能可能会不如 deconv 后的效果,所以又实验了第二种方案,先 deconv 后再进行 TokenPose。
不过考虑到延迟问题,响应的超参数肯定也需要做调整。这里第一种使用的 patch size 为 2x2,第二种则需要改为 8x8,即使如此第二种的推理速度也还是慢了不少。
直接输入
elapse 10.7900 ms
elapse 10.9153 ms
elapse 10.6500 ms
elapse 10.8200 ms
elapse 10.8300 ms
deconv版本 4层transformer
elapse 18.7656 ms
elapse 17.6152 ms
elapse 18.2700 ms
elapse 17.9800 ms
elapse 17.8400 ms
deconv版本 3层transformer
elapse 16.9900 ms
elapse 16.8600 ms
elapse 16.9600 ms
elapse 16.8800 ms
elapse 17.3652 ms
另外我注意到加了 tokenpose 后训练初期的效果差了很多,毕竟基于卷积得到的预训练特征对于 mlp 众多的 transformer 而言确实效果有限。
{"mode": "train", "epoch": 1, "iter": 100, "lr": 0.0001, "memory": 3678, "data_time": 0.07201, "reg_loss": 26.4141, "acc_pose": 0.07084, "loss": 26.4141, "time": 1.00655}
{"mode": "train", "epoch": 2, "iter": 100, "lr": 0.00027, "memory": 3678, "data_time": 0.0604, "reg_loss": -33.63047, "acc_pose": 0.19622, "loss": -33.63047, "time": 0.96591}
{"mode": "train", "epoch": 3, "iter": 100, "lr": 0.00045, "memory": 3678, "data_time": 0.06313, "reg_loss": -47.45935, "acc_pose": 0.24253, "loss": -47.45935, "time": 0.92242}
{"mode": "train", "epoch": 4, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.06104, "reg_loss": -62.17723, "acc_pose": 0.39696, "loss": -62.17723, "time": 0.91032}
{"mode": "train", "epoch": 5, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.06199, "reg_loss": -72.71697, "acc_pose": 0.49004, "loss": -72.71697, "time": 0.95145}
{"mode": "train", "epoch": 6, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.05916, "reg_loss": -76.37753, "acc_pose": 0.51472, "loss": -76.37753, "time": 0.96653}
{"mode": "train", "epoch": 7, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.063, "reg_loss": -78.6295, "acc_pose": 0.53032, "loss": -78.6295, "time": 0.9599}
{"mode": "train", "epoch": 8, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.05949, "reg_loss": -79.18694, "acc_pose": 0.53346, "loss": -79.18694, "time": 1.02493}
{"mode": "train", "epoch": 9, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.06176, "reg_loss": -82.34116, "acc_pose": 0.55703, "loss": -82.34116, "time": 1.03079}
{"mode": "train", "epoch": 10, "iter": 100, "lr": 0.0005, "memory": 3678, "data_time": 0.06209, "reg_loss": -83.11978, "acc_pose": 0.56071, "loss": -83.11978, "time": 0.95358}
实验效果方面,加了 tokenpose 后模型其实并没有涨点,反倒是掉了 0.3 个点,在 mpii 这种小数据集上要从头训 transformer 还是有点太勉强了。根据我过去的个人经验,如果数据量能达到百万级别,加 transformer 是可以带来性能提升的。
9. 结语
在本文中,我围绕算法对一个经典的轻量姿态估计模型进行了优化,最终以 CPU 下单线程推理 12ms 的速度取得了超越 Heatmap 方法的精度,以及接近 3 倍的速度提升。而在实际项目中,其实还会在backbone、数据处理、部署代码等方面进行优化,推理速度和精度还有进一步大幅提升的空间,如果有机会我还会继续总结成文章分享出来。
对我个人而言,这个过程让我对 MMPose 的掌握加深了很多,以后可以轻松基于 MMPose 复现各种新的方法,也方便我今后对新的技术进行横向对比,这是我最大的收获。
最后,如果觉得我写的东西对你有所帮助,希望能点赞鼓励一下,感谢支持~
欢迎大家体验 MMPose,也欢迎社区的小伙伴给我们投稿呀~
https://github.com/open-mmlab/mmposegithub.com/open-mmlab/mmpose