POJ 1085 Triangle War 博弈 （对抗搜索 alpha-beta 剪枝）

Triangle War

Description
Triangle War is a two-player game played on the following triangular grid:
Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important.

For example, if A fills in the line between 2 and 5 in the partial game on the left below:

Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A’s turn again.
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.

Input
You will be given a number of games in the input. The first line of input is a positive integer indicating the number of games to follow. Each game starts with an integer 6 <= m <= 18 indicating the number of moves that have been made in the game. The next m lines indicate the moves made by the two players in order, each of the form i j (with i < j) indicating that the line between i and j is filled in that move. You may assume that all given moves are legal.

Output
For each game, print the game number and the result on one line as shown below. If A wins, print the sentence “A wins.” If B wins, print “B wins.”

Sample Input
4
6
2 4
4 5
5 9
3 6
2 5
3 5
7
2 4
4 5
5 9
3 6
2 5
3 5
7 8
6
1 2
2 3
1 3
2 4
2 5
4 5
10
1 2
2 5
3 6
5 8
4 7
6 10
2 4
4 5
4 8
7 8

Sample Output
Game 1: B wins.
Game 2: A wins.
Game 3: A wins.
Game 4: B wins.

题意：
游戏有A、B两人参与。A先走，每人每次任选一条虚线填成实线。而如果某人填完一条线段后，该线段与另外两条相邻的实线组成了一个单位三角形，该三角形被标记为该游戏者所有，且该游戏者必须接着再填一条虚线。当18条线段被填充完毕后，拥有三角形多的玩家获胜。
首先输入一个数 T ，表示试验次数；接着一个数 n，表示当前局面已经走了 n 条边；接着输入 n 对数，每对数字表示一条填充边，由 A 开始。问从给出的局面开始，双方都采取最优策略，最终谁会取胜。

思路：
博弈问题， alpha-beta 搜索算法的应用。

#include      
#include     
#include     
#include     
#include 
#define LL long long 
using namespace std;    

//10个顶点之间的连线编号  
int mat[11][11]={  
                {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},    
                {0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0},    
                {0, 0, 0, 2, 3, 4, 0, 0, 0, 0, 0},    
                {0, 1, 2, 0, 0, 5, 6, 0, 0, 0, 0},    
                {0, 0, 3, 0, 0, 7, 0, 9, 10,0, 0},    
                {0, 0, 4, 5, 7, 0, 8, 0, 11,12,0},    
                {0, 0, 0, 6, 0, 8, 0, 0, 0, 13,14},    
                {0, 0, 0, 0, 9, 0, 0, 0, 15,0, 0},    
                {0, 0, 0, 0, 10,11,0, 15,0, 16,0},    
                {0, 0, 0, 0, 0, 12,13,0, 16,0, 17},    
                {0, 0, 0, 0, 0, 0, 14,0, 0, 17,0}    
};    
//9个三角形组成的边状态压缩一下  
int tri[9] = {7, 152, 52, 352, 34304, 3200, 71680, 12544, 155648};    
int end_state = (1 << 18) - 1;  // 终结状态 2^18 - 1 ，即所有边均被填充  

int get_state(int pre_state, int seg, int &cnt){  
    int now_state = pre_state | seg;  // 当前局面并上一条边形成新局面  
    for(int i=0; i<9; i++){
        if((pre_state & tri[i]) != tri[i] && (now_state & tri[i]) == tri[i])  
            cnt++;//之前不包含这个三角形，现在包含了  
    }  
    return now_state;  
}  

int MaxSearch(int state, int alpha, int ca, int cb);

int MinSearch(int state, int beta, int ca, int cb){  
    if(ca >= 5) return 1;  
    if(cb >= 5) return -1;//出现5个三角形，胜负已分 
    if(state == end_state) return ca > cb ? 1 : -1; //所有的边都取了游戏结束  
    int ans = 1;  
    int remain = (~state) & end_state;  //剩下还有哪些边可以取  
    while( remain ){  
        int seg = remain & (-remain);
        int ta = ca, tb = cb;  
        int now_state = get_state(state, seg, tb), val;  
        if(tb > cb) val = MinSearch(now_state, beta, ca, tb);  // 如果得分了，则继续填一条边
        else val = MaxSearch(now_state, ans, ca, tb);// 否则换人填   
        if(val < ans) ans = val; 
        if(val <= beta) return ans;//beta剪枝  
        remain -= seg;  
    }  
    return ans;  
}  

int MaxSearch(int state, int alpha, int ca, int cb){  
    if(ca >= 5) return 1;  
    if(cb >= 5) return -1;  
    if(state == end_state) return ca > cb ? 1 : -1;  
    int ans = -1;  
    int remain = (~state) & end_state;
    while( remain ){  
        int seg = remain & (-remain);
        int ta = ca, tb = cb;  
        int now_state = get_state(state, seg, ta), val;
        if(ta > ca) val = MaxSearch(now_state, alpha, ta, cb);
        else val = MinSearch(now_state, ans, ta, cb); 
        if(val > ans) ans = val; 
        if(val >= alpha) return ans;//alpha剪枝  
        remain -= seg;  
    }  
    return ans;  
}  

int main(){  
    int T, cas = 0; scanf("%d", &T);  
    while( T-- ){  
        int n; scanf("%d", &n); 
        int cnt = 0, state = 0;
        int ca = 0, cb = 0;//两个人分别有几个三角形  
        while( n-- ){  
            int u, v; scanf("%d%d", &u, &v);  
            int ta = ca, tb = cb;  
            state = get_state(state, 1<1) ? cb : ca); //没有新的三角形，  
            if(ta == ca && tb == cb)  
                cnt++;  
        }  
        int ans;  
        if(cnt & 1) ans = MinSearch(state, -1, ca, cb);  
        else ans = MaxSearch(state, 1, ca, cb);  
        printf("Game %d: %c wins.\n", ++cas, ans == 1 ? 'A' : 'B');  
    }  
    return 0;  
}  

转载一篇blog
感觉写的很清晰%%%

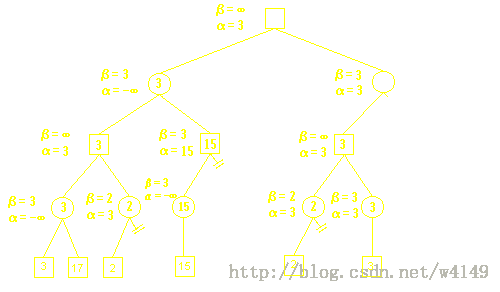
Alpha-Beta剪枝算法(Alpha Beta Pruning)
[说明] 本文基于<>，文中的图片均来源于此笔记。

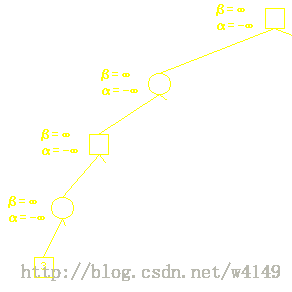
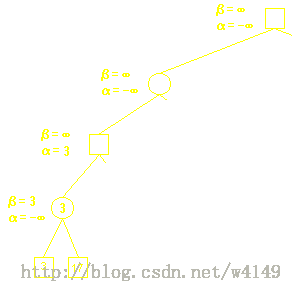
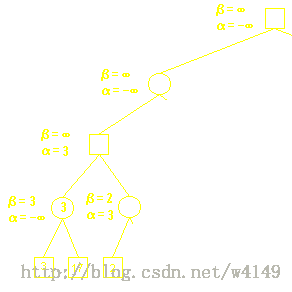
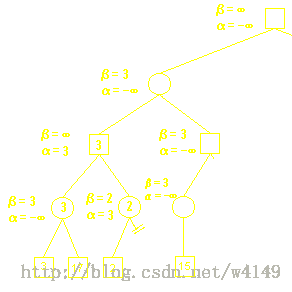
Alpha-Beta剪枝用于裁剪搜索树中没有意义的不需要搜索的树枝，以提高运算速度。

假设α为下界，β为上界，对于α ≤ N ≤ β:
若 α ≤ β 则N有解。
若 α > β 则N无解。

下面通过一个例子来说明Alpha-Beta剪枝算法。 上图为整颗搜索树。这里使用极小极大算法配合Alpha-Beta剪枝算法，正方形为自己（A），圆为对手（B）。 初始设置α为负无穷大，β为正无穷大。 对于B(第四层)而已，尽量使得A获利最小，因此当遇到使得A获利更小的情况，则需要修改β。这里3小于正无穷大，所以β修改为3。 (第四层)这里17大于3，不用修改β。 对于A(第三层)而言，自己获利越大越好，因此遇到利益值大于α的时候，需要α进行修改，这里3大于负无穷大，所以α修改为3 B(第四层)拥有一个方案使得A获利只有2，α=3, β=2, α > β, 说明A(第三层)只要选择第二个方案, 则B必然可以使得A的获利少于A(第三层)的第一个方案,这样就不再需要考虑B(第四层)的其他候选方案了,因为A(第三层)根本不会选取第二个方案,多考虑也是浪费. B(第二层)要使得A利益最小,则B(第二层)的第二个方案不能使得A的获利大于β, 也就是3. 但是若B(第二层)选择第二个方案, A(第三层)可以选择第一个方案使得A获利为15, α=15, β=3, α > β, 故不需要再考虑A(第三层)的第二个方案, 因为B(第二层)不会选择第二个方案. A(第一层)使自己利益最大,也就是A(第一层)的第二个方案不能差于第一个方案, 但是A(第三层)的一个方案会导致利益为2, 小于3, 所以A(第三层)不会选择第一个方案, 因此B(第四层)也不用考虑第二个方案. 当A(第三层)考虑第二个方案时,发现获得利益为3,和A(第一层)使用第一个方案利益一样.如果根据上面的分析A(第一层)优先选择了第一个方案,那么B不再需要考虑第二种方案,如果A(第一层)还想进一步评估两个方案的优劣的话, B(第二层)则还需要考虑第二个方案,若B(第二层)的第二个方案使得A获利小于3,则A(第一层)只能选择第一个方案,若B(第二层)的第二个方案使得A获利大于3,则A(第一层)还需要根据其他因素来考虑最终选取哪种方案.