【论文阅读】Directed Graph Convolutional Network

论文连接：Directed Graph Convolutional Network

摘要

由于GCN的局限性，本文提出了DGCN（有向 图 卷积 网络），通过一阶和二阶邻居关系的应用，并扩展卷积计算。

介绍

GCN主要存在两个缺点：

1. 仅适用于无向图。对于有向图只能采用对称的领接矩阵，得到半正定的拉普拉斯矩阵，但同时也失去了有向图的唯一结构。例如，对于一个表明文章引用关系的有向图，将其转换为无向图是不太合理的。可以采用RNN和GCN的组合来学习时间图，但其添加了额外组件。
2. 仅考虑1跳结点特征。在大多数的基于光谱的GCN中，每个卷积操作中，只捕获了顶点的一阶信息。而没有直接相连的结点也可能存在某些关系，例如社交网络中，拥有共同兴趣的人，不一定相互联系（直接相连）。尽管能够堆叠多层GCN获得更多信息，但多层网络容易导致过拟合。

本文利用二阶邻近点来对现有方法进行扩展，不仅能够保留有向图的方向特征，也能够扩展图卷积的感受域，从而提取更多的特征。本文主要贡献：

• 提出DGCN，性能优于传统GCNs
• 在有向图上定义一阶和二阶邻近度，能够扩展卷积感受域

定义

定义有向图$G=(V,E)$，顶点集$V=(v_1,v_2,...,v_n)$，边集$E\subset \left\{1,...,n\right\}\times \left\{1,...,n\right\}$，如果顶点$i$到顶点$j$之间存在一条有向边，则有$e=(i,j)$。有向图中$(u,v)\ne (v,u)$且$w_{i,j}\ne w_{j,i}$

一阶边：对于顶点$i,j$，如果存在$(i,j)\in E$，则$(i,j)$为一阶边
二阶边：对于顶点$i,j,k$，如果存在$(i,k)and(j,k)\in E$，则$(i,j)$为二阶边

Feature Smoothness（特征平滑度）：评估获得的信息量大小
$${\lambda }_f=\frac{||{\sum }_{i\in V^{\prime }}({\sum }_{e_{i,j}\in E^{\prime }}(x_i-x_j{)}^2)|{|}_1}{|E^{\prime }|\cdot d}$$
$d$为特征维度

Label Smoothness（标签平滑度）：评估标签信息的有效性。本文认为，当当前结点标签和周围结点标签一致时，则信息有效。
$${\lambda }_l=\frac{{\sum }_{e_{i,j}\in E^{\prime }}\mathrm{I}(v_i\simeq v_j)}{|E^{\prime }|}$$
其中$\mathrm{I}(\cdot )$表示指数函数，$v_i\simeq v_j$代表两个顶点标签相同

DGCN

一阶邻近与二阶邻近

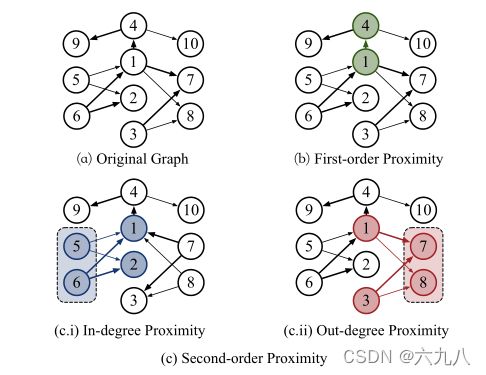
一阶邻近表示直接相连的顶点，如顶点1的一阶邻近包括4、5、6、7、8、9、10
顶点1的二阶邻近为为两种，入度邻近（顶点2）和出度邻近（顶点3），顶点1与顶点2有相同的入度顶点，与顶点3有相同的出度顶点。

First-order Proximity Matrix：
$$A_F(i,j)=A^{sym}(i,j)$$
其中$A^{sym}$为领接矩阵$A$的对称矩阵，相当于将有向图转换为对应的无向图的领接矩阵。
这种转换将导致信息丢失，通过二阶邻近可以将信息保留下来。

Second-order Proximity：
建立一个二阶邻近矩阵，把相似的顶点连接起来：
$$A_{S_{in}}(i,j)=\sum _k\frac{A_{k,i}{A}_{k,j}}{{\sum }_v{A}_{k,v}}$$
$$A_{S_{out}}(i,j)=\sum _k\frac{A_{i,k}{A}_{j,k}}{{\sum }_v{A}_{v,k}}$$
顶点之间的二阶接近度由与其共享邻域节点相连的边的归一化权重总和确定，它能最好地反映顶点vi和vj之间的相似程度，$A_{S_{in}}(i,j)$越大，两个顶点间的二阶相似度越高。
例如上图中：$A_{S_{in}}(1,2)=\frac{A_{1,5}{A}_{2,5}}{2}+\frac{A_{1,6}{A}_{2,6}}{2}=1$

有向图卷积

本文采用一阶和二阶邻近矩阵来实现有向图的卷积。

无向图的卷积公式为：
$$Z^{\prime }=({\widetilde{D^{\prime }}}^{-1/2}\tilde{A}{\widetilde{D^{\prime }}}^{-1/2})X\Theta$$
邻接矩阵$A^{\prime }$存储了图的信息并且给filter提供接受域，从而实现信号$X^{\prime }$到卷积信号$Z^{\prime }$的转换。

同样地，假定有向图的一阶邻近矩阵和二阶邻近矩阵具有相似的功能，一阶矩阵提供’1-hop’的接受域，二阶矩阵提供’2-hop’接受域。
有以下定理：

THEOREM 1. 一阶邻近矩阵和二阶邻近矩阵的拉普拉斯算子是半正定矩阵。

首先，根据一阶邻近与二阶邻近的定义可知，矩阵$A_F,A_{S_{in}},A_{S_{out}}$是对称矩阵。可以将这三个矩阵看作无向图的加权邻接矩阵，根据无向图的卷积可以得到：$$Z_F=f_F(X,{\tilde{A}}_F)=({\widetilde{D_F}}^{-1/2}\widetilde{A_F}{\widetilde{D_F}}^{-1/2})X\Theta$$$$Z_{S_{in}}=f_{S_{in}}(X,{\tilde{A}}_{S_{in}})=({\tilde{D}}_{S_{in}}^{-1/2}{\tilde{A}}_{S_{in}}{\tilde{D}}_{S_{in}}^{-1/2})X\Theta$$$$Z_{S_{out}}=f_{S_{out}}(X,{\tilde{A}}_{S_{out}})=({\tilde{D}}_{S_{out}}^{-1/2}{\tilde{A}}_{S_{out}}{\tilde{D}}_{S_{out}}^{-1/2})X\Theta$$

融合运算

本文基于卷积，又更进一步地采用信息融合的方式，在获取信息的同时保留有向结构。
$$Z=\Gamma (Z_F,Z_{S_{in}},Z_{S_{out}})$$
其中$\Gamma$为融合函数，可以是正则化函数、求和函数、串联操作。本文发现，串联融合的性能最佳，因此有：
$$Z=Concat(Z_F,\alpha Z_{S_{in}},\beta Z_{S_{out}})$$
$Concat(\cdot )$表示矩阵的连接，$\alpha$和$\beta$为权重，反映了不同邻近的重要性。例如，当图的二阶邻居较少时，可以将二阶邻居的权重调小，利用更多的一阶邻居信息进行计算。

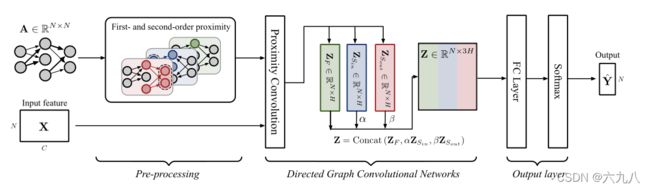
模型

整个模型如上图所示

Pre-processing：提取有向图的一阶和二阶邻近矩阵

Directed Graph Convolutional Networks：根据上述公式进行有向图卷积，将三个邻接矩阵经过同一个滤波器${\Theta }^{(0)}\in R^{C\times H}$，并将三个卷积结果进行Concat，得到一个$N\times 3H$的结果

Output layer：首先将结果输入全连接层，经过一个嵌入-输出的权重矩阵${\Theta }^{(1)}\in R^{3H\times F}$将特征维度转换为$F$。最后通过softmax函数得到预测标签

本文的方法使用一阶和二阶近邻来改善卷积感受野，并且保留了有向信息，具有较强的泛化能力，在大多数基于谱的模型中，都可以利用邻近矩阵来代替原始的邻接矩阵
原始的’k-hop’方法为寻找k层邻居，本文并不是从路径获得信息，而是从顶点的共享属性获取信息

实验

数据集：Cora-Full，Cora-ML，CiteSeer；DBLP（无向图）和PubMed（无向图）。顶点表示文章，边表示引用关系。特征向量为文章的词包

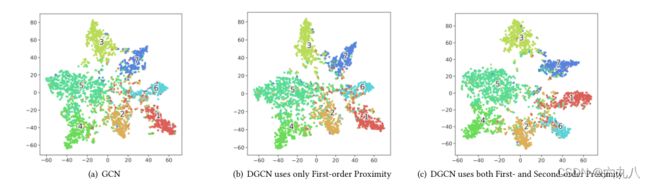
结果展示：

1. 和当前主流的多种模型进行比较，准确率和标准偏差如下表：
   
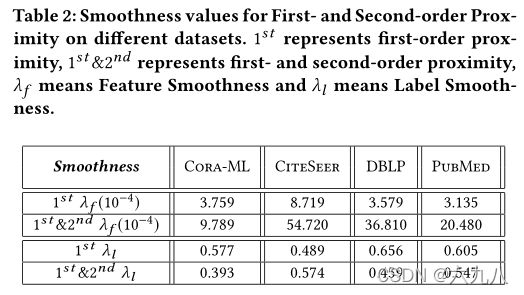
2. 下表展示一阶和一阶二阶结合时的特征平滑度（${\lambda }_f$）和标签平滑度（${\lambda }_l$）。可以看到特征平滑度都有较大幅度的提高，这是由于二阶近似扩大了感受野，从而大大增加了获得的信息量。由于信息量的大幅增加，导致标签平滑度（信息质量）略有下降（可以理解为有大量的噪声）。

3. 可以看到分类的效果更好：

展望

本文的方法能够通过融合一阶和二阶近邻矩阵学习有向图表示。

• 融合函数和连接权重的选择还是手工进行的
• 考虑调整方法，进行小批量训练（mini-batch training）
• 推广到归纳学习