向量自回归与结构向量误差修正模型

 （一）R语言vars包来进行VAR、SVAR和SVECM的建模

  VAR模型

   VAR（y, p=1, type=c("const","trend", "both", "none"), season=NULL， exogen=NULL, lag.max=NULL,ic=c("AIC", "HQ", "SC", "FPE"))

y是一个数据矩阵；p为滞后阶数；type为回归的类型；season为季节数据频数的设置（如果是季节数据，则season=4）；exogen为外生变量矩阵；lag.max为最大滞后阶数；ic为信息准则。

  SVAR模型

    SVAR(x,estmethod=c("scoring", "direct"), Amat=NULL, Bmat=NULL, start=NULL,max.iter=100, conv.crit=1e-07, maxls=1, lrtest=TRUE,...)

x为数据矩阵；estmethod为由得分算法（默认）或负对数似然函数直接最小化估计；Amat和Bmat为A和B的结构系数矩阵；start为未知系数的初始值；conv.crit为收敛值；maxls为最大步长；lrtest为逻辑值，用来确定计算过度识别系统的似然比率。

  SVEC模型

   SVEC(x, LR=NULL, SR=NULL,r=1, start=NULL, max.iter=100, conv.crit=1e-07, maxls=1,lrtest=TRUE, boot=FALSE, runs=100)

x必须为ca.jo类型格式的，也就是说必须由设定协整方程后再构建SVEC；LR和SR分别为设定长期和短期的结构系数矩阵；r为协整方程个数。

  诊断检验

    vars包中进行诊断检验的函数为arch.test(), normality.test(),serial.test()和stability()

  脉冲响应和预测方差误差分解

  脉冲响应函数

   irf(x, impulse=NULL,response=NULL, n.ahead=10, ortho=TRUE, cumulative=FALSE, boot=TRUE,ci=0.95, runs=100,seed=NULL, ...)

  方差分解

  fevd(x,n.ahead=10,...)

 （二）案例分析

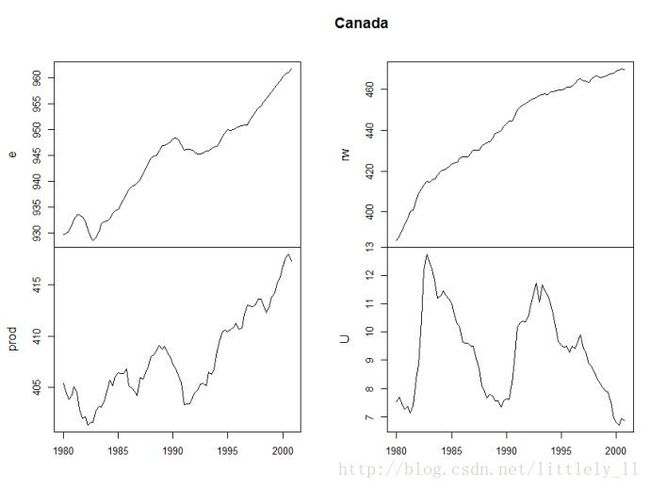
 加拿大的一个宏观经济数据

prod为GDP，e为就业的对数，U为失业率，rw为实际工资水平的对数。

 library(vars)

data(Canada)

summary(Canada)

      e           prod           rw            U       

 Min.  :928.6   Min.  :401.3   Min.  :386.1   Min.  : 6.700  

 1stQu.:935.4   1st Qu.:404.8   1stQu.:423.9   1st Qu.: 7.782 

 Median:946.0   Median :406.5   Median:444.4   Median : 9.450 

 Mean  :944.3   Mean  :407.8   Mean  :440.8   Mean  : 9.321  

 3rdQu.:950.0   3rd Qu.:410.7   3rdQu.:461.1   3rd Qu.:10.607 

 Max.  :961.8   Max.  :418.0   Max.  :470.0   Max.  :12.770  

plot(Canada,nc=2,xlab="")

adf1<-summary(ur.df(Canada[,"prod"],type="trend",lag=2))

adf1

############################################### 

# Augmented Dickey-FullerTest Unit Root Test # 

############################################### 

Test regressiontrend 

Call:

lm(formula = z.diff ~z.lag.1 + 1 + tt + z.diff.lag)

Residuals:

    Min      1Q   Median      3Q    Max 

-2.19924 -0.38994 0.04294  0.41914 1.71660 

Coefficients:

           EstimateStd. Error t value Pr(>|t|)  

(Intercept) 30.415228 15.309403   1.987  0.0506 .

z.lag.1    -0.075791   0.038134 -1.988   0.0505.

tt         0.013896   0.006422  2.164   0.0336*

z.diff.lag1 0.284866   0.114359  2.491   0.0149*

z.diff.lag2 0.080019   0.116090  0.689   0.4927 

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’1

Residual standard error:0.6851 on 76 degrees of freedom

Multiple R-squared: 0.1354, Adjusted R-squared: 0.08993 

F-statistic: 2.976 on 4 and76 DF,  p-value: 0.02438

Value of test-statistic is:-1.9875 2.3 2.3817 

Critical values for teststatistics: 

     1pct  5pct10pct

tau3 -4.04 -3.45-3.15

phi2  6.50 4.88  4.16

phi3  8.73 6.49  5.47

adf2<-summary(ur.df(diff(Canada[,"prod"]),type="drift",lag=1))

adf2

############################################### 

# Augmented Dickey-FullerTest Unit Root Test # 

############################################### 

Test regressiondrift 

Call:

lm(formula = z.diff ~z.lag.1 + 1 + z.diff.lag)

Residuals:

    Min      1Q   Median      3Q    Max 

-2.05124 -0.39530 0.07819  0.41109 1.75129 

Coefficients:

          Estimate Std. Error t valuePr(>|t|)    

(Intercept) 0.11534   0.08029   1.437   0.155   

z.lag.1    -0.68893   0.13350  -5.160 1.83e-06***

z.diff.lag -0.04274   0.11275  -0.379   0.706   

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’1

Residual standard error:0.6971 on 78 degrees of freedom

Multiple R-squared: 0.3615, Adjusted R-squared: 0.3451 

F-statistic: 22.08 on 2 and78 DF,  p-value: 2.526e-08

Value of test-statistic is:-5.1604 13.3184 

Critical values for teststatistics: 

     1pct  5pct10pct

tau2 -3.51 -2.89-2.58

phi1  6.70 4.71  3.86

VARselect(Canada,lag.max=8,type="both")

$selection

AIC(n) HQ(n)  SC(n)FPE(n) 

    3     2     1    3 

$criteria

               1          2          3          4          5          6          7

AIC(n) -6.272579064-6.636669705 -6.771176872 -6.634609210 -6.398132246 -6.307704843-6.070727259

HQ(n) -5.978429449 -6.146420347 -6.084827770-5.752160366 -5.319583658 -5.033056512-4.599979185

SC(n) -5.536558009 -5.409967947 -5.053794411-4.426546046 -3.699388378 -3.118280272-2.390621985

FPE(n) 0.001889842  0.001319462 0.001166019  0.001363175 0.001782055  0.002044202 0.002768551

              8

AIC(n)-6.06159685

HQ(n) -4.39474903

SC(n) -1.89081087

FPE(n) 0.00306012

 

从以上结果可知，AIC和FPE选择3阶之后，SC选择1阶。

Canada<-Canada[,c("prod","e","U","rw")]

p1ct<-VAR(Canada,p=1,type="both")

p1ct

VAR EstimationResults:

======================= 

Estimated coefficients forequation prod: 

========================================= 

Call:

prod = prod.l1 + e.l1 + U.l1+ rw.l1 + const + trend 

   prod.l1       e.l1       U.l1      rw.l1      const     trend 

 0.96313671 0.01291155  0.21108918-0.03909399 16.24340747 0.04613085 

Estimated coefficients forequation e: 

====================================== 

Call:

e = prod.l1 + e.l1 + U.l1 +rw.l1 + const + trend 

     prod.l1        e.l1         U.l1       rw.l1        const       trend 

  0.19465028   1.23892283   0.62301475   -0.06776277-278.76121138  -0.04066045 

Estimated coefficients forequation U: 

====================================== 

Call:

U = prod.l1 + e.l1 + U.l1 +rw.l1 + const + trend 

    prod.l1        e.l1       U.l1       rw.l1       const      trend 

 -0.12319201 -0.24844234   0.39158002  0.06580819 259.98200967  0.03451663 

Estimated coefficients forequation rw: 

======================================= 

Call:

rw = prod.l1 + e.l1 + U.l1 +rw.l1 + const + trend 

    prod.l1        e.l1       U.l1       rw.l1       const      trend 

 -0.22308744 -0.05104397  -0.36863956  0.94890946 163.02453066  0.07142229 

summary(p1ct,equation="e")#选择就业方程

VAR EstimationResults:

========================= 

Endogenous variables: prod,e, U, rw 

Deterministic variables:both 

Sample size:83 

Log Likelihood:-207.525 

Roots of the characteristicpolynomial:

0.9504 0.9504 0.90450.7513

Call:

VAR(y = Canada, p = 1, type= "both")

Estimation results forequation e: 

================================== 

e = prod.l1 + e.l1 + U.l1 +rw.l1 + const + trend 

        Estimate Std. Error t value Pr(>|t|)   

prod.l1   0.19465   0.03612   5.389 7.49e-07***

e.l1      1.23892   0.08632  14.353 < 2e-16 ***

U.l1      0.62301   0.16927   3.681 0.000430***

rw.l1    -0.06776   0.02828  -2.396 0.018991 * 

const  -278.76121   75.18295  -3.7080.000392 ***

trend    -0.04066   0.01970  -2.064 0.042378 * 

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’1

Residual standard error:0.4701 on 77 degrees of freedom

Multiple R-Squared: 0.9975,Adjusted R-squared: 0.9973 

F-statistic: 6088 on 5 and 77 DF,  p-value:< 2.2e-16 

Covariance matrix ofresiduals:

        prod       e       U      rw

prod 0.469517  0.06767 -0.04128 0.002141

e    0.067667  0.22096 -0.13200-0.082793

U   -0.041280 -0.13200  0.12161 0.063738

rw   0.002141 -0.08279  0.06374 0.593174

Correlation matrix ofresiduals:

        prod      e      U       rw

prod 1.000000  0.2101 -0.1728 0.004057

e    0.210085  1.0000 -0.8052-0.228688

U   -0.172753 -0.8052  1.0000 0.237307

rw   0.004057 -0.2287  0.2373 1.000000

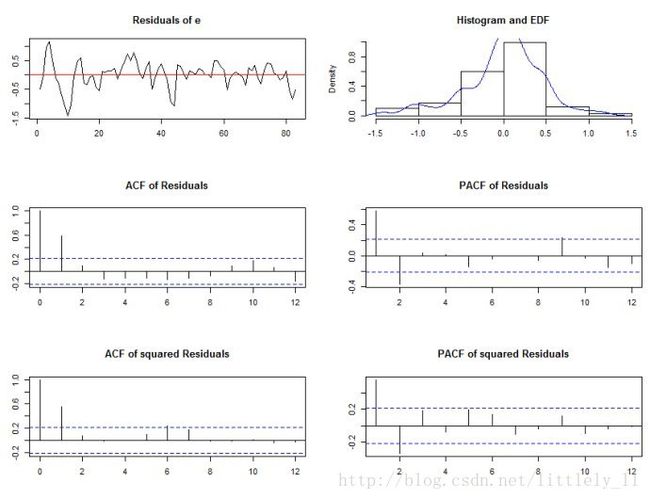
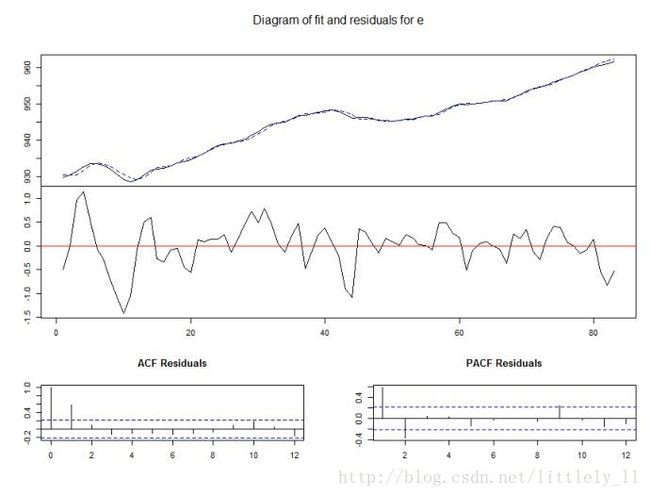
plot(p1ct,names="e")#画出就业对数的拟合、残差图和相关图

 ser11<-serial.test(p1ct,lags.pt=16,type="PT.asymptotic")

ser11$serial

Portmanteau Test(asymptotic)

data: Residuals of VAR object p1ct

Chi-squared = 233.5, df =240, p-value = 0.606

norm1<-normality.test(p1ct)

norm1$jb.mul

$JB

JB-Test(multivariate)

data: Residuals of VAR object p1ct

Chi-squared = 9.9189, df =8, p-value = 0.2708

$Skewness

Skewness only(multivariate)

data: Residuals of VAR object p1ct

Chi-squared = 6.356, df = 4,p-value = 0.1741

$Kurtosis

Kurtosis only(multivariate)

data: Residuals of VAR object p1ct

Chi-squared = 3.5629, df =4, p-value = 0.4684

arch1<-arch.test(p1ct,lags.multi=5)

arch1$arch.mul

ARCH(multivariate)

data: Residuals of VAR object p1ct

Chi-squared = 570.14, df =500, p-value = 0.01606

plot(arch1,names="e")

 plot(stability(p1ct),nc=2)

 

summary(ca.jo(Canada,type="trace",ecdet="trend",K=3,spec="transitory")) #协整检验

###################### 

# Johansen-Procedure# 

###################### 

Test type: trace statistic ,with linear trend incointegration 

Eigenvalues(lambda):

[1] 4.505013e-011.962777e-01 1.676668e-01 4.647108e-022.632104e-17

Values of teststatistic andcritical values of test:

        test 10pct  5pct 1pct

r <= 3 | 3.85 10.49 12.25 16.26

r <= 2 | 18.72 22.7625.32 30.45

r <= 1 | 36.42 39.0642.44 48.45

r = 0  |84.92 59.14 62.99 70.05

Eigenvectors, normalised tofirst column:

(These are the cointegrationrelations)

           prod.l1      e.l1      U.l1     rw.l1   trend.l1

prod.l1  1.00000000  1.0000000  1.0000000 1.0000000  1.0000000

e.l1    -0.02385143  1.2946681-2.8831559  4.2418087 -8.2903941

U.l1     3.16874549 3.4036732 -7.4261514  6.8413561-12.5578436

rw.l1    1.83528156 -0.3330945 1.3978789 -0.1393999  2.4466500

trend.l1 -1.30156097-0.2302803 -0.5093218 -1.5925918  0.2831079

Weights W:

(This is the loadingmatrix)

          prod.l1       e.l1       U.l1       rw.l1     trend.l1

prod.d -0.006535281-0.02763446 -0.070975296 -0.014754352 1.077469e-11

e.d   -0.008503348  0.11414011-0.008156659  0.003988051 7.400296e-12

U.d   -0.004718574 -0.06154306 0.020719431 -0.006557248-4.663893e-12

rw.d  -0.046213350 -0.14579644 -0.016945105  0.011896044 6.952035e-12

summary(ca.jo(Canada,type="trace",ecdet="trend",K=2,spec="transitory"))

###################### 

# Johansen-Procedure# 

###################### 

Test type: trace statistic ,with linear trend incointegration 

Eigenvalues(lambda):

[1] 4.483918e-012.323995e-01 1.313250e-01 4.877895e-029.508809e-17

Values of teststatistic andcritical values of test:

        test 10pct  5pct 1pct

r <= 3 | 4.10 10.49 12.25 16.26

r <= 2 | 15.65 22.7625.32 30.45

r <= 1 | 37.33 39.0642.44 48.45

r = 0  |86.12 59.14 62.99 70.05

Eigenvectors, normalised tofirst column:

(These are the cointegrationrelations)

          prod.l1       e.l1      U.l1     rw.l1  trend.l1

prod.l1  1.0000000   1.0000000  1.00000000 1.000000  1.000000

e.l1     2.7132129 -6.3190324  0.49616472 16.333916-10.368563

U.l1     8.8369211 -15.2682881 1.48062661 25.774259 -16.048489

rw.l1   -0.3716323   3.1817254-0.04085215 -2.546391   4.927457

trend.l1 -0.4177976 -0.9335588 -0.26592659 -3.413555 -1.753060

Weights W:

(This is the loadingmatrix)

          prod.l1       e.l1      U.l1       rw.l1     trend.l1

prod.d 0.023155644 -0.02832697 -0.10914770 -0.006295988-4.784701e-13

e.d    0.005602438 -0.01739149 0.08679396 -0.001019323-4.385546e-13

U.d   -0.019277135  0.01381763-0.03696147 -0.002276871 4.919886e-13

rw.d  -0.084618968 -0.02739056 -0.07798404  0.003985020-1.032315e-13

vecm<-ca.jo(Canada[,c("rw","prod","e","U")],type="trace",ecdet="trend",K=3,spec="transitory")

vecm.r1<-cajorls(vecm,r=1)#VEC模型

vecm.r1

$rlm

Call:

lm(formula =substitute(form1), data = data.mat)

Coefficients:

        rw.d      prod.d     e.d      U.d     

ect1     -0.084815 -0.011994  -0.015606 -0.008660

constant 55.469125   8.274808 10.331308  5.687832

rw.dl1   -0.012082   0.004707 -0.078491  0.017263

prod.dl1 -0.074493   0.234441  0.200953 -0.138916

e.dl1    -0.634084  -0.246544  0.821558 -0.646846

U.dl1     0.063137 -0.979868   0.003379 -0.191125

rw.dl2   -0.157388  -0.190264 -0.095835  0.080354

prod.dl2 -0.251940  -0.029520  0.048273 -0.002909

e.dl2     0.081197 -0.580473  -0.459693 -0.019741

U.dl2    -0.230009  -0.128101 -0.103415 -0.262685

$beta

             ect1

rw.l1    1.00000000

prod.l1  0.54487553

e.l1    -0.01299605

U.l1     1.72657188

trend.l1-0.70918872

vecm<-ca.jo(Canada[,c("prod","e","U","rw")],type="trace",ecdet="trend",K=3,spec="transitory")

SR<-matrix(NA,nr=4,nc=4)#根据经济理论设定短期和长期结构系数矩阵

SR[4,2]<-0

LR<-matrix(NA,nr=4,nc=4)

LR[1,2:4]<-0

LR[2:4,4]<-0

svec<-SVEC(vecm,LR=LR,SR=SR,r=1,lrtest=F,boot=T)#构建SVEC模型

summary(svec)

SVEC EstimationResults:

======================== 

Call:

SVEC(x = vecm, LR = LR, SR =SR, r = 1, lrtest = F, boot = T)

Type:B-model 

Sample size:81 

Log Likelihood:-161.838 

Number of iterations:12 

Estimated contemporaneousimpact matrix:

       prod       e        U    rw

prod 0.58402  0.07434 -0.1525780.06900

e   -0.12029  0.26144 -0.1550960.08978

U    0.02526 -0.26720  0.0054880.04982

rw   0.11170  0.00000 0.483771 0.48791

Estimated standard errorsfor impact matrix:

       prod      e      U    rw

prod 0.09387 0.12013 0.216520.09304

e   0.06461 0.05874 0.16346 0.04542

U   0.05479 0.05526 0.06906 0.03374

rw  0.14126 0.00000 0.65297 0.09234

Estimated long run impactmatrix:

       prod      e      Urw

prod 0.7910  0.0000 0.0000  0

e    0.2024  0.5769 -0.4923 0

U   -0.1592 -0.3409  0.1408 0

rw  -0.1535  0.5961 -0.2495 0

Estimated standard errorsfor long-run matrix:

      prod     e     Urw

prod 0.1435 0.0000 0.0000 0

e   0.2220 0.1976 0.5540 0

U   0.1096 0.1032 0.1435 0

rw   0.17580.1806 0.2544  0

Covariance matrix of reducedform residuals (*100):

       prod     e      U    rw

prod 37.4642 -2.096 -0.2512 2.509

e   -2.0960 11.494 -6.9273 -4.467

U   -0.2512 -6.927  7.4544 2.978

rw   2.5087 -4.467  2.978348.457

LR[3,3]<-0

svec.oi<-update(svec,LR=LR,SR=SR,lrtest=T,boot=F)#模型的优化

svec.oi

SVEC EstimationResults:

======================== 

Estimated contemporaneousimpact matrix:

       prod      e       U     rw

prod 0.58402  0.1199 0.11200 0.07039

e   -0.12029  0.3111 0.04089 0.09159

U    0.02526 -0.2571  0.096740.05083

rw   0.11170  0.0000 -0.473610.49778

Estimated long run impactmatrix:

       prod      e      U rw

prod 0.7910  0.0000 0.000000 0

e    0.2024  0.6768 0.238920 0

U   -0.1592 -0.3688 0.000000 0

rw  -0.1535  0.6456 0.003105 0

summary(svec.oi)

SVEC EstimationResults:

======================== 

Call:

SVEC(x = vecm, LR = LR, SR =SR, r = 1, lrtest = T, boot = F)

Type:B-model 

Sample size:81 

Log Likelihood:-164.876 

Number of iterations:17 

LR overidentificationtest:

LRoveridentification

data: vecm

Chi^2 = 6.1, df = 1, p-value= 0.01

Estimated contemporaneousimpact matrix:

       prod      e       U     rw

prod 0.58402  0.1199 0.11200 0.07039

e   -0.12029  0.3111 0.04089 0.09159

U    0.02526 -0.2571  0.096740.05083

rw   0.11170  0.0000 -0.473610.49778

Estimated long run impactmatrix:

       prod      e      U rw

prod 0.7910  0.0000 0.000000 0

e    0.2024  0.6768 0.238920 0

U   -0.1592 -0.3688 0.000000 0

rw  -0.1535  0.6456 0.003105 0

Covariance matrix of reducedform residuals (*100):

       prod     e      U    rw

prod 37.2953 -2.192 -0.1664 4.723

e   -2.1921 12.132 -7.4408 1.279

U   -0.1664 -7.441  7.8671-1.770

rw   4.7233  1.279 -1.769748.457

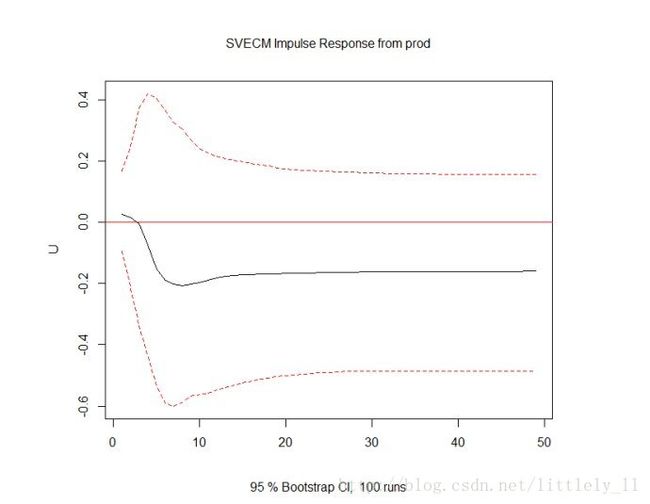
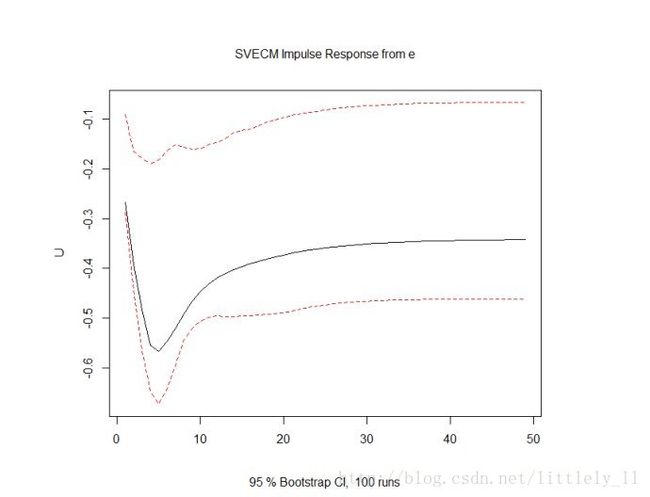
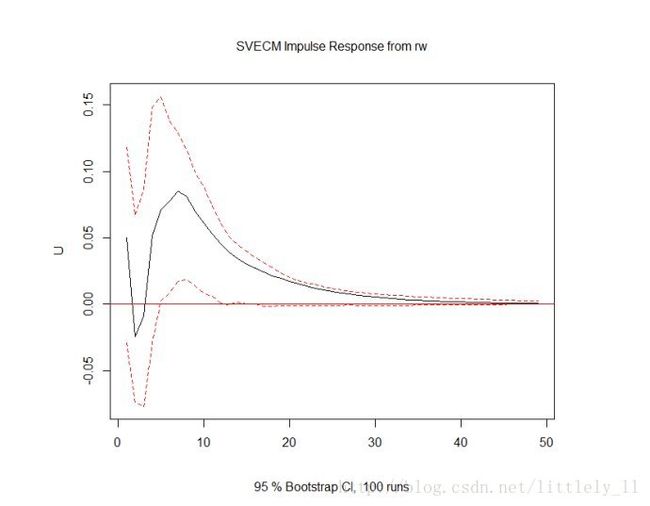
svec.irf<-irf(svec,response="U",n.ahead=48,boot=T)

plot(svec.irf)

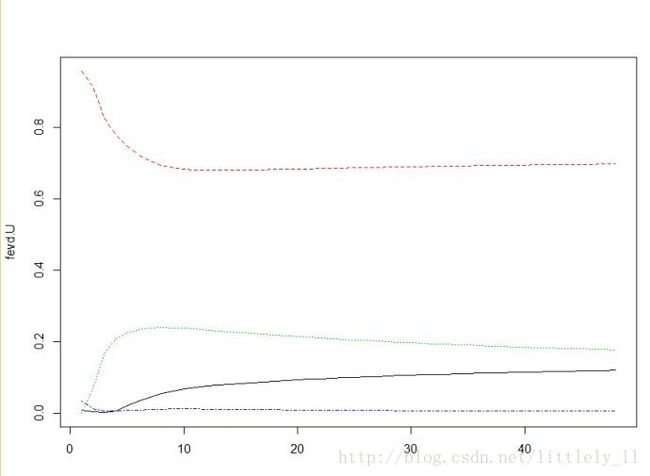
fevd.U<-fevd(svec,n.ahead=48)$U

matplot(fevd.U,type="l",lty=1:4)#失业率U的方差分解