【python科研绘图】绘制帕累托图(Pareto)步骤解析，并封装后直接调用

手动反爬虫： 原博地址 https://blog.csdn.net/lys_828/article/details/113746366

 知识梳理不易，请尊重劳动成果，文章仅发布在CSDN网站上，在其他网站看到该博文均属于未经作者授权的恶意爬取信息

如若转载，请标明出处，谢谢！

1 帕累托图

帕累托分析（贡献度分析） → 帕累托法则：20/80定律

“原因和结果、投入和产出、努力和报酬之间本来存在着无法解释的不平衡。一般来说，投入和努力可以分为两种不同的类型：多数，它们只能造成少许的影响；少数，它们造成主要的、重大的影响。”

比如：一个公司，80%利润来自于20%的畅销产品，而其他80%的产品只产生了20%的利润

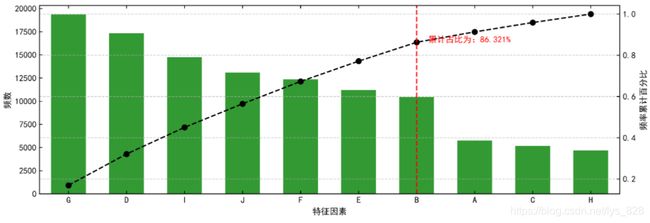
帕累托图基本构成：

• （1）双y轴图，左侧y轴表示频数，右侧y轴表示频率百分比，x轴表示特征因素
• （2）左侧y轴数据对应柱状图，右侧y轴数据对应点线图
• （3）点线图中超过80%的第一个因素进行标记，左侧就为核心特征因素

2 python实现

2.1 数据准备

程序运行前先导入相关的第三方库，代码是在jupyter notebook中运行。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

使用的数据采用随机数进行生成

data = pd.Series(np.random.randn(10)*5000 + 10000,
                   index = list('ABCDEFGHIJ'))
data

输出结果为：（每次运行生成的随机数的结果都会不一致）

A     5748.099899
B    10463.000272
C     5172.031773
D    17338.362775
E    11225.537785
F    12372.527636
G    19367.945373
H     4703.089439
I    14747.208553
J    13076.519903
dtype: float64

2.2 特征因素数值排序

数据的类型是Series数据，直接对值进行排序（由大到小）

data.sort_values(ascending=False,inplace = True)
data

输出结果为：

G    19367.945373
D    17338.362775
I    14747.208553
J    13076.519903
F    12372.527636
E    11225.537785
B    10463.000272
A     5748.099899
C     5172.031773
H     4703.089439
dtype: float64

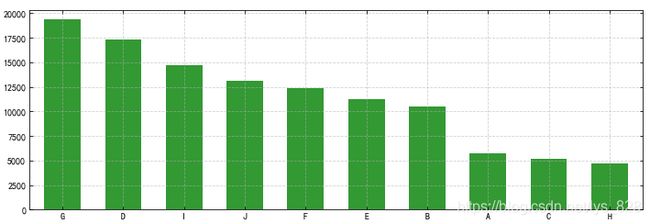
顺便也可以查看一下特征因素统计情况

#查看数据频数
plt.figure(figsize=(12,8))
data.plot(kind = 'bar', color = 'g', alpha = 0.8, width = 0.6,rot=0)

输出结果为：

2.3 计算累计频率百分比

上面计算了左侧y轴对应的频数，接下来就要计算右侧y轴对应的数据

#计算累计营收占比
p = data.cumsum()/data.sum()
p

输出结果为：（最后一个特征因素的结果一定为1）

G    0.169575
D    0.321381
I    0.450500
J    0.564991
F    0.673318
E    0.771603
B    0.863211
A    0.913539
C    0.958822
H    1.000000
dtype: float64

2.4 标记累计百分比80%特征因素的位置

上面求解出累计百分比的大小，这里标记的是百分比大于等于80%的第一个特征因素的位置

key = p[p>0.8].index[0]
key_num = data.index.tolist().index(key)
print('超过80%占比的节点值索引为：',key)
print('超过80%占比的节点值索引位置为：',key_num)

输出结果为：

超过80%占比的节点值索引为： B
超过80%占比的节点值索引位置为： 6

2.5 输出核心的特征因素信息

对于低于累计百分比80%的特征因素就是我们要筛选的结果

key_product = data.loc[:key]
print('核心产品为：')
print(key_product)

输出结果为：（索引在80%占比的节点值索引位置之前的内容）

核心产品为：
G    19367.945373
D    17338.362775
I    14747.208553
J    13076.519903
F    12372.527636
E    11225.537785
B    10463.000272
dtype: float64

2.6 绘制帕累托图

至此绘制帕累托图所需要的数据全部准备完毕，直接绘制

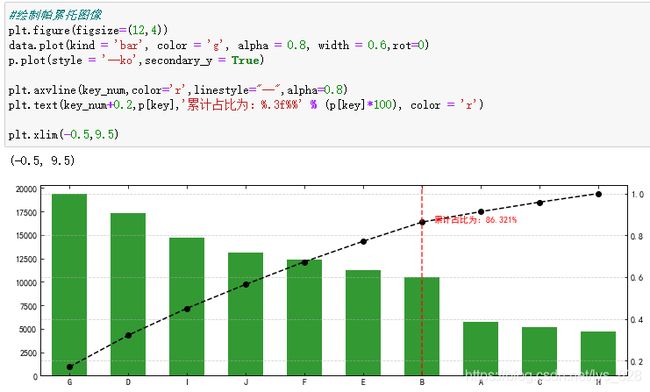
plt.figure(figsize=(12,4))
data.plot(kind = 'bar', color = 'g', alpha = 0.8, width = 0.6,rot=0)
p.plot(style = '--ko',secondary_y = True)

plt.axvline(key_num,color='r',linestyle="--",alpha=0.8)  
plt.text(key_num+0.2,p[key],'累计占比为：%.3f%%' % (p[key]*100), color = 'r') 

输出结果为：（基本上满足要求）

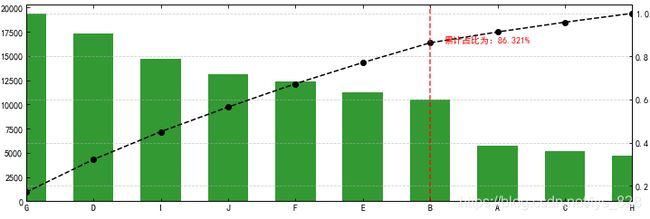
这里可以发现左右两侧只显示了一半的内容，可以通过plt.xlim()方法解决

3 封装

整个过程中梳理完毕后，发现共有三个功能需要实现，也就是2.4-2.6的部分，因此可以设置一个类， 添加三个函数，完成绘制帕累托图的代码封装。

直接给出代码，注意的是传入的数据是Series数据，因为对于DataFrame数据，单独取一列研究特征因素对应的数据类别就是Series数据

3.1 全部代码

class Pareto_analysis:
    
    def __init__(self,series_data):
        self.series_data = series_data
        
    def get_key_factor_location(self):
        data.sort_values(ascending=False,inplace = True)
        p = data.cumsum()/data.sum()
        key = p[p>0.8].index[0]
        key_num = data.index.tolist().index(key)
        print('超过80%占比的节点值索引为：',key)
        print('超过80%占比的节点值索引位置为：',key_num)
        
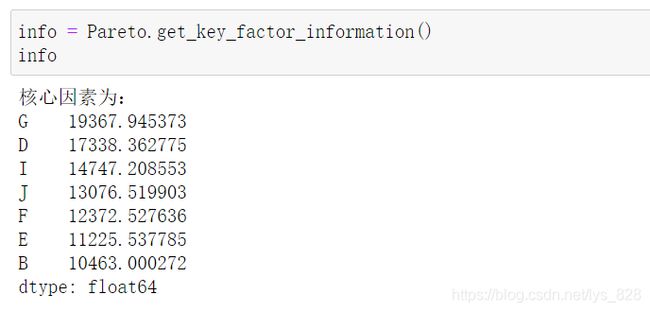
    def get_key_factor_information(self):
        key_product = data.loc[:key]
        print('核心因素为：')
        print(key_product)
        
    def plot_figure(self):
        plt.figure(figsize=(12,4),dpi=500)
        data.plot(kind = 'bar', color = 'g', alpha = 0.8, width = 0.6,rot=0)
        plt.ylabel('频数')
        plt.xlabel('特征因素')
        p.plot(style = '--ko',secondary_y = True)

        plt.axvline(key_num,color='r',linestyle="--",alpha=0.8)  
        plt.text(key_num+0.2,p[key],'累计占比为：%.3f%%' % (p[key]*100), color = 'r')  # 累计占比超过80%的节点
        plt.ylabel('频率累计百分比')
        #这里根据特征因素的数量进行边距的设置
        plt.xlim(-0.5,len(data)-0.5)

3.2 应用示例

（1）标记累计百分比80%特征因素的位置

（2）标记累计百分比80%特征因素的位置

（3）绘制帕累托图

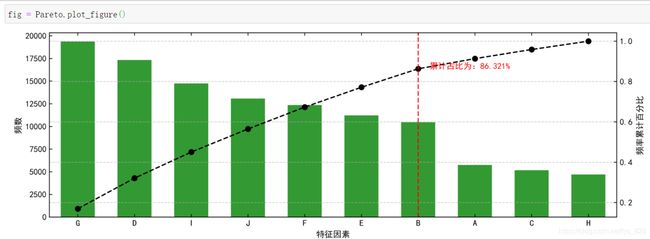
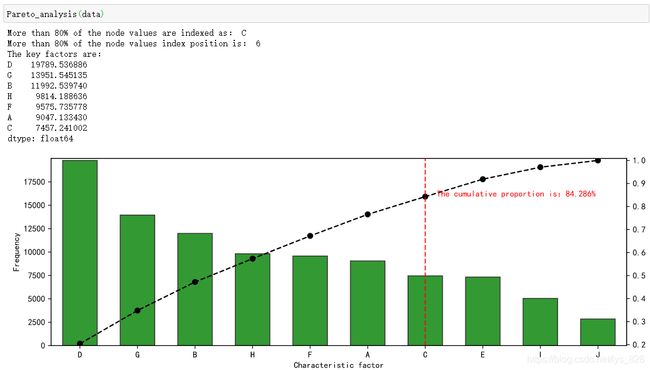
直接一个函数调用，不想整那么麻烦的话

def Pareto_analysis(data):
    data.sort_values(ascending=False,inplace = True)
    p = data.cumsum()/data.sum()
    key = p[p>0.8].index[0]
    key_num = data.index.tolist().index(key)
    print('More than 80% of the node values are indexed as：',key)
    print('More than 80% of the node values index position is：',key_num)

    key_product = data.loc[:key]
    print('The key factors are：')
    print(key_product)

    plt.figure(figsize=(12,4),dpi=500)
    data.plot(kind = 'bar', color = 'g',edgecolor = 'black', alpha = 0.8, width = 0.6,rot=0)
    plt.ylabel('Frequency')
    plt.xlabel('Characteristic factor')
    p.plot(style = '--ko',secondary_y = True)

    plt.axvline(key_num,color='r',linestyle="--",alpha=0.8)  
    plt.text(key_num+0.2,p[key],'The cumulative proportion is：%.3f%%' % (p[key]*100), color = 'r')  
    plt.ylabel('Cumulative percentages')

    plt.xlim(-0.5,len(data)-0.5)

调用函数，输出结果为：

至此利用python绘制帕累托图的过程就梳理完毕了！