经典机器学习方法（1）—— 线性回归

• 参考：动手学深度学习
• 注：本文是 jupyter notebook 文档转换而来，部分代码可能无法直接复制运行！

---

1. 线性回归

1.1 基础概念

• 线性回归，顾名思义，就是用线性模型来处理回归问题
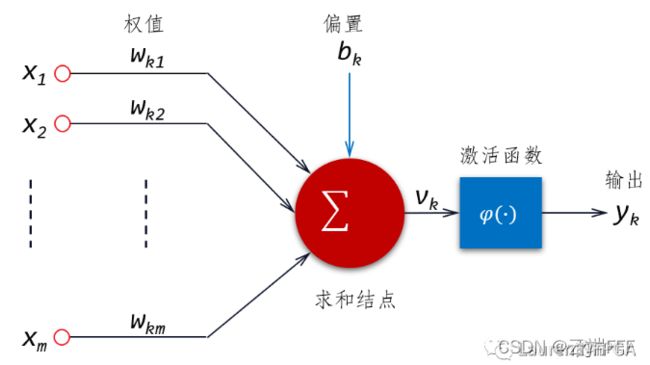
  1. 线性模型：使用样本特征的线性组合，加上偏置项作为预测标记。形式化地讲，对于样本 $x\text{x}x=\{x_1,x_2,...,x_n{\}}^{\top }$，设特征权重向量（weight）和偏置项（bias）分别为 $w\text{w}w=[w_1,w_2,...,w_n{]}^{\top }$ 和 $b$，标记预测为 $$\hat{y}={x\text{x}x}^{\top }w\text{w}w+b$$
  2. 回归问题：一种因变量为连续变量的函数估计问题。回归问题在实际中很常见，如预测房屋价格、气温、销售额等连续值预测问题

1.2 模型训练

• 模型：本质就是一个函数，是从样本到标签的映射。假设我们考虑的样本具有两个特征，即 $x\text{x}x=\{x_1,x_2\}$，则线性模型通过下式给出 $x\text{x}x$ 对应的标签 $\hat{y}$
  $$\hat{y}=x_1{w}_1+x_2{w}_2+b$$ 其中权重 $w_1,w_2$ 和偏置 $b$ 是模型参数，给定一组参数，即确定一个模型。当 $w_1,w_2,b$ 任取时，这个式子对应一组模型，称为 假设空间

• 模型训练：指通过数据，在假设空间中找到一个最优模型（或者说找一组最优参数确定的模型），使得（数据集外）任意样本 $x\text{x}x$ 的预测标记 $\hat{y}$ 尽量接近真实标记 $y$ 的过程

• 下面介绍模型训练所涉及的3个要素

1.2.1 训练数据

• 为了从假设空间中选出最优模型，首先需要收集一系列真实数据组成 训练集。比如我们收集房屋售价数据集，其中一栋房屋被称为一个 样本，真实售出价格叫作 标签，用来预测标签的因素叫作 特征，特征用来表征样本的特点
• 我们假设样本空间中的全体样本服从一个未知的分布 $\mathcal{D}$，训练集中的每个样本都是独立地从这个分布上采样获得的，即 独立同分布(independent and identically distributed，i.i.d)。通常训练样本越多，我们得到的关于 $\mathcal{D}$ 的信息越多，就越可能训练出泛化能力强的模型

1.2.2 损失函数

• 在模型训练中，我们需要衡量价格预测值与真实值之间的误差作为改进模型的指导，这个衡量误差的函数称为 损失函数，给定训练数据集，它仅与模型参数相关，因此我们将它记为关于模型参数的函数。一个常用的选择是平方函数，这时第 $i$ 个样本的误差表达式为
  $$l^i(w_1,w_2,b)=\frac{1}{2}({\hat{y}}^i-y^i{)}^2$$ 其中 $\frac{1}{2}$ 是为了求导后常数为1，这样形式上稍微简单一些
• 通常使用训练数据集上所有样本的平均误差衡量模型的预测质量，即
  $$l(w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n{l}^i(w_1,w_2,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}(x_1^i{w}_1+x_2^i{w}_2+b-y^i{)}^2$$
• 训练的目标是找出使得损失最小化的最优模型参数，即
  $$w_1^{\ast },w_2^{\ast },b^{\ast }=\arg \underset{w_1,w_2,b}{\min }l(w_1,w_2,b)$$ 由于数据具有 i.i.d 性质，所以在训练集上优化得到的模型，也能在训练集以外的数据上有一定的性能保证

1.2.3 优化算法

• 优化算法就是求解优化问题的方法，针对不同问题，使用不同的方法，可以得到解析解或数值解

  1. 当模型和损失函数形式较为简单时，损失最小化问题可以直接求解，这类解叫作 解析解。上述使用平方损失的线性回归模型就属于这个范畴，可以使用最小二乘法求解，参考：一文看懂最小二乘法
  2. 然而，大多数深度学习模型并没有解析解，只能使用梯度下降等迭代式优化算法，通过有限次迭代模型参数来尽可能降低损失函数的值，这类解叫作 数值解

• 深度学习训练使用的优化算法通常有以下几种，参考 批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解

  1. 批量梯度下降（Batch Gradient Descent，BGD）
  2. 随机梯度下降（Stochastic Gradient Descent，SGD）
  3. 小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

  其中小批量随机梯度下降（mini-batch stochastic gradient descent）使用最为广泛。它的思想很简单

  1. 随机选取一组模型参数的初始值，准备训练数据集 $\mathcal{D}$
  2. 随机均匀采样 batch_size 个训练数据样本组成小批量（mini-batch）数据 $\mathcal{B}$
  3. 求 $\mathcal{B}$ 中数据本的平均损失有关模型参数的梯度，乘上 学习率 $\eta$ 做梯度下降来优化模型参数，即
     $$\begin{array}{rl}& w_1\leftarrow w_1-\eta \frac{\partial l(w_1,w_2,b)}{\partial w_1}=w_1-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial l^i(w_1,w_2,b)}{\partial w_1}\\ & w_2\leftarrow w_2-\eta \frac{\partial l(w_1,w_2,b)}{\partial w_2}=w_2-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial l^i(w_1,w_2,b)}{\partial w_2}\\ & b\leftarrow b-\eta \frac{\partial l(w_1,w_2,b)}{\partial b}=b-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial l^i(w_1,w_2,b)}{\partial b}\end{array}$$
  4. 迭代执行 2,3 两步直到模型收敛

1.3 模型预测

• 训练完成后，将优化算法停止时的模型参数记作 $\widehat{w_1},\widehat{w_2},\hat{b}$，它们是对最优参数 $w_1^{\ast },w_2^{\ast },b^{\ast }$ 的一个近似
• 学得的参数确定了一个线性模型，可以用来预测数据集外任意样本 $x\text{x}x=\{x_1,x_2\}$ 的标签，即
  $$\hat{y}=x_1\widehat{w_1}+x_2\widehat{w_2}+\hat{b}$$

1.4 线性回归的表示方法

1.4.1 神经网络图

• 线性模型可以看作神经网络中一个使用 Identity 函数作为激活函数的神经元，如下所示
  

• 深度学习中，神经网络图可以直观地表现模型结构，线性回归模型可以看作一个只有单一神经元的神经网络，其神经网络图如下所示（隐去了模型参数权重和偏差）
  

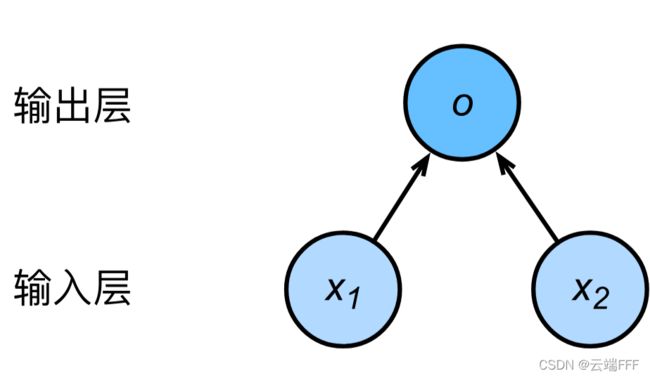
  1. 样本具有两个特征，所以输入层单元个数为2
  2. 输出层的计算单元即为上述的神经元，使用输出 $o$ 直接作为模型输出，即 $\hat{y}=o$
  3. 由于输入层不涉及计算，按照惯例，这个神经网络的层数为 1
  4. 由于输出层中的神经元和输入层中各个输入完全连接，这里的输出层是全连接层

  综上分析，回归模型一个单层全连接神经网络

1.4.2 向量表示

• 设每个样本有 $m$ 个特征，mini-batch 数据集 $\mathcal{B}$ 大小为 $n$，即
  $$\begin{array}{rl}& \widehat{y\text{y}y}=\left[\begin{array}{c}\widehat{y_1}\\ \widehat{y_2}\\ ⋮\\ \widehat{y_n}\end{array}\right],X\text{X}X=\left[\begin{array}{c}{x}_1\text{x1}{x}_1\\ x_2\text{x2}{x}_2\\ ⋮\\ x_n\text{xn}{x}_n\end{array}\right]=\left[\begin{array}{cccc}{x}_1^1& x_1^2& \dots & x_1^m\\ x_2^1& x_2^2& \dots & x_2^m\\ ⋮& ⋮& \ddots & ⋮\\ x_n^1& x_n^2& \dots & x_n^m\end{array}\right],w\text{w}w=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_m\end{array}\right]\end{array}$$ 线性模型在数据集上做预测的式子可如下表示为向量计算
  $$\widehat{y\text{y}y}=X\text{X}Xw\text{w}w+b\text{b}b$$
• 设模型参数为 $\theta \text{θ}\theta =[w_1,w_2,...,w_m,b{]}^{\top }$，损失函数可以重写为
  $$l(\theta \text{θ}\theta )=\frac{1}{2n}(\widehat{y\text{y}y}-y\text{y}y{)}^{\top }(\widehat{y\text{y}y}-y\text{y}y)$$ mini-batch 梯度下降的更新公式可以写作
  $$\theta \text{θ}\theta \leftarrow \theta \text{θ}\theta -\eta {▽}_{\theta }l(\theta \text{θ}\theta )=\theta \text{θ}\theta -\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{▽}_{\theta }{l}^i(\theta \text{θ}\theta )$$

2. 实现线性回归

2.1 数据准备

2.1.1 生成数据集

• 设训练数据集样本数为 1000，特征数为 2。随机生成批量样本 $X\text{X}X\in {\mathbb{R}}^{1000\times 2}$，其中任意 ${x\text{x}x}_i=\{x_{i_1},x_{i_2}\}\in X\text{X}X$，有 $x_{i_1},x_{i_2}\sim N(0,1)$
• 使用权重 $w\text{w}w=[-2,3.4{]}^{\top }$，偏差 $b=4.2$，含一个随机噪声项 $ϵ\sim N(0,0.01)$ 的线性模型来生成样本标签。使用向量表示为 $${y\text{y}y}_{1000\times 1}={X\text{X}X}_{1000\times 2}{w\text{w}w}_{2\times 1}+b\text{b}b+ϵ$$ 注意这里向量和标量相加使用了广播机制

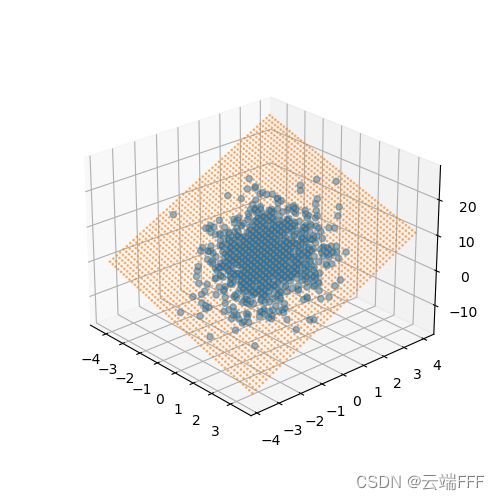
  %matplotlib notebook
  import torch
  from IPython import display
  from matplotlib import pyplot as plt
  import numpy as np
  import random
  
  # 生成样本
  num_inputs = 2
  num_examples = 1000
  true_w = torch.Tensor([-2,3.4]).view(2,1)
  true_b = 4.2
  
  # 1000 个2特征样本，每个特征都服从 N(0,1)
  features = torch.randn(num_examples, num_inputs,
                         dtype=torch.float32) 
  
  # 生成真实标记
  labels = torch.mm(features,true_w) + true_b
  labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                         dtype=torch.float32)
  

• 如下查看生成的数据集，它是采样自三维空间中的一个平面

  # 生成特征features[:, 1]和标签 labels 的散点图，直观地观察两者间的线性关系
  fig = plt.figure(figsize = (10,3.3))
  # 三维视图
  a0 = fig.add_subplot(1,3,1,label='a0',projection='3d') 
  a0.scatter(features[:, 0].numpy(),features[:, 1].numpy(),labels.numpy(),alpha=0.5)  # alpha透明度，c颜色序列
  
  # 投影到第 0 维度
  a1 = fig.add_subplot(1,3,2,label='a1') 
  a1.scatter(features[:, 0].numpy(),labels.numpy(),alpha=0.5)  
  
  # 投影到第 1 维度
  a2 = fig.add_subplot(1,3,3,label='a2') 
  a2.scatter(features[:, 1].numpy(),labels.numpy(),alpha=0.5)  
  

2.1.2 读取数据

• 训练过程中，每轮迭代使用 mini-batch 的数据更新参数，我们构造一个生成器，每次访问取指定的 batch_size 个数据返回

  def data_iter(batch_size, features, labels):
      num_examples = len(features)
      indices = list(range(num_examples))
      random.shuffle(indices) # 样本的读取顺序是随机的，打乱一下
      
      # 使用 yield 关键字将此函数转为生成器，每次访问取 batch_size 数据返回
      for i in range(0, num_examples, batch_size):
          j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
          yield  features.index_select(0, j), labels.index_select(0, j)
  

• 测试一下

  # 取一个 mini-batch 测试
  batch_size = 4
  for X, y in data_iter(batch_size, features, labels):
      print(X)
      print(y)
      break
  '''
  tensor([[ 1.3587, -1.3951],
          [-0.8161, -0.7696],
          [ 0.7647, -0.3447],
          [-0.2530,  0.9908]])
  tensor([[-3.2561],
          [ 3.2275],
          [ 1.5034],
          [ 8.0875]])
  '''
  

2.2 模型设计

• 模型参数初始化

  1. $w_i\sim N(0,0.01^2),i=1,2$
  2. $b=0$

  注意设置属性 requires_grad = True，这样在后续训练过程中才能对这些参数求梯度并迭代更新参数值

  w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32, requires_grad=True)
  b = torch.zeros(1, dtype=torch.float32, requires_grad=True)
  

• 模型定义为线性函数

  def linreg(X, w, b):  
      return torch.mm(X, w) + b
  

• 损失函数使用平方损失，第 $i$ 个样本的损失为
  $$l^i(w_1,w_2,b)=\frac{1}{2}({\hat{y}}^i-y^i{)}^2$$

  设置常数 $\frac{1}{2}$ 是为了使对平方项求导后的常数系数为1，这样在形式上稍微简单一些。另外在实现中要注意保持 $y$ 和 $\hat{y}$ 具有一致的形状

  def squared_loss(y_hat, y): 
      return (y_hat - y.view(y_hat.size())) ** 2 / 2 # 注意这里返回的是向量, 另外, pytorch里的 MSELoss 默认不是除2，而是除以 batch_size
  

• 优化算法使用 mini-batch 梯度下降

  def mbgd(params, lr, batch_size):
      for param in params:
          param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
  

2.3 模型训练

• 注意我们使用 mini-batch 梯度下降作为优化算法，这意味着每轮迭代中，通过以下三步执行一个 batch 的训练

  1. 从数据集中采样 mini_batch 数量的样本构成 mini-batch $\mathcal{B}$
  2. 计算 mini-batch 上线性模型各个参数的梯度，比如 $w_1$ 的梯度为
     $${▽}_{w_1}=\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\frac{\partial l^i(w_1,w_2,b)}{\partial w_1}=\frac{\eta }{|\mathcal{B}|}\frac{\partial {\sum }_{i\in \mathcal{B}}{l}^i(w_1,w_2,b)}{\partial w_1}$$
  3. 更新各参数值，比如 $w_1$ 参数如下更新
     $$w_1\leftarrow w_1-\frac{\eta }{|\mathcal{B}|}\frac{\partial {\sum }_{i\in \mathcal{B}}{l}^i(w_1,w_2,b)}{\partial w_1}$$

• 连续执行 $\frac{\text{num\_examples}}{\text{mini\_batch}}$ 个 batch 后，称为执行了一个 epoch，这代表将训练数据集中所有样本都使用了一次（假设样本数能够被批量大小整除）

• 这里的迭代周期个数 num_epochs 和学习率 lr 都是超参数，分别设为 num_epochs = 3 和 lr = 0.03。在实践中，大多超参数都需要通过反复试错来不断调节

  lr = 0.03
  num_epochs = 3
  net = linreg
  loss = squared_loss
  batch_size = 10
  
  # 总共训练 num_epochs 个 epoch
  for epoch in range(num_epochs):  
      # 在每一个迭代周期中，会使用训练数据集中所有样本一次
      # X和y分别是mini-batch样本的特征和标签
      for X, y in data_iter(batch_size, features, labels):
          y_hat = net(X, w, b)
          l = loss(y_hat, y).sum()      # l是有关小批量X和y的损失
          l.backward()                  # 小批量的损失对模型参数求梯度
          mbgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数
  
          # 不要忘了梯度清零
          w.grad.data.zero_()
          b.grad.data.zero_()
      train_l = loss(net(features, w, b), labels)
      print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
  '''
  epoch 1, loss 0.036538
  epoch 2, loss 0.000134
  epoch 3, loss 0.000053
  '''
  

• 如下查看拟合得到的平面

  # 生成特征features[:, 1]和标签 labels 的散点图，直观地观察两者间的线性关系
  fig = plt.figure(figsize = (5,5))
  a0 = fig.add_subplot(label='a0',projection='3d') 
  a0.scatter(features[:, 0].numpy(),features[:, 1].numpy(),labels.numpy(),alpha=0.5)  # alpha透明度，c颜色序列
  
  xlim,ylim = a0.get_xlim(),a0.get_ylim()
  axisx,axisy = np.linspace(xlim[0],xlim[1],50),np.linspace(ylim[0],ylim[1],50)
  axisy,axisx = np.meshgrid(axisy,axisx)
  xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
  y_hat = net(torch.from_numpy(xy).float(), w, b).detach().numpy()
  a0.scatter(xy[:,0],xy[:,1], y_hat.T[0],s=1,alpha=0.5,cmap="rainbow") 
  

2.4 完整代码

• 整合上述过程，给出完整代码

  import torch
  from IPython import display
  from matplotlib import pyplot as plt
  import numpy as np
  import random
  
  # 生成样本
  num_inputs = 2
  num_examples = 1000
  true_w = torch.Tensor([-2,3.4]).view(2,1)
  true_b = 4.2
  
  # 1000 个2特征样本，每个特征都服从 N(0,1)
  features = torch.randn(num_examples, num_inputs,
                         dtype=torch.float32) 
  
  # 生成真实标记
  labels = torch.mm(features,true_w) + true_b
  labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                         dtype=torch.float32)
  
  # 模型初始参数
  w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32, requires_grad=True)
  b = torch.zeros(1, dtype=torch.float32, requires_grad=True)
  
  # 读取数据
  def data_iter(batch_size, features, labels):
      num_examples = len(features)
      indices = list(range(num_examples))
      random.shuffle(indices) # 样本的读取顺序是随机的，打乱一下
      
      # 使用 yield 关键字将此函数转为迭代器，每次访问取 batch_size 数据返回
      for i in range(0, num_examples, batch_size):
          j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
          yield  features.index_select(0, j), labels.index_select(0, j)
  
  # 模型
  def linreg(X, w, b):  
      return torch.mm(X, w) + b
  
  # 损失函数
  def squared_loss(y_hat, y): 
      return (y_hat - y.view(y_hat.size())) ** 2 / 2 # 注意这里返回的是向量, 另外, pytorch里的 MSELoss 默认不是除2，而是除以 batch_size
  
  # 优化方法使用小批量梯度下降
  def mbgd(params, lr, batch_size):
      for param in params:
          param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
  
  
  lr = 0.03               # 学习率
  num_epochs = 3          # 训练轮数
  net = linreg            # 模型
  loss = squared_loss     # 损失函数
  batch_size = 10         # 小批量梯度下降中batch尺寸
  
  # 总共训练 num_epochs 个 epoch
  for epoch in range(num_epochs):  
      # 在每一个迭代周期中，会使用训练数据集中所有样本一次
      # X和y分别是mini-batch样本的特征和标签
      for X, y in data_iter(batch_size, features, labels):
          y_hat = net(X, w, b)
          l = loss(y_hat, y).sum()      # l是有关小批量X和y的损失
          l.backward()                  # 小批量的损失对模型参数求梯度
          mbgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数
  
          # 不要忘了梯度清零
          w.grad.data.zero_()
          b.grad.data.zero_()
      train_l = loss(net(features, w, b), labels)
      print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
  
  
  # 生成特征features[:, 1]和标签 labels 的散点图，直观地观察两者间的线性关系
  fig = plt.figure(figsize = (5,5))
  a0 = fig.add_subplot(label='a0',projection='3d') 
  a0.scatter(features[:, 0].numpy(),features[:, 1].numpy(),labels.numpy(),alpha=0.5)  # alpha透明度，c颜色序列
  
  xlim,ylim = a0.get_xlim(),a0.get_ylim()
  axisx,axisy = np.linspace(xlim[0],xlim[1],50),np.linspace(ylim[0],ylim[1],50)
  axisy,axisx = np.meshgrid(axisy,axisx)
  xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
  y_hat = net(torch.from_numpy(xy).float(), w, b).detach().numpy()
  a0.scatter(xy[:,0],xy[:,1], y_hat.T[0],s=1,alpha=0.5,cmap="rainbow") 
  
  plt.show()
  

3. 利用 Pytorch 简洁地实现线性回归

• 前面我们手动实现了线性回归的模型计算过程，当模型变得复杂时，手动实现会非常繁琐。前文 1.4.1 节已经说明，可以把线性回归模型看做一个单层全连接神经网络，而 pytorch 中提供了大量预定义的神经网络层，常用损失函数及优化器，可以大大简化线性回归模型的实现

3.1 数据准备

3.1.1 生成数据集

• 与上一节相同

3.1.2 读取数据

• 使用 torch.utils.data 中提供的方法实现batch数据获取

  import torch.utils.data as Data
  
  batch_size = 4
  
  # 包装数据集，将训练数据的特征和标签组合
  dataset = Data.TensorDataset(features, labels)
  
  # 构造迭代器，可以随机读取小批量
  data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
  

  for X, y in data_iter:
      print(X)
      print(y)
      break
  '''
  tensor([[ 1.7174,  0.8377],
          [ 0.4138, -1.0372],
          [-0.3596,  0.0313],
          [-0.2548,  0.8188]])
  tensor([[ 3.6061],
          [-0.1535],
          [ 5.0350],
          [ 7.4860]])
  '''
  

• 这里用到了两个方法

  1. torch.utils.data.TensorDataset(features, labels)：类似 python 中的 zip 功能，对 Tensor 进行打包，返回的 TensorDataset 对象实例可以索引和取长度等。该类通过每一个 tensor 的第一个维度进行索引，因此要求打包的两个 tensor 第一维度必须相等
  2. torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)：把上一个方法打包好的数据集和采样器相结合，返回一个迭代器，每次调用返回 batch_size 对 dataset 中数据，通过 shuffle 参数控制返回数据时是否打乱，另外还可以实现多进程、不同采样策略，数据校对等等处理过程

  可以借助一下代码理解这两个方法，参考 pytorch的nn.MSELoss损失函数返回值介绍

  a = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9], [0,0,0], [6,6,6]])
  b = torch.tensor([44, 55, 66, 11, 88])
  train_ids = TensorDataset(a, b) 
  # 切片输出
  print(train_ids[0:2])
  print('=' * 80)
  
  # 循环取数据
  for x_train, y_label in train_ids:
      print(x_train, y_label)
  
  # DataLoader进行数据封装
  print('=' * 80)
  train_loader = DataLoader(dataset=train_ids, batch_size=4, shuffle=True)
  for i, data in enumerate(train_loader, 1):  
      x_data, label = data
      print(' batch:{0} x_data:{1}  label: {2}'.format(i, x_data, label))
      
  '''
  (tensor([[1, 2, 3],
          [4, 5, 6]]), tensor([44, 55]))
  ================================================================================
  tensor([1, 2, 3]) tensor(44)
  tensor([4, 5, 6]) tensor(55)
  tensor([7, 8, 9]) tensor(66)
  tensor([0, 0, 0]) tensor(11)
  tensor([6, 6, 6]) tensor(88)
  ================================================================================
   batch:1 x_data:tensor([[0, 0, 0],
          [1, 2, 3],
          [7, 8, 9],
          [4, 5, 6]])  label: tensor([ 11, 44, 66, 55])
   batch:2 x_data:tensor([[6, 6, 6]])  label: tensor([88])
  '''
  

3.2 模型设计

3.2.1 定义模型

• 搭建网络需要用到 import torch.nn 模块，“nn”就是 neural networks（神经网络）的缩写，该模块定义了大量神经网络的层，由于内部使用了 autograd 机制，可以进行反向传播来优化参数
• nn 的核心数据结构是 Module，这是一个抽象概念，可以表示
  1. 神经网络中的某个层（layer）
  2. 一个包含很多层的神经网络

3.2.1.1 手动编写网络

• 在实际使用中，最常见的做法是继承 nn.Module，撰写自己的网络/层。一个 nn.Module 实例应该包含

  1. 一些层
  2. forward 方法，执行前向传播，返回模型输出

  示例如下

  import torch.nn as nn
  
  class LinearNet(nn.Module):
      def __init__(self, n_feature):
          super(LinearNet, self).__init__()
          # 定义一个全连接层
          self.linear = nn.Linear(n_feature, 1)
      
      # 前向传播方法
      def forward(self, x):
          y = self.linear(x)
          return y
  
  net = LinearNet(num_inputs)
  print(net) # 使用print可以打印出网络的结构
  
  '''
  LinearNet(
    (linear): Linear(in_features=2, out_features=1, bias=True)
  )
  '''
  

  观察打印出的网络结构，其中 in_features 代表输入维度，out_features 代表输出维度，bias 代表是否增加偏置项。设样本数为 $n$，nn.Linear 模型公式为
  $${X\text{X}X}_{n\times in}{W\text{W}W}_{in\times out}+{b\text{b}b}_{1\times out}={Y\text{Y}Y}_{n\times out}$$ 这里向量 $b\text{b}b$ 和矩阵 $XW\text{XW}XW$ 相加，使用了广播机制

  • 注意：torch.nn 仅支持输入一个batch的样本不支持单个样本输入，如果只有单个样本，可使用 input.unsqueeze(0) 来添加一维

3.2.1.2 利用 Sequential 容器搭建网络

• 使用 nn.Sequential 可以更方便地搭建网络，Sequential 是一个有序的容器，网络层将按照在传入 Sequential 的顺序依次被添加到计算图中

  # 写法一
  net = nn.Sequential(
      nn.Linear(num_inputs, 1)
      # 此处还可以传入其他层
      )
  
  # 写法二
  net = nn.Sequential()
  net.add_module('linear', nn.Linear(num_inputs, 1))
  # net.add_module ......
  
  # 写法三
  from collections import OrderedDict
  net = nn.Sequential(OrderedDict([
            ('linear', nn.Linear(num_inputs, 1))
            # ......
          ]))
  
  
  print(net)
  print(net[0])
  '''
  Sequential(
    (linear): Linear(in_features=2, out_features=1, bias=True)
  )
  Linear(in_features=2, out_features=1, bias=True)
  '''
  

  • 注意，使用这种方式构造的网络，要想访问其中某个 Module，必须用索引的方式将其取出来，比如这里要 net[0] 和 3.2.1.1 节中的 net 等价

• 可以通过 net.parameters() 来查看模型所有的可学习参数，此函数将返回一个生成器

  parameters = net.parameters()
  for param in parameters:
      print(param)
  '''
  Parameter containing:
  tensor([[0.0016, 0.5458]], requires_grad=True)
  Parameter containing:
  tensor([0.7041], requires_grad=True
  '''
  

• 注：我们使用这种方式搭建线性回归模型，后面统一使用 net[0] 写法

3.2.2 参数初始化

• PyTorch 的 init 模块中提供了多种参数初始化方法。这里参数设置同 2.2 节
  1. $w_i\sim N(0,0.01^2),i=1,2$，使用 init.normal_ 方法将实现
  2. $b=0$，使用 init.constant_ 方法实现

  from torch.nn import init
  
  init.normal_(net[0].weight, mean=0, std=0.01)
  init.constant_(net[0].bias, val=0)  # 也可以直接修改bias的data: net[0].bias.data.fill_(0)
  

  注：如果这里的 net 是没使用 nn.Sequential 直接定义的，那么上面代码会报错，net[0].weight 应改为 net.linear.weight，bias 亦然

3.2.3 损失函数

• PyTorch torch.nn 模块中提供了各种损失函数，这些损失函数可看作是一种特殊的层，它们被实现为 nn.Module 的子类
• 这里我们现在使用 nn 模型提供的均方误差损失类 nn.MSELoss() 作为模型的损失函数，构造它的对象实例 loss。注意默认情况下这个 MSE loss 计算过程中取平均值了

  loss = nn.MSELoss()
  

3.2.4 优化算法

• Pytorch torch.optim 模块提供了很多常用的优化算法，如SGD、Adam和RMSProp等
• 这里我们使用学习率为指定为 0.03 的随机梯度下降（SGD）优化器来优化 net 的所有参数

  • 这里的 SGD，如果你去看 pytorch 的源码，会发现它只是在根据 loss 计算所有参数对应的梯度，而 loss 是根据我们选取的 batch 样本计算的，所以本质还是 mini-batch GD。
  • 另外，源码在调整参数值时似乎没有除以 batch_size，这可能是因为我们选择的 nn.MSELoss() 在默认情况下是返回 batch 样本的平均 loss，所以算出的梯度不再需要除 batch_size

  import torch.optim as optim
  
  optimizer = optim.SGD(net.parameters(), lr=0.03)
  print(optimizer)
  '''
  SGD (
  Parameter Group 0
      dampening: 0
      lr: 0.03
      momentum: 0
      nesterov: False
      weight_decay: 0
  )
  '''
  

• 可以为不同子网络设置不同的学习率，这在 finetune 时经常用到，例如

  optimizer =optim.SGD([
                  # 如果对某个参数不指定学习率，就使用最外层的默认学习率
                  {'params': net.subnet1.parameters()}, # lr=0.03
                  {'params': net.subnet2.parameters(), 'lr': 0.01}
              ], lr=0.03, momentum=0.9)
  

  1. subnet1 学习率设为 0.03
  2. subnet2 学习率设为 0.01
  3. 所有网络动量都设为 0.9
• 有时候我们不想让学习率固定成一个常数，主要有两种做法
  1. 修改 optimizer.param_groups 中对应的学习率

     # 调整学习率
     for param_group in optimizer.param_groups:
         param_group['lr'] *= 0.1 # 学习率为之前的0.1倍
     

  2. 新建优化器。由于 optimizer 十分轻量级，构建开销很小，故而可以构建新的 optimizer。虽然对于使用动量的优化器（如Adam），会丢失动量等状态信息，可能导致损失函数的收敛出现震荡等情况，但我们通常使用这种方式

3.3 模型训练

• 训练过程如下所示

  num_epochs = 3
  for epoch in range(1, num_epochs + 1):
      for X, y in data_iter:
          output = net(X) 
          l = loss(output, y.view(-1, 1))  # y.view(-1,1) 代表第一维度大小随第二维度大小确定
          optimizer.zero_grad()            # 梯度清零，等价于 net.zero_grad()
          l.backward()                     # 计算各参数梯度
          optimizer.step()                 # 优化一步
      print('epoch %d, loss: %f' % (epoch, l.item()))
  
  '''
  epoch 1, loss: 0.000081
  epoch 2, loss: 0.000096
  epoch 3, loss: 0.000098
  '''
  

• 如下查看拟合得到的平面

  # 生成特征features[:, 1]和标签 labels 的散点图，直观地观察两者间的线性关系
  fig = plt.figure(figsize = (5,5))
  a0 = fig.add_subplot(label='a0',projection='3d') 
  a0.scatter(features[:, 0].numpy(),features[:, 1].numpy(),labels.numpy(),alpha=0.5)  # alpha透明度，c颜色序列
  
  xlim,ylim = a0.get_xlim(),a0.get_ylim()
  axisx,axisy = np.linspace(xlim[0],xlim[1],50),np.linspace(ylim[0],ylim[1],50)
  axisy,axisx = np.meshgrid(axisy,axisx)
  xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
  y_hat = net(torch.from_numpy(xy).float()).detach().numpy()
  a0.scatter(xy[:,0],xy[:,1], y_hat.T[0],s=1,alpha=0.5,cmap="rainbow") 
  

3.4 完整代码

• 整合上述过程，给出完整代码

  import torch
  from IPython import display
  from matplotlib import pyplot as plt
  import numpy as np
  import random
  import torch.utils.data as Data
  import torch.nn as nn
  import torch.optim as optim
  
  # 生成样本
  num_inputs = 2
  num_examples = 1000
  true_w = torch.Tensor([-2,3.4]).view(2,1)
  true_b = 4.2
  batch_size = 10
  
  # 1000 个2特征样本，每个特征都服从 N(0,1)
  features = torch.randn(num_examples, num_inputs,
                         dtype=torch.float32) 
  
  # 生成真实标记
  labels = torch.mm(features,true_w) + true_b
  labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                         dtype=torch.float32)
  
  # 包装数据集，将训练数据的特征和标签组合
  dataset = Data.TensorDataset(features, labels)
  
  # 构造迭代器，可以随机读取小批量
  data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
  
  # 定义模型
  net = nn.Sequential(
      nn.Linear(num_inputs, 1)
      )
  
  # 初始化模型参数
  nn.init.normal_(net[0].weight, mean=0, std=0.01)
  nn.init.constant_(net[0].bias, val=0)  # 也可以直接修改bias的data: net[0].bias.data.fill_(0)
  
  # 均方差损失函数对象实例
  loss = nn.MSELoss()
  
  # SGD优化器对象实例
  optimizer = optim.SGD(net.parameters(), lr=0.03)
  
  # 模型训练
  num_epochs = 3
  for epoch in range(1, num_epochs + 1):
      for X, y in data_iter:
          output = net(X) 
          l = loss(output, y.view(-1, 1))  # y.view(-1,1) 代表第一维度大小随第二维度大小确定
          optimizer.zero_grad()            # 梯度清零，等价于net.zero_grad()
          l.backward()                     # 计算各参数梯度
          optimizer.step()                 # 优化一步
      print('epoch %d, loss: %f' % (epoch, l.item()))
  
  
  # 生成特征features[:, 1]和标签 labels 的散点图，直观地观察两者间的线性关系
  fig = plt.figure(figsize = (5,5))
  a0 = fig.add_subplot(label='a0',projection='3d') 
  a0.scatter(features[:, 0].numpy(),features[:, 1].numpy(),labels.numpy(),alpha=0.5)  # alpha透明度，c颜色序列
  
  xlim,ylim = a0.get_xlim(),a0.get_ylim()
  axisx,axisy = np.linspace(xlim[0],xlim[1],50),np.linspace(ylim[0],ylim[1],50)
  axisy,axisx = np.meshgrid(axisy,axisx)
  xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
  y_hat = net(torch.from_numpy(xy).float()).detach().numpy()
  a0.scatter(xy[:,0],xy[:,1], y_hat.T[0],s=1,alpha=0.5,cmap="rainbow") 
  
  plt.show()