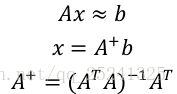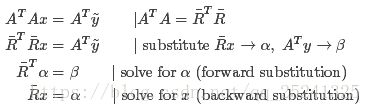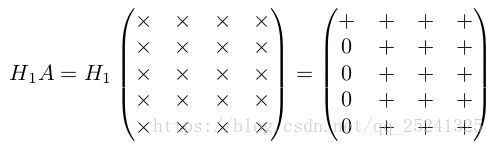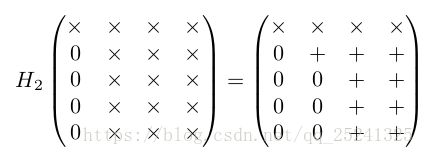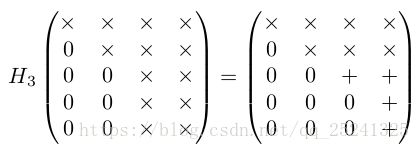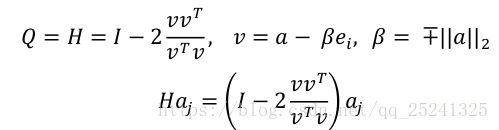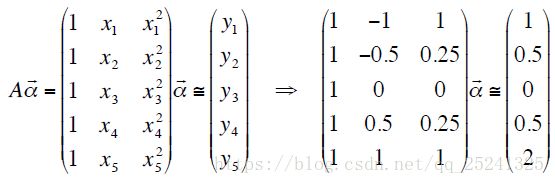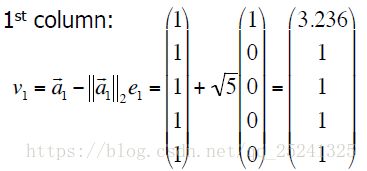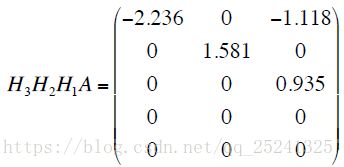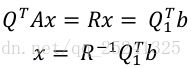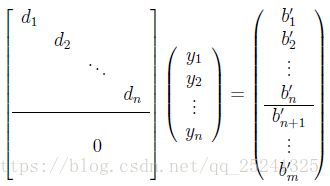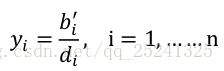算法解析：线性最小二乘问题

本篇博客主要讲解线性最小二乘问题，主要包括以下内容：

• 最小二乘问题的定义
• 正规方程求解
• 乔姆斯基分解法求解
• QR分解法求解
• 奇异值分解法求解
• 齐次方程的最小二乘

一. 问题的定义

　　最小二乘问题通常可以表述为,通过搜集到的一些数据(获取得到的样本),对某一个模型进行拟合,并尽可能的使得模型结果和样本达到某种程度上的最佳拟合:

　　转化为数学表达式为:

　　其中 x 为模型中参数所组成的向量,e 通常被称为残差向量(residual vector).
　　现在假设我们的模型函数为 Ax,样本为 b 且方程数大于未知量数则有:
　　转化为最小二乘表达式为:
　　该方程通常可以通过正规方程、QR 分解、乔姆斯基分解(Cholesky decomposition)和奇异值分解(SVD)等方法求解。

二. 求解方法

       2.1. 正规方程(Normal Equation)

将展开可以得到:
为了求解得到该方程的最优解(即最小值),我们可以求解其对于参数 x 的偏导数,并令其等于零: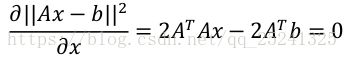
化简后得到:
以上被称为最小二乘的正规方程(Normal Equation)。进一步求解可得到:
该结果亦可表示为矩阵的伪逆形式(伪逆为逆矩阵广义形式,奇异阵或非方阵不存在逆矩阵,但可以求解其伪逆矩阵)

       2.2. 乔姆斯基分解(Cholesky Decomposition)

以下内容参考[1].
由于简单的正规方程计算运算量,因此为了更快更稳定的求解,通常可以运用乔姆斯基分解进行求解。
对正规矩阵左侧进行乔姆斯基分解有:

该乔姆斯基分解会生成一个上三角矩阵 R ̄ 和它的转置矩阵,所以我们能够通过连续的向前和向后的替换来计算求解向量:

       2.3. QR分解

以下图片参考[4]

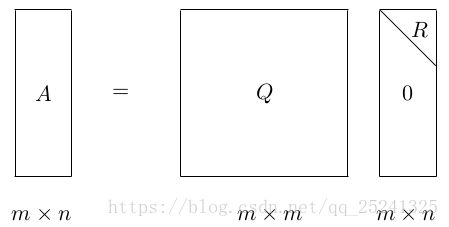
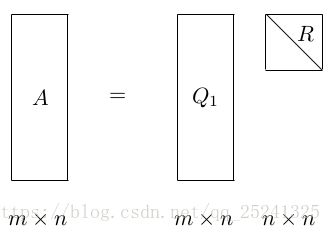
　　QR 分解可以将矩阵分解称为一个标准正交方阵和一个上三角矩阵的积:

QR 分解的计算方式有很多,以下以 Householder 变换为例进行分析。首先我们对基于 Householder 的 QR 分解进行简单的分析,假设 A 为一个 5X4 的矩阵,我们用 X 表示这次变换未变化的元素,用+表示发生变换的元素则有:

  

以此类推,通过四次 Householder 变换就可以将矩阵 A 转换为一个上三角矩阵,且若 A列不相关,则 R 为非奇异矩阵,则有:

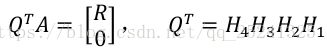那么具体到实际的运算中我们应该怎么通过 Householder 方法计算 QR 分解呢?首先我们先来回顾一下 Householder 变化,对于 Householder 变换我们有以下定义:

然后我们通过一个实际的计算例子来说明 Householder 的 QR 分解变化。案例参考[2]。假设现在我们有以下五个数据:

(-1, 1), (-0.5, 0.5), (0, 0), (0.5, 0.5), (1.2)

并且有满足该数据的线性系统如下所示:

　　首先我们队第一列进行处理:

　　其中的√5为的值,然后我们可以通过公式计算得到

　　然后依次类推,对第二列和第三列进行求解:

至此完成矩阵 A 的 QR 分解。
通过以上方法我们能够求得 Q 和 R 矩阵,那么如何通过他们解决最小二乘问题呢。
对于一个最小二乘问题我们有:

对 A 进行 QR 分解,我们能够得到:

　　在这里我们将拆分为两部分,Q1 代表最开始的 n 行,而 Q2 代表后面与零相乘的剩余部分。

由此进一步我们有:

该结果就为 QR 分解求解线性最小二乘的表达式。

       2.4. 奇异值分解(SVD)

以上形式的最小二乘问题还可以通过 SVD 分解的方法进行求解。对于我们对其中的矩阵 A 进行 SVD 分解有:

由于我们已经假设问题为超定(m>n),因此有:

SVD 的求解方法总结如下,参考[3]. 

三. 齐次方程的最小二乘

之前我们讨论的最小二乘问题其形式都为Ax − b = 0,如果问题形式发生改变,变为Ax = 0,那么这样的最小二乘问题应该如何求解呢?

Ax = 0形式的问题经常出现在重建问题(reconstruction)中。我们期望找到方程Ax = 0中 x 不等于零的解。由于该方程的特殊形式我们会发现对于 x 不等于零的解我们乘上任意的尺度因子 k 使解变为 kx 都不会改变最终结果。因为我们可以将问题转化为求解 x 使得||Ax||值最小并且||x||=1。

现在对矩阵 A 进行 SVD 分解有:

通过 SVD 分解中 D 矩阵的性质我们能够发现,D 为一个对角矩阵,且它的对角线元素呈降序排列。因此方程的解应该为:

该解在最后的位置有一个值为 1 的非零项。依据此结果,再根据方程:

我们可以发现,x 的值就为矩阵 V 的最后一列。

-------------------------------------------------------------------------------------------------------------------------

附:

对于Ax=b, A为一个mXn的矩阵,其结果有以下三种可能性:

• m
• m=n, 如果矩阵A可逆,存在唯一解;
• m>n, 方程个数大于未知数个数.通常情况下方程不会有解,除非b恰好位于矩阵A的列空间中;

 以上内容如有谬误还请告知.

 

参考内容:

[1]. 使用Math.NET求解线性和非线性最小二乘问题

[2]. Least Squares Approximation/Optimization

[3]. Multiple View Geometry in Computer Vision, Appendix 5, Least-squares Minimization

[4]. 机器学习中的矩阵方法03：QR 分解