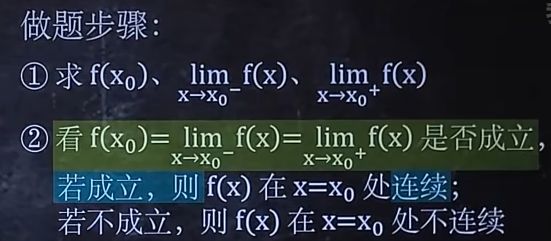高数【连续、间断点】--猴博士爱讲课
第二课《连续、间断点》
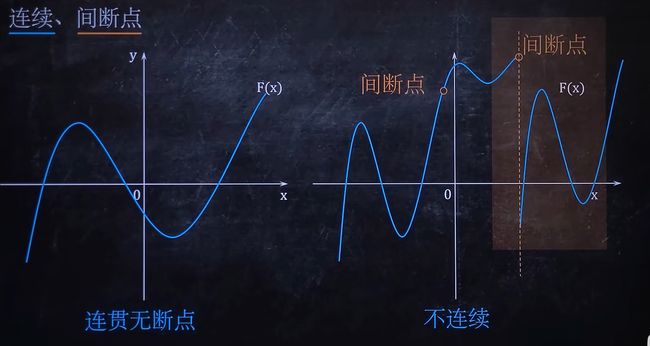
函数连续不连续是要看区间的
1/3 证明f(x)在某点连续
例一:试证明 f ( x ) = { s i n x x , x > 0 1 , x ≤ 0 在 x = 0 处连续 例一:试证明f(x)= \begin{cases} \frac{sinx}{x},x>0 \\ 1,x≤0 \end{cases} 在x=0处连续 例一:试证明f(x)={xsinx,x>01,x≤0在x=0处连续
做题步骤:
① f ( 0 ) = 1 l i m x − > 0 − f ( x ) = l i m x − > 0 − 1 = 1 , l i m x − > 0 + f ( x ) = l i m x − > 0 + s i n x x = l i m x − > 0 + x x = l i m x − > 0 + 1 = 1 ② ∵ f ( 0 ) = l i m x − > 0 − f ( x ) = l i m x − > 0 + f ( x ) 成立 ∴ f ( x ) 在 x = 0 处连续 ①f(0)=1 \\ \mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^-}1=1,\\ \mathop{lim}_{x->0^+}{f(x)}=\mathop{lim}_{x->0^+}{\frac{sinx}{x}}=\mathop{lim}_{x->0^+}{{\frac{x}{x}}}=\mathop{lim}_{x->0^+}1=1\\ ②∵f(0)=\mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^+}{f(x)}成立\\ ∴f(x)在x=0处连续 ①f(0)=1limx−>0−f(x)=limx−>0−1=1,limx−>0+f(x)=limx−>0+xsinx=limx−>0+xx=limx−>0+1=1②∵f(0)=limx−>0−f(x)=limx−>0+f(x)成立∴f(x)在x=0处连续
2/3 已知f(x)在某点连续,求未知数
例二:若函数 f ( x ) = { s i n x a x , x > 0 1 , x ≤ 0 在 x = 0 处连续 , 试求 a 例二:若函数f(x)= \begin{cases} \frac{sinx}{ax},x>0 \\ 1,x≤0 \end{cases} 在x=0处连续,试求a 例二:若函数f(x)={axsinx,x>01,x≤0在x=0处连续,试求a
做题步骤
① f ( 0 ) = 1 l i m x − > 0 − f ( x ) = l i m x − > 0 − 1 = 1 , l i m x − > 0 + f ( x ) = l i m x − > 0 + s i n x a x = l i m x − > 0 + x a x = l i m x − > 0 + 1 a = 1 a ② ∵ f ( x ) 在 x = 0 处连续 , 所以 f ( 0 ) = l i m x − > 0 − f ( x ) = l i m x − > 0 + f ( x ) 成立 ∴ a = 1 ①f(0)=1 \\ \mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^-}1=1,\\ \mathop{lim}_{x->0^+}{f(x)}=\mathop{lim}_{x->0^+}{\frac{sinx}{ax}}=\mathop{lim}_{x->0^+}{{\frac{x}{ax}}}=\mathop{lim}_{x->0^+}\frac{1}{a}=\frac{1}{a}\\ ②∵f(x)在x=0处连续,所以f(0)=\mathop{lim}_{x->0^-}{f(x)}=\mathop{lim}_{x->0^+}{f(x)}成立\\ ∴a=1 ①f(0)=1limx−>0−f(x)=limx−>0−1=1,limx−>0+f(x)=limx−>0+axsinx=limx−>0+axx=limx−>0+a1=a1②∵f(x)在x=0处连续,所以f(0)=limx−>0−f(x)=limx−>0+f(x)成立∴a=1
3/3 间断点
例三:试判断 f ( x ) = { − 1 , x < 1 x , x ≥ 1 的间断点类型 例三:试判断f(x)= \begin{cases} -1,x<1 \\ x,x≥1 \end{cases} 的间断点类型 例三:试判断f(x)={−1,x<1x,x≥1的间断点类型
第一类:左右极限存在,这个点可以定义一个x让fx连续就是可去间断点,如果不可以那就是跳跃间断点。
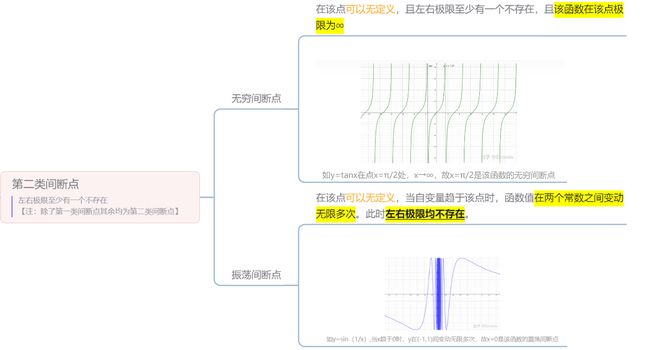
第二类:像是1/x这个函数,x=0就是无穷间断点;fx不为0但是sin或cos后的数为0就是震荡间断点
看看有没有不为∞的值,能使sin、cos后面的式子为∞,且系数不为0。若有,这个点可直接命名为震荡间断点或第二类间断点(震荡)
间断点的概念
若 y = f ( x ) 在 x = x 0 处出现如下三种情况之一,则称 x 0 为 y = f ( x ) 的间断点 : ( 1 ) y = f ( x ) 在点 x 0 处无定义 ( 2 ) y = f ( x ) 在点 x 0 处有定义,但 l i m x − > x 0 f ( x ) 不存在 ( 3 ) y = f ( x ) 在点 x 0 处有定义,但 l i m x − > x 0 f ( x ) 存在,但 l i m x − > x 0 f ( x ) ≠ f ( x 0 ) 据此,我们可以对间断点进行分类 若y=f(x)在x=x_0处出现如下三种情况之一,则称x_0为y=f(x)的间断点:\\ (1)y=f(x)在点x_0处无定义\\ (2)y=f(x)在点x_0处有定义,但\mathop{lim}_{x->x_0}{f(x)}不存在\\ (3)y=f(x)在点x_0处有定义,但\mathop{lim}_{x->x_0}{f(x)}存在,但\mathop{lim}_{x->x_0}{f(x)}≠f(x_0)\\ 据此,我们可以对间断点进行分类 若y=f(x)在x=x0处出现如下三种情况之一,则称x0为y=f(x)的间断点:(1)y=f(x)在点x0处无定义(2)y=f(x)在点x0处有定义,但limx−>x0f(x)不存在(3)y=f(x)在点x0处有定义,但limx−>x0f(x)存在,但limx−>x0f(x)=f(x0)据此,我们可以对间断点进行分类
据此,我们可以对间断点进行分类