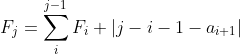和Leo一起做爱线段树的好孩子 数据
Mr_H出了一道信息学竞赛题,就是给n个数排序。输入格式是这样的:试题有若干组数据。每组数据的第一个是一个整数n,表示总共有n个数待排序;接下来n个整数,分别表示这n个待排序的数。
例如:3 4 2 –1 4 1 2 3 4,就表示有两组数据。第一组有3个数 (4,2,-1),第二组有4个数(1,2,3,4)。可是现在 Mr_H做的输入数据出了一些问题。例如:2 1 9 3 2 按理说第一组数 据有2个数(1,9),第二组数据有3个数,可是“3”后面并没有出现三个数,只出现了一个数“2” 而已!
现在Mr_H需要对数据进行修改,改动中“一步”的含义是对文件中的某一个数+1或-1,写个程序,计算最少需要多少步才能将数据改得合法。
线段树优化DP
朴素转移:
我最想的决策单调性明显不对哇QwQ
得线段树优化!
不难发现对于j ![]() 他是不单调的
他是不单调的
但是很明显他是可以查询的
构造线段树查询区间最小值
然后讨论abs的展开所以需要两棵线段树
#include
#include
#include
#include
#include
using namespace std;
#define lc (p<<1)
#define rc (p<<1|1)
const int INF=1e9+7;
const int N=2e6+10;
int A[N];
int B[N];
int F[N];
int m;
struct Node{
int lson,rson,sum;
}T[2][N];
void Build(int Id,int p,int l,int r){
T[Id][p].lson=l;
T[Id][p].rson=r;
T[Id][p].sum=INF;
if(l==r)return;
int mid=(l+r)>>1;
Build(Id,lc,l,mid);
Build(Id,rc,mid+1,r);
}
void PushUp(int Id,int p){
T[Id][p].sum=min(T[Id][lc].sum,T[Id][rc].sum);
}
void Update(int Id,int p,int pos,int val){
if(T[Id][p].lson==pos&&pos==T[Id][p].rson){
T[Id][p].sum=min(T[Id][p].sum,val);
return;
}
int mid=(T[Id][p].lson+T[Id][p].rson)>>1;
if(pos<=mid)Update(Id,lc,pos,val);
else Update(Id,rc,pos,val);
PushUp(Id,p);
}
int Query(int Id,int p,int l,int r){
if(l>r)return INF;
if(l<=T[Id][p].lson&&T[Id][p].rson<=r){
return T[Id][p].sum;
}
int ret=INF;
int mid=(T[Id][p].lson+T[Id][p].rson)>>1;
if(l<=mid)ret=min(ret,Query(Id,lc,l,r));
if(mid< r)ret=min(ret,Query(Id,rc,l,r));
return ret;
}
int main(){
// freopen("test.in","r",stdin);
scanf("%d",&m);
for(int i=1;i<=m;++i)scanf("%d",&A[i]),B[i]=A[i]+i-1;
int len=1e5+1e4+10;
Build(0,1,-len,len);
Build(1,1,-len,len);
Update(0,1,A[1],-A[1]);
Update(1,1,A[1],A[1]);
for(int i=1;i<=m;++i){
// cout<