R语言学习6——数据分析(1)
一、回归分析
线性回归最小二乘法(OSL):lm线性回归分析,要分析的数据集是数据框形式,转化为数据框:as.data.frame( )
常用的查看回归结果的函数:
1.一元线性回归
> fit <- lm(weight~height,data = women)
> fit
Call:
lm(formula = weight ~ height, data = women)
Coefficients:
(Intercept) height
-87.52 3.45
> summary(fit)
Call:
lm(formula = weight ~ height, data = women)
Residuals: //残差
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients: //系数项
Estimate Std. Error t value Pr(>|t|) //H_0:k=0;H_1:k!=0
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 *** //截距项
height 3.45000 0.09114 37.85 1.09e-14 *** //height的系数
--- //weight=3.45*height-87.52
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom //残差标准误差
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903 //R^2衡量拟合质量,取值(0,1)之间,值越大越好
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14 //说明模型是否显著,用p值衡量,越小越显著
2.多元线性回归
衡量模型拟合优劣:AIC赤池信息准则,值越小越好
逐步回归法:逐步删除变量就是向后逐步回归,逐步增加变量就是向前逐步回归。
全子集回归法:检测所有的模型,取最佳。
> fit1 <- lm(Murder~Population+Illiteracy+Income+Frost,data=states)
> fit2 <- lm(Murder~Population+Illiteracy,data=states)
> AIC(fit1,fit2)
df AIC
fit1 6 241.6429
fit2 4 237.6565
> library(MASS)
> states<-as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
> fit <- lm(Murder~Population+Illiteracy+Income+Frost,data=states)
> stepAIC(fit,direction = "backward") //stepAIC逐步回归法
> library(leaps)
> states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
extra argument ‘nbest’ will be disregarded
> leaps<- regsubsets(Murder~Population+Illiteracy+Income+Frost,data=states,nbest=4) //regsubsets全子集回归法3.回归诊断
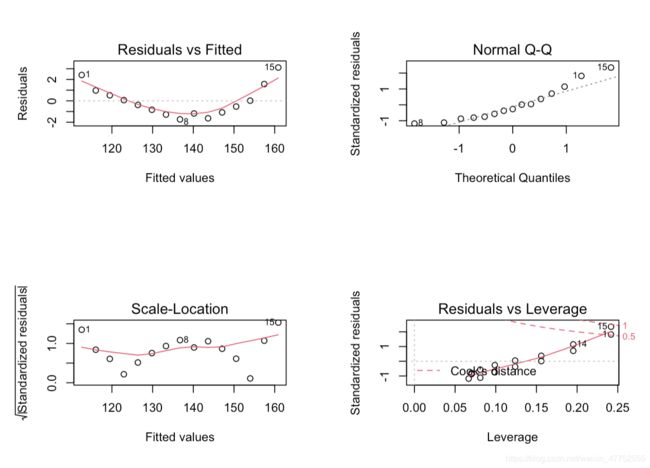
plot(fit)四张图:
残差和拟合图:点是残差的分布,曲线是拟合曲线
Q-Q图:用来描述正态性,如果成正态分布,在图中就是一条直线。
位置与尺寸图:用来描述同方差性,水平线两边的点应该是随机分布的
残差与杠杆图:提供了对单个数据值的观测,可以用来鉴别离群点、高杠杆点和强影响点
二、方差分析(要先转化为因子)
单因素方差分析 双因素方差分析 协方差分析 多元方差分析 多元协方差分析
一般用aov函数分析:
1.单因素方差分析
cholesterol这个数据集是组间的
> fit <- aov(response~trt,data=cholesterol)
> fit
Call:
aov(formula = response ~ trt, data = cholesterol)
Terms:
trt Residuals
Sum of Squares 1351.3690 468.7504
Deg. of Freedom 4 45
Residual standard error: 3.227488
Estimated effects may be unbalanced
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F) //F值越大,说明组间差异越显著;P越小,说明F越可靠
trt 4 1351.4 337.8 32.43 9.82e-13 ***
Residuals 45 468.8 10.4
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 12.单因素协方差分析
litter数据集里面有个协变量gesttime
> fit <- aov(weight~gesttime+dose,data=litter)
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F)
gesttime 1 134.3 134.30 8.049 0.00597 **
dose 3 137.1 45.71 2.739 0.04988 * //可以看出dose对weight是有影响的
Residuals 69 1151.3 16.69
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 13.双因素方差分析
> ToothGrowth$dose <- as.factor(ToothGrowth$dose)
> class(ToothGrowth$dose)
[1] "factor"
> fit <- aov(len~supp*dose,data=ToothGrowth) //supp和dose是有交互的
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 15.572 0.000231 ***
dose 2 2426.4 1213.2 92.000 < 2e-16 ***
supp:dose 2 108.3 54.2 4.107 0.021860 *
Residuals 54 712.1 13.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 14.多元方差分析
> attach(UScereal)
> shelf <- factor(shelf)
> aggregate(cbind(calories,fat,sugars),by=list(shelf),FUN=mean) //aggregate只能处理一个变量,所以先用cbind合成一个数据框
Group.1 calories fat sugars
1 1 119.4774 0.6621338 6.295493
2 2 129.8162 1.3413488 12.507670
3 3 180.1466 1.9449071 10.856821
> fit <- manova(cbind(calories,fat,sugars)~shelf,data=UScereal)
> summary(fit)
Df Pillai approx F num Df den Df Pr(>F)
shelf 1 0.19594 4.955 3 61 0.00383 **
Residuals 63
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> summary.aov(fit) //三组中每种营养成分的测量值都是不同的也就是差异结果是显著的
Response calories :
Df Sum Sq Mean Sq F value Pr(>F)
shelf 1 45313 45313 13.995 0.0003983 ***
Residuals 63 203982 3238
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Response fat :
Df Sum Sq Mean Sq F value Pr(>F)
shelf 1 18.421 18.4214 7.476 0.008108 **
Residuals 63 155.236 2.4641
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Response sugars :
Df Sum Sq Mean Sq F value Pr(>F)
shelf 1 183.34 183.34 5.787 0.01909 *
Residuals 63 1995.87 31.68
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1