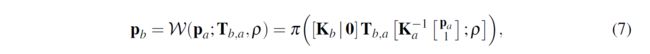深蓝学院-手写VIO作业-第二章

一、基础作业，必做

环境配置说明

a. ROS环境搭建

ros的安装配置参考了下边的博客：

• ROS安装

• ROS安装遇到的问题

找不到rospack包的问题，可以执行下边的命令，将包加入环境变量中（注意路径改成自己的路径）。

source /home/ubuntu/catkin_ws/devel/setup.bash

或者直接写入.bashrc文件

b. Matlab安装

matlab的使用参考文档：

• 这篇主要学会使用查看bag的Topic信息

• 如何执行matlab代码

先执行SCRIPT_allan_matparrallel，再执行SCRIPT_process_results

如果出现缺少Parallel Computing Toolbox，缺少包，直接点击Parallel Computing Toolbox就可以跳转到安装界面j进行安装(执行此步骤前，可先执行下一步，否则可能会出现无法写入的问题)，如果无法跳转，可按此安装说明进行。

安装无法写入的问题：[ubuntu Matlab安装toolbox] 无法写入 /usr/local/MATLAB/R2018b]可参考此篇博客

1、设置IMU 仿真代码中的不同的参数，生成Allen 方差标定曲线。

仿真代码：https://github.com/HeYijia/vio_data_simulation（非ros版本）

allan 方差工具：

​ https://github.com/gaowenliang/imu_utils
​ https://github.com/rpng/kalibr_allan

  课程会提供一个course2_hw_new的压缩包，里边有两个文件夹，其中vio_data_simulation用于产生运动的imu数据，此文件夹下也有用于画图的代码，主要用于下边的a部分。而vio_data_simulation-ros_version文件夹用于产生ros版本的静止的imu仿真数据，主要用于下边的b部分。

course2_hw_new
├── readme.md
├── vio_data_simulation
└── vio_data_simulation-ros_version

a. 对于非ROS：生成运动imu数据

代码调试：

主要执行以下几个步骤（默认用的是欧拉积分）：

1. 编译

   在vio_data_simulation文件夹下，执行如下命令：

   bash build.sh
   

   编译成功：
   

2. 执行bin/data_gen, 生成数据

   将目录切换至bin文件夹下，运行datagen，将会生成很多数据，如下图所示：
   

3. 执行python_tools/draw_trajectory.py ，将会出现如下真实轨迹和imu轨迹的图。
   
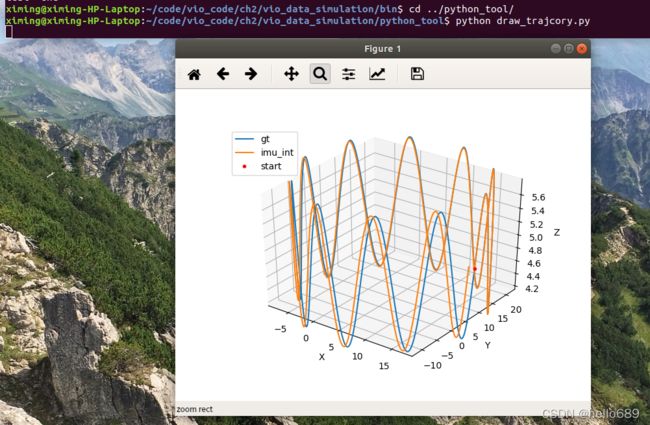
   将欧拉积分换成中值积分的部分将在下边的题2部分进行描述。

代码理解：

代码目录核心代码：

vio_data_simulation
├── bin（存放可执行代码，编译后会生成data_gen可执行文件，用于生成运动imu数据）
│   ├── house_model（里边存放了house模型的关键点，一共23个点对，六维数据（应该是两个点的x,y,z坐标），用于生成点线）
├── main
│   └── gener_alldata.cpp（用于生成所有的数据，最后会产生txt文件，包括imu位姿、相机位姿等数据）
├── python_tool
│   ├── draw_points.py（动态的画出运动的轨迹和房子模型之间的连线，运行的时候需要使用python2执行，否则会报map的错误）
│   ├── draw_trajcory.py（画出真实运动轨迹和imu运动轨迹的线）
│   ├── GeometryLib.py（ 几何变换的一些函数，欧拉角，　旋转矩阵等）
│   └── transformations.py
├── src
│   ├── imu.cpp（包含IMU运动模型部分、测试IMU、添加IMU噪声等函数）
│   ├── param.cpp（camera到世界坐标系的旋转矩阵R）
│   ├── utilities.cpp（包含加载位姿、保存位姿、保存线、保存点等函数）

运行draw_points.py代码，可得下图：

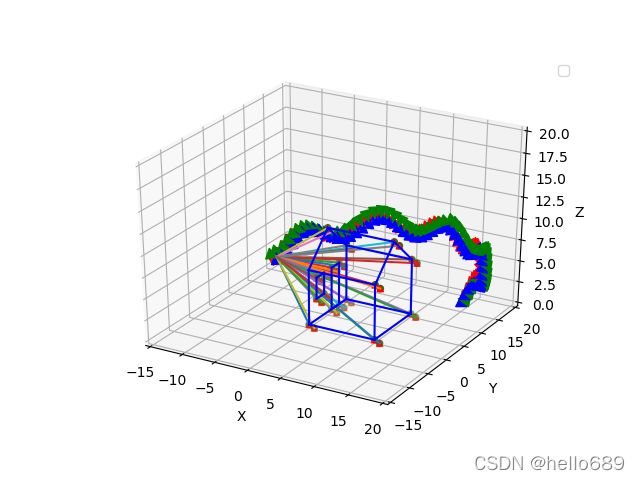
可以看出IMU应该是绕房子做Z轴的正弦运动（此处截图时的视角没有调好，但也能看出是有上下起伏的）。

在imu.cpp代码中，testImu函数读取生成的imu数据并用imu动力学模型对数据进行计算，最后保存imu积分以后的轨迹，其中，使用欧拉积分计算的核心代码如下所示：

 MotionData imupose = imudata[i];

//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
Eigen::Quaterniond dq;
Eigen::Vector3d dtheta_half =  imupose.imu_gyro * dt /2.0;
dq.w() = 1;
dq.x() = dtheta_half.x();
dq.y() = dtheta_half.y();
dq.z() = dtheta_half.z();
dq.normalize();

/// imu 动力学模型 欧拉积分
Eigen::Vector3d acc_w = Qwb * (imupose.imu_acc) + gw;  // aw = Rwb * ( acc_body - acc_bias ) + gw
Qwb = Qwb * dq;
Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
Vw = Vw + acc_w * dt;

此处的代码对应贺博课程中提供的欧拉积分公式（如下图所示的欧拉积分公式），由于g是负值，因此上边的代码里是+gw。

b.对于ROS: 专门生成静止 imu 数据，用于 allan 方差标定

  首先来说一下需要编译哪些工作包，以及该如何编译这些工作包。本题贺一家老师提供了两种方法来完成静止imu数据的allan标定。一种是gaowenliang的imu_utils功能包，一种是使用kalibr_allan功能包来进行标定。这两个功能包可以放在不同的工作空间下来进行编译，也可以放在一个工作空间进行编译。空间太多显得太杂乱（不过这种方式比较简单，也不容易出错），因此我下边将放在一个空间中进行编译。

使用imu_utils完成allan标定
代码调试过程如下：

1. ros下编译

  在imu_utils的的README.md文件中可以看到，编译此功能包需要提前安装一个依赖以及下载一个功能包：

• 安装依赖库

sudo apt-get install libdw-dev

• 下载code_utils，将ros功能包code_utils和imu_utils放入命名为catkin_ws的工作空间中，然后进行catkin_make编译操作。

创建文件夹catkin_ws/src，然后下载code_utils。

git clone https://ghproxy.com/https://github.com/gaowenliang/code_utils

注：这里的编译可能会有三四个需要注意的地方，推荐先看一下这篇博客，做出相应修改，可以提前避坑。

成功编译code_utils功能包，截图如下：

2. 执行, 生成 imu.bag

• 将课程提供一个vio_data_simulation-ros_version文件夹放入src文件夹下，执行catkin_make命令进行编译。vio_data_simulation_node就是用来生成数据的。
  

• 将功能包名添加到当前Ternimal的环境变量中，也可以直接写入环境变量的配置文件。注意下边的路径改成你自己的路径。

   source /home/ximing/code/vio_code/ch2/catkin_ws/devel/setup.bash
  

• 运行数据生成node，生成imu.bag数据，路径是/home/ximing/imu.bag

   rosrun vio_data_simulation vio_data_simulation_node
  

  

3. rosbag play -r 500 imgimu_utils.bag 回放

   执行rosbag info /home/ximing/imu.bag查看imu.bag的信息，可以看出topic信息是imu：
   

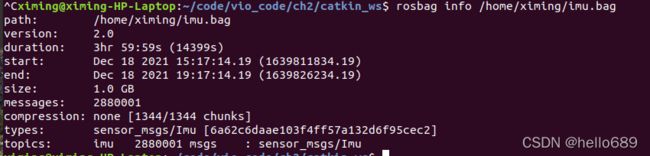
   这里需要在imu_utils/launch添加一个imu.launch文件:

   运行标定工具imu_utils，用imu_utils进行接收和分析，执行如下命令：

   source /home/ximing/code/vio_code/ch2/catkin_ws/devel/setup.bash
   roslaunch imu_utils imu.launch
   

   另起一个终端执行如下命令：

   source /home/ximing/code/vio_code/ch2/catkin_ws/devel/setup.bash
   rosbag play -r 500 /home/ximing/imu.bag
   

   运行过程如下图所示：
   

4. 用imu_utils进行接收和分析

   执行上边3的两个命令之后，会在analysis_imu_data文件夹下生成17个txt文件。这些文件就是测出来的误差。

5. 用imu_utils下的scripts/下的matlab 脚本画allan曲线
     修改matlab脚本文件draw_allan.m代码，将路径改到创建的analysis_imu_data下，修改txt文件路径，运行该程序得到如下allan曲线，此图像为陀螺仪和加速度计的allan曲线，其中o是陀螺仪的allan曲线，线型的是加速度计的allan曲线:
   

代码理解：

根据交流群里Krasjet的提示，我对imu_utils和kalibar_allan这两个包有了更深的理解。其实都是来画allan曲线的，那么为什么要画这个曲线呢？上课的时候贺博也说了，IMU中的误差分为确定性误差和随机误差，确定性误差主要有bias和scale，这是可以计算的固定的值（通过六面法来标定）；而随机误差有高斯白噪声、Bias随机游走，这些误差通常是一个连续的变化的，因此用allan方差法进行标定，得到方差随时间变化的曲线。

  在imu数据生成的代码文件中，也就是vio_data_simulation-ros_version/src/param.h代码中，有关于陀螺仪和加速度计的白噪声和随机游走的参数设置，如下所示：

// noise
double gyro_noise_sigma = 0.015;    // rad/s * 1/sqrt(hz)
double acc_noise_sigma = 0.019;      //　m/(s^2) * 1/sqrt(hz)
// bias
double gyro_bias_sigma = 0.00005;
double acc_bias_sigma = 0.0005;

在imu_utils的readme文件中，有yaml元素对应的参数名：

Parameter	YAML element	Symbol	Units
Gyroscope “white noise”	gyr_n
Accelerometer “white noise”	acc_n
Gyroscope “bias Instability”	gyr_w
Accelerometer “bias Instability”	acc_w

而在生成的yaml文件中，有对应的陀螺仪和加速度计的白噪声和随机游走噪声。

%YAML:1.0
---
type: IMU
name: stop_imu
Gyr:
   unit: " rad/s"
   avg-axis:
      gyr_n: 2.0884360791447706e-01
      gyr_w: 9.0695665742635391e-04
   x-axis:
      gyr_n: 2.1186773934825751e-01
      gyr_w: 1.0139460114514782e-03
   y-axis:
      gyr_n: 2.0601878667075832e-01
      gyr_w: 7.4302335795599340e-04
   z-axis:
      gyr_n: 2.0864429772441534e-01
      gyr_w: 9.6390060287159050e-04
Acc:
   unit: " m/s^2"
   avg-axis:
      acc_n: 2.7062854995667557e-01
      acc_w: 3.7668581694479870e-03
   x-axis:
      acc_n: 2.7140180391239443e-01
      acc_w: 3.4131924184579365e-03
   y-axis:
      acc_n: 2.7115925797881452e-01
      acc_w: 3.7894516281332222e-03
   z-axis:
      acc_n: 2.6932458797881770e-01
      acc_w: 4.0979304617528032e-03

此时，需要将标定结果转化为连续时间的结果，贺博课程中讲了如何进行转换。也可以参考博客说的也很清楚。下边的计算我是使用手机人工计算的：

$$\begin{gathered} accelerometernoise=2.7062854995667557e-01\ast \frac{1}{\sqrt{200}}\approx 0.019136328 \\ accelerometerbiasinstability=3.7668581694479870e-03\ast \sqrt{200} \\ gyroscopenoise=2.0884360791447706e-01\ast \frac{1}{\sqrt{200}}\approx 0.01476747313 \\ gyroscopebiasinstability=9.0695665742635391e-04\ast \sqrt{200} \end{gathered}$$
最后可以看出计算得到的白噪声的参数与提前设置的参数几乎一样，另外bias instability应该不是随机游走参数。

使用 kalibr_allan 完成 allan 标定（推荐）

1. ros下编译

   将kalibr_allan功能包放入src文件下，回退至工作空间，进行catkin_make编译

2. 执行, 生成 imu.bag

   此步骤可省略，在使用imu_utils时已经生成过了。

3. 用kalibr_allan的bagconver把bag转成 mat文件, 见readme

   执行如下命令：

   rosrun bagconvert bagconvert /home/ximing/imu.bag imu
   

   

4. 用kalibr_allan的m脚本对mat文件进行分析, (需修改m文件中的mat文件路径)

   使用matlab软件，运行SCRIPT_allan_matparallel.m脚本文件

   

   运行结束后，在kalibr_allan/data文件夹下生成一个.mat文件。

5. 用kalibr_allan的m脚本画allan曲线, (需修改m文件中的result文件路径)

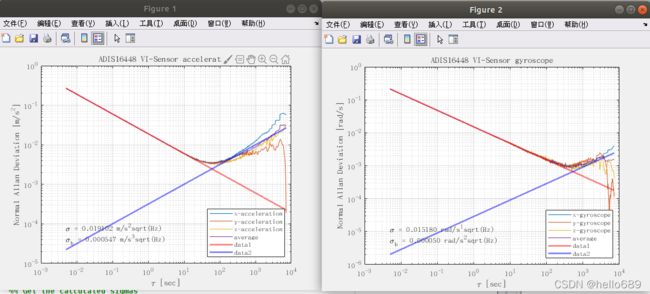
   修改mat文件路径为kalibr_allan/data文件夹下的.mat文件，运行SCRIPT_process_results.m脚本文件，会得到加速度计和陀螺仪的Allan方差标定曲线

   其中，误差结果为：

   accelerometer_noise_density = 0.01910187
   accelerometer_random_walk   = 0.00054711
   gyroscope_noise_density     = 0.01518023
   gyroscope_random_walk       = 0.00004984
   

   加速度计和陀螺仪的Allan方差标定曲线如下图所示：
   
   可以看出得到的方差参数与parm.h中设定的参数很接近。

2、将IMU仿真代码中的欧拉积分替换成中值积分。

中值积分和欧拉积分的思想：

  欧拉法，即两个相邻时刻 k 到 k+1 的位姿是用第 k 时刻的测量值 a, ω 来计算，中值法即两个相邻时刻 k 到 k+1 的位姿是用两个时刻的测量值 a, ω 的平均值来计算。这里借用贺博的两个手绘图，画图更好说明、理解一些：

代码修改的核心部分：

 /// imu 动力学模型 中值积分
 MotionData imupose = imudata[i];
 MotionData imuposeK = imudata[i-1];

//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
Eigen::Quaterniond dq;
Eigen::Vector3d dtheta_half =  ((imupose.imu_gyro + imuposeK.imu_gyro)/2.0) * dt /2.0;
dq.w() = 1;
dq.x() = dtheta_half.x();
dq.y() = dtheta_half.y();
dq.z() = dtheta_half.z();
dq.normalize();

Eigen::Vector3d acc_w = (Qwb * (imupose.imu_acc) + gw + Qwb * (imuposeK.imu_acc) + gw)/2.0;  // aw = Rwb * ( acc_body - acc_bias ) + gw
Qwb = Qwb * dq;
Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
Vw = Vw + acc_w * dt;

（避坑提示，如果是在上边欧拉积分的基础上修改的代码，在重新编译的时候，先手动的删除build文件夹下的文件，再重新编译，否则可能出错。）

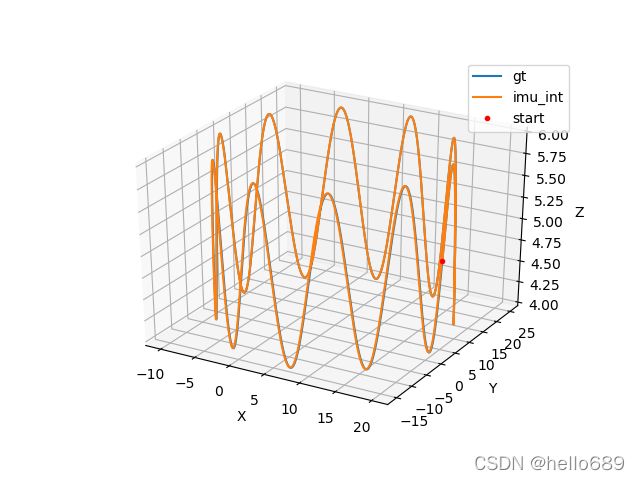
运行结果如下图所示，黄线（轨迹）和蓝线（实际运动轨迹）高度重合，与欧拉积分相比，积分结果更精确。

二、提升作业，选做

1、阅读从已有轨迹生成imu 数据的论文，撰写总结推导：

文献：2013 年 BMVC, Steven Lovegrove ,Spline Fusion: A continuous-time representation for visual-inertial fusion with application to rolling shutter cameras.

本题主要是做一个总结，以及轨迹生成B样条、B样条产生加速度的推导。

总结：这篇文章描述了一种使用低成本传感器(如卷帘快门CMOS相机和MEMS IMUs)实现稳健SLAM的方法。本文使用了一个连续时间的模型来描述摄像机的轨迹，融合来自许多不同步的高速率传感器的信息，同时限制状态大小。我们明确地模拟了相机的滚动快门(如下图所示)，并且可以在惯性测量中产生误差。该模型不仅限于视觉惯性SLAM，还可以简化其他传感器的集成，如旋转SICK激光测距仪。

  该方法的另一个重要应用是对非同步的多传感器进行最小二乘标定。通过在连续时间模型中定义所有传感器的姿态，可以联合估计所有传感器的参数，包括那些测量时间导数的参数，如陀螺仪和加速度计。给定近似的初始传感器配置，我们可以找到非常精确的传感器参数。

  然后作者介绍了一些之前研究者们提出的方法，而这些方法都使用离散时间状态表示。另外也有少许研究者的方法跟本文的相近，都使用了连续表示。不过他们的方法是基于飞行器轨迹的样条表示。

本文的核心方法是连续的轨迹表示，这种表示是建立在以下几点基础上的：

• 本地控制，允许系统在线和批量运行；
• 具有$C^2$连续性，使我们能够预测IMU的测量；
• 具有最小扭矩轨迹的良好近似。B样条是一个比较好用的用于表示连续轨迹的方法。但在处理3D旋转时就不那么容易应用了，比如插值；
• 是可参数化且无奇异点的刚体运动。

为满足以上性质，本文选择累积B样条插值法，这种方法允许在样条曲线上的任意一点计算解析时间倒数。可以很容易地合成加速度计和陀螺仪的测量值，反过来利用他们对观测到的测量值形成直接误差。

用累积基函数表示b样条

k-1次B样条曲线的标准基函数表示为：

其中$p_i\in {\mathbb{R}}^N$是$t_i$时刻的控制点$i\in [0,...,n]$，$B_{i,k}(t)$是basis functions，公式1可以推导成如下形式：

通过控制点进行对数映射代替对控制点做差值，连乘的指数映射代替求和，重写上式轨迹描述，得到下边的公式：

累积三次B样条

在本文中，我们着重讨论了累积三次b样条的特殊情况(k=4时)，我们假设控制点分布在均匀的一段时间内($\Delta t$)。在三次b样条中，四个控制点影响在t时刻的样条曲线的值。我们将这些控制点定义为集合$[t_{i-1},t_i,t_{i+1],t_{i+2}}]$。我们可以用统一的时间表示法$s(t)=(t-t_0)\Delta t$进一步简化表示。利用此时间公式和基于矩阵表示的De Boor - Cox公式，我们可以写出累加基的矩阵表示形式:

样条轨迹中的姿态现在可以定义为:

则位姿对于时间的一阶二阶导数如下：

通过B样条产生加速度

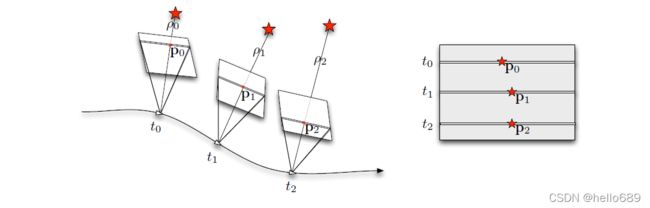
我们从沿着我们的样条的第一个观察姿势，使用逆深度参数化系统中的地标。已经证明，逆深度表示允许对无穷远处的点进行简单的处理，极大地简化了单目特征的初始化。我们可以将在投影相机帧中观测到的逆深度点转换为图像坐标，其对应的图像位置$p_b$表示如下：

累积b样条参数化允许我们计算解析时间导数，在上一部分有说明，这使得我们可以简单地合成加速度计和陀螺仪的测量值，我们可以反过来用它们来形成观测值的误差。

最小化损失函数

给定我们的视觉和惯性数据生成模型，我们可以通过最小化由测量和预测观测的差异形成的目标函数来批量或通过一个窗口来求解样条和相机参数。通过使用连续时间公式，重投影误差和惯性误差可以被统一处理，并由设备规格或校准计算出的各自的信息矩阵S加权。最小化公式如下：

代码地址：https://gitee.com/ximing689/vio-learning.git