2020年MathorCup高校数学建模挑战赛—大数据竞赛A题移动通信基站流量预测求解全过程文档及程序

2020年MathorCup高校数学建模挑战赛—大数据竞赛

A题 移动通信基站流量预测

原题再现：

  随着移动通信技术的发展，4G、5G 给人们带来了极大便利。移动互联网的飞速发展，使得移动流量呈现爆炸式增长，从而基站的流量负荷问题变得越来越重要。一方面，在流量高峰期，大量基站呈现出负荷超过容量的问题，使得即使信号条件很好，网络速度也非常的慢，给用户带来非常差的体验。为了改善这个问题，需要给基站增加载频的数量来扩容，使基站可以承载更多的流量；另一方面，由于基站潮汐现象，使得在某些时段，用户数量会大幅降低。如图 1 所示，是某基站下行流量随时间变化的曲线。

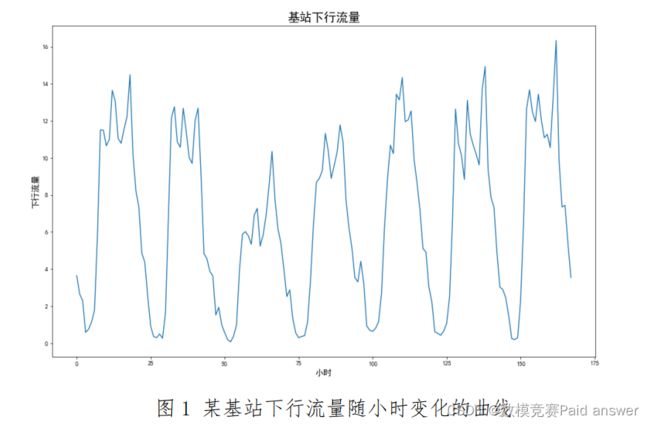
  在基站低流量时段，如果仍然按照高容量时段的载频数量来运行基站配置，会极大的浪费资源和能量。特别是现在每个城市的基站数量巨大，而且随着 5G 的不断部署，基站数量还会大幅增加。同时，每个基站的流量高峰和低谷的时段各不相同。如果所有基站都按照高容量时段来配置运行载频，则网络的能量消耗是非常巨大的。因此，需要根据流量的变化，计算需要的载频数量，从而可以在不同时段打开或者关闭部分载频使得基站既可以满足对用户的服务，又可以尽可能低的消耗能量和资源。
  由于基站数量巨大，无法通过人工实时关注每个基站的流量变化，需要给每个基站设置根据时段自动开关载频的程序。这样就需要知道一段时间内基站流量关于时段的变化值，特别是基站在每个小时的上下行流量值。从而可以知道基站在每个时段需要的载频的数量，进而设置一定时间内基站载频自动开关的程序。
  另外，无论基站流量随时段怎么波动，从长期来看，大部分基站的整体流量是呈逐渐增加趋势的。当整体流量增加到一定程度时，这种动态开关载频的方式已经无法满足基站在流量峰值时候的需求了，因此需要做物理扩容，新建扇区或者新建基站。由于物理扩容需要涉及采购、费用、总体布局等问题，因此规划需要的时间非常长，所以需要提早预估出基站需要物理扩容的时间，从而可以更早的进行规划和设计。
  基于以上背景，请你们的团队根据附件给出的数据，通过数据分析与建模的方法帮助移动通信运营商解决下面的问题：
  问题 1：对小区(基站的每个扇区)的上行和下行流量随时间的变化进行建模，并用附件 1 中的“训练数据”(部分小区 2018 年 3 月 1 日至 4 月19 日的小时级流量数据)训练模型，给出各个小区小时级上行和下行流量的预测模型，预测这些小区后面一周(4 月 20 日至 4 月 26 日)的小时级流量变化，并将附件 2“短期验证选择的小区数据集”中涉及的小区数据填充完成，填充结果提交到竞赛网站平台，请勿改变附件 2 中数据的格式及小区 ID 编号顺序。
  问题 2：预测小区上下行流量的长期变化趋势，给出每个小区长期流量预测模型，并对附件 3“长期验证选择的小区数据集”中涉及的小区，预测其在 2020 年 11 月 1 日至 11 月 25 日每天的总的上行和下行流量，填充该数据表，并提交到竞赛网站平台，请勿改变附件 3 中数据的格式及小区 ID编号顺序。
  问题 3：依据给出的样本数据集，你们觉得还有哪些问题值得研究，并给出你们的思路？

整体求解过程概述(摘要)

  随着移动通信技术的发展，基站作为移动通信的基础设施，其承载网络流量持续增加．本文建立基于流量时间序列特征的聚类模型对小区进行分类，基于基站智能开关载频算法对基站载频的流量阈值进行研究．该问题的研究能智能调节基站载频数，降低基站节能减排效率，符合中国能源结构的发展趋势．
  针对问题一，主要需要对小区进行分类．本文建立了二级聚类模型，首先我们对各小区流量的消耗量进行分析，利用消耗量的评级对小区进行第一级聚类划分．对附件一中的数据预处理，选取 6 个与小区流量消耗有关的特征：“小区日均上行业务量GB”、“小区上行业务量大于 1GB 的天数”、“小区上行业务量小于 0.2GB”、“小区日均值下行业务量”、“小区下行业务量大于 1GB 的天数”、“小区下行业务量小于 0.2GB的天数”．基于流量消耗特征对小区进行一级聚类，将小区划分为“活跃类”、“较活跃类”、“较平淡类”、“平淡类”．接着，选取 12 个有关流量时间序列的特征：“上行昼夜差均值”、“上行周差均值”、“上行近似熵”、“上行样本熵”、“上行白天消耗流量序列方差”以及对应的下行流量数据特征．基于时间序列特征对小区进行二级聚类，最终得到 16 个小区类型，并对每一类小区特点进行说明．
  针对问题二，需要给出基站载频的流量阈值的设置策略和具体结果．我们对基站能耗和用户服务这两个指标进行研究，基站能耗主要从基站业务负载和基站静态能耗上考虑，基站业务负载为小区用户使用的流量总和，基站静态能耗为维持基站运行的最小功耗．根据小区的业务量与基站分配的载频容量差值，确立了一种基站的动态分配载频机制，使基站分配给小区的载频数既能满足用户流量需求，也使基站能耗最低．基于基站能耗和服务质量这两个指标，采用线性加权法，对蜂窝网络整体综合评价，选择适当的权重，使得达到基站能耗和用户服务质量两者达到最优值．由于数据的限制，我们仿真计算时将模型简化为单基站多小区型．提取 186，221，546 等小区一周的数据，通过仿真得到载频阈值，最终确定了该基站开关流量阈值 2.485GB.
  最后，本文对第二问的模型进行稳定性检验，对不减函数进行多种函数的取样测试．结果得到在选取不同函数时，网络整体的评价趋势与得分都较为相似，由此可以得出该模型具有一定的稳定性．另外，我们对模型进行了优、缺点评价．最后经过分析检验，本文的模型具有合理性和一定的现实意义．

模型假设：

  1、假设所调查的有关基站的数据都比较准确;
  2、假设基站使用宏基站能耗模型；
  3、假设小区所属基站不会因为人工或自然原因突然损坏；
  4、假设附件中所给小区覆盖地区的流量使用不考虑新建基站的影响；
  5、假设网络模型为蜂窝网络模型．

问题分析：

问题一的分析

  问题一主要需要我们提取附件 1 中小区上行和下行流量的时间序列数据的特征，对小区进行分类．在小区的分类中并不依赖于其本身的特征属性，而是主要参考覆盖范围内的主导场景．不同基站由于其覆盖范围内用户、使用业务的差异性，其流量模式也存在极大的差异．比如，在工作区域，小区流量高峰一般出现在早上 7-11 点和下午 13-17 点处于上班时间；在餐饮区域，基站流量高峰一般出现在中午和晚上吃饭时间．但是，由于小区覆盖范围内场景的混合性以及不同场景的相似性，这种划分并不具备代表性．
  对于第一问，我们提出了一种基于时间序列特征的聚类方式，从时间序列的分布、熵、稳定性、尺度变化提取时间序列的特征形成时间序列特征向量．
  为了对小区进行更细一步的划分，我们先基于能量消耗模型对小区进行第一层聚类，选取“小区日均上行业务量 GB”、“小区上行业务量大于 1GB 的天数”、“小区上行业务量小于 0.2GB”、“小区日均值下行业务量”、“小区下行业务量大于 1GB 的天数”、“小区下行业务量小于 0.2GB 的天数”作为一级聚类特征．根据流量使用量，利用聚类算法，将小区流量使用划分活跃类、较活跃类、较平淡类、平淡类．基于第一层聚类后的小区，我们再使用时间序列特征的聚类方式对小区进行第二层聚类，选取“上行昼夜差均值”、“上行周差均值”、“上行近似熵”、“上行样本熵”、“上行白天消耗流量序列方差”、“下行夜晚消耗 1 流量序列方差”、“下行昼夜差均值”、“下行周差均值”、“下行近似熵”、“下行样本熵”、“下行白天消耗流量序列方差”、“下行夜晚消耗流量序列方差”作为二级聚类特征向量，利用聚类算法，对小区进行更细一步的划分．并将每一类的小区绘制出一周的流量趋势图，说明该类小区的流量趋势特点．
  关于问题一的具体思路图如下：

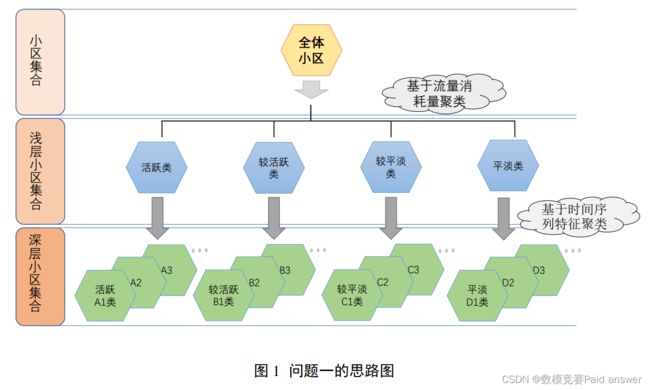
问题二的分析

  问题二主要需要我们对基站阈值的设置进行研究，基站的能源消耗主要来着小区的流量使用．而流量本身存在“潮汐现象”，如果基站以高容量的载频来运行，则对基站能耗是一个很大问题；如果基站关闭一些载频数来降低能耗，在一定程度上，使得用户的服务质量下降．基站智能开关载频算法是我们解决问题的关键，寻找既能使用户达到满足状态，确保用户的服务质量，又能使基站开启较低的载频数，使基站的能耗消耗较低．
  通过蜂窝网络结构模型，建立小区覆盖下的用户与基站的联系．基站能耗从基站业务负载和基站静态能耗上考虑，基站的业务负载为该基站下所有小区用户所需要满足的流量总和，基站静态能耗是指基站没有传输数据时，维持基站运行的最小功耗．小区的流量使用一般会有时间性，不同的时间下用户使用流量的需求不同．对此，我们确立了基站的动态分配载频机制．如果某一时刻小区的业务量高于基站分配小区的载频容量，那么说明基站需要分配格外的载频以满足需求；如果小区的业务量等于基站分配小区的载频容量，那么说明基站与小区业务量之间达到了平衡，无需额外的操作；如果小区的业务量小于基站分配的载频容量，说明基站可以关闭一部分的载频数．一方面除了考虑基站能耗，另一方面还要考虑用户的服务质量，指需要为用户提供更好的服务能力．
  基于基站能耗和用户服务这两个指标，对蜂窝网络整体综合评价，采用线性加权法，作为目标函数．基于需求，改变权重系数来改变模型的适应性．基站根据小区业务量的变化，分配小区最合适的载频数，使得既能满足用户的流量需求，也能使基站能耗达到最低，使整个蜂窝网络能耗达到最低．

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分Python程序如下:

used_feat = ['HOUR','DAY','NAME','MON']
train_x = train[used_feat]
train_y = train['LABEL1']
test_x = test1[used_feat]
print(train_x.shape, test_x.shape)

# -----------------------------------------------
scores = []

params = {'learning_rate': 0.1, 
        'boosting_type': 'gbdt', 
        'objective': 'regression',
        'metric': 'rmse',
        'min_child_samples': 46, 
        'min_child_weight': 0.01,
        'feature_fraction': 0.8, 
        'bagging_fraction': 0.8, 
        'bagging_freq': 2, 
        'num_leaves': 16, 
        'max_depth': 5, 
        'n_jobs': -1, 
        'seed': 2019, 
        'verbosity': -1, 
       }



oof_train = np.zeros(len(train_x))
preds = np.zeros(len(test_x))
folds = 5
seeds = [2048, 1997]
for seed in seeds: 
    kfold = KFold(n_splits=folds, shuffle=True, random_state=seed)
    for fold, (trn_idx, val_idx) in enumerate(kfold.split(train_x, train_y)):
        print('fold ', fold + 1)
        x_trn, y_trn, x_val, y_val = train_x.iloc[trn_idx], train_y.iloc[trn_idx], train_x.iloc[val_idx], train_y.iloc[val_idx]
        train_set = lgb.Dataset(x_trn, y_trn)
        val_set = lgb.Dataset(x_val, y_val)

        model = lgb.train(params, train_set, num_boost_round=5000,
                          valid_sets=(train_set, val_set), early_stopping_rounds=25,
                          verbose_eval=50)
        oof_train[val_idx] += model.predict(x_val) / len(seeds)
        preds += model.predict(test_x) / folds / len(seeds)
        del x_trn, y_trn, x_val, y_val, model, train_set, val_set
        gc.collect()
    
    mse = (mean_squared_error(oof_train, train['LABEL1']))
    
    print('-'*120)
    print('rmse ', round(mse, 5))


test1['LABEL1'] = preds

train_x = train[used_feat]
train_y = train['LABEL2']
test_x = test1[used_feat]
print(train_x.shape, test_x.shape)

# -----------------------------------------------
scores = []

params = {'learning_rate': 0.1, 
        'boosting_type': 'gbdt', 
        'objective': 'regression',
        'metric': 'rmse',
        'min_child_samples': 46, 
        'min_child_weight': 0.01,
        'feature_fraction': 0.8, 
        'bagging_fraction': 0.8, 
        'bagging_freq': 2, 
        'num_leaves': 16, 
        'max_depth': 5, 
        'n_jobs': -1, 
        'seed': 2019, 
        'verbosity': -1, 
       }



oof_train = np.zeros(len(train_x))
preds = np.zeros(len(test_x))
folds = 5
seeds = [2048, 1997]
for seed in seeds: 
    kfold = KFold(n_splits=folds, shuffle=True, random_state=seed)
    for fold, (trn_idx, val_idx) in enumerate(kfold.split(train_x, train_y)):
        print('fold ', fold + 1)
        x_trn, y_trn, x_val, y_val = train_x.iloc[trn_idx], train_y.iloc[trn_idx], train_x.iloc[val_idx], train_y.iloc[val_idx]
        train_set = lgb.Dataset(x_trn, y_trn)
        val_set = lgb.Dataset(x_val, y_val)

        model = lgb.train(params, train_set, num_boost_round=5000,
                          valid_sets=(train_set, val_set), early_stopping_rounds=25,
                          verbose_eval=50)
        oof_train[val_idx] += model.predict(x_val) / len(seeds)
        preds += model.predict(test_x) / folds / len(seeds)
        del x_trn, y_trn, x_val, y_val, model, train_set, val_set
        gc.collect()
    
    mse = (mean_squared_error(oof_train, train['LABEL2']))
    
    print('-'*120)
    print('rmse ', round(mse, 5))


test1['LABEL2'] = preds

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可