变换(二维与三维,模型,视图,投影)——计算机图形学
要点速览
-
缩放(Scale): [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} s_x & 0\\ 0 & s_y \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} [x′y′]=[sx00sy][xy]
-
反射(Reflection): [ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] ( 关 于 y 轴 ) [ x ′ y ′ ] = [ 1 0 0 − 1 ] [ x y ] ( 关 于 x 轴 ) \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} -1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(关于y轴) \quad\quad \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(关于x轴) [x′y′]=[−1001][xy](关于y轴)[x′y′]=[100−1][xy](关于x轴)
-
切变(Shear): [ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] ( x 方 向 上 的 切 变 ) [ x ′ y ′ ] = [ 1 0 a 1 ] [ x y ] ( y 方 向 上 的 切 变 ) \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(x方向上的切变) \quad\quad \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 1 & 0\\ a & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(y方向上的切变) [x′y′]=[10a1][xy](x方向上的切变)[x′y′]=[1a01][xy](y方向上的切变)
-
旋转(Rotate): R θ = [ cos θ − sin θ sin θ cos θ ] \mathbf{R}_{\theta}= \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} Rθ=[cosθsinθ−sinθcosθ]
-
平移(Translation): ( x ′ y ′ w ′ ) = ( 1 0 t x 0 1 t y 0 0 1 ) ⋅ ( x y 1 ) \begin{pmatrix} {x}'\\ {y}'\\ {w}' \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} ⎝⎛x′y′w′⎠⎞=⎝⎛100010txty1⎠⎞⋅⎝⎛xy1⎠⎞
-
齐次坐标:2D 点: ( x , y , 1 ) T (x,y,1)^{T} (x,y,1)T,2D 向量: ( x , y , 0 ) T (x,y,0)^{T} (x,y,0)T 。 w ≠ 0 w \neq 0 w=0 时每一项都除以 w w w,就是 2D 点。
-
仿射变换(Affine Transformation)= (先)线性变换 + (再)平移: ( x ′ y ′ 1 ) = ( a b t x c d t y 0 0 1 ) ⋅ ( x y 1 ) \begin{pmatrix} {x}'\\ {y}'\\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} ⎝⎛x′y′1⎠⎞=⎝⎛ac0bd0txty1⎠⎞⋅⎝⎛xy1⎠⎞
-
变换的顺序不能调换,从右往左写(左乘)。
-
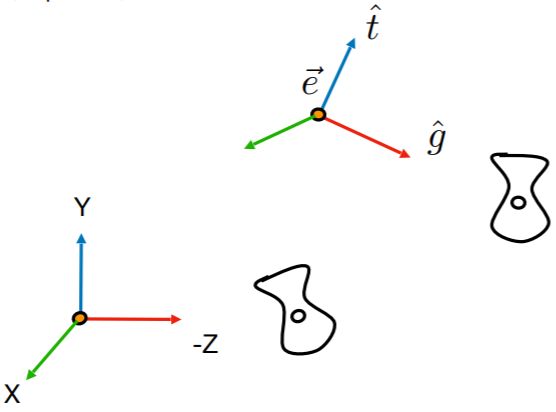
视图变换(View / Camera transformation):Camera is at the origin, up at Y Y Y, look at − Z -Z −Z,让物体跟着相机走。
- 相机的位置 e ⃗ \vec{e} e,观察方向 g ^ \hat{g} g^,向上方向 t ^ \hat{t} t^ (假定垂直于观察方向)
- M v i e w = R v i e w T v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] [ 1 0 0 − x e 0 1 0 − y e 0 0 1 − z e 0 0 0 1 ] M_{view}=R_{view}T_{view} =\begin{bmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{bmatrix} Mview=RviewTview=⎣⎢⎢⎡xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−xe−ye−ze1⎦⎥⎥⎤
-
正交投影(Orthographic projection):长方体 [ l , r ] × [ b , t ] × [ f , n ] \left [ l,r \right ]\times \left [ b,t \right ]\times \left [ f,n \right ] [l,r]×[b,t]×[f,n] map(映射) 到 标准视体 [ − 1 , 1 ] 3 \left [ -1,1 \right ]^{3} [−1,1]3 (注意: n > f n > f n>f),先平移再缩放
- M o r t h o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 l + r l − r 0 2 t − b 0 b + t b − t 0 0 2 n − f f + n f − n 0 0 0 1 ] M_{ortho}=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & \frac{l + r}{l -r}\\ 0 & \frac{2}{t-b} & 0 & \frac{b + t}{b -t}\\ 0 & 0 & \frac{2}{n-f} & \frac{f + n}{f-n}\\ 0 & 0 & 0 & 1 \end{bmatrix} Mortho=⎣⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎤=⎣⎢⎢⎡r−l20000t−b20000n−f20l−rl+rb−tb+tf−nf+n1⎦⎥⎥⎤
-
透视投影(Perspective projection):近大远小,平行线不再平行。
- M p e r s p = M o r t h o M p e r s p → o r t h o = M o r t h o ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) = ( 2 n r − l 0 l + r l − r 0 0 2 n t − b b + t b − t 0 0 0 n + f n − f 2 f n f − n 0 0 1 0 ) M_{persp}=M_{ortho} M_{persp \rightarrow ortho}=M_{ortho} \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix}= \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0 \end{pmatrix} Mpersp=MorthoMpersp→ortho=Mortho⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞=⎝⎜⎜⎛r−l2n0000t−b2n00l−rl+rb−tb+tn−fn+f100f−n2fn0⎠⎟⎟⎞
文章目录
- 要点速览
- 2D 变换
-
- 缩放(Scale)
- 反射(Reflection)
- 切变(Shear)
- 旋转(Rotate)
- 齐次坐标(Homogenous Coordinates)
-
- 齐次坐标表示法
- 平移(Translation)
- 仿射变换(Affine Transformation)
- 变换与顺序
- 3D 变换
-
- 3D 点、向量的齐次坐标表示
- 三维空间中的旋转
-
- 罗德里格斯旋转公式(Rodrigues’ Rotation Formula)
- Viewing transformation
-
- 视图变换(View / Camera transformation)
- 投影变换(Projection transformation)
-
- 正交投影(Orthographic projection)
- 透视投影(Perspective projection)
2D 变换
缩放(Scale)
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} s_x & 0\\ 0 & s_y \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} [x′y′]=[sx00sy][xy]
【例】对应下图: [ x ′ y ′ ] = [ 0.5 0 0 1.5 ] [ x y ] \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 0.5 & 0\\ 0 & 1.5 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} [x′y′]=[0.5001.5][xy]

反射(Reflection)
[ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] ( 关 于 y 轴 ) \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} -1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(关于y轴) [x′y′]=[−1001][xy](关于y轴)
[ x ′ y ′ ] = [ 1 0 0 − 1 ] [ x y ] ( 关 于 x 轴 ) \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(关于x轴) [x′y′]=[100−1][xy](关于x轴)
如果对角线的两个元素都是 − 1 -1 −1(即 [ − 1 0 0 − 1 ] \begin{bmatrix}-1 & 0\\ 0 & -1\end{bmatrix} [−100−1]),那就相当于是一个(绕原点) π \pi π 弧度的旋转。这种旋转也可以称为“通过原点的反射”。
切变(Shear)
[ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] ( x 方 向 上 的 切 变 ) \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(x方向上的切变) [x′y′]=[10a1][xy](x方向上的切变)
[ x ′ y ′ ] = [ 1 0 a 1 ] [ x y ] ( y 方 向 上 的 切 变 ) \begin{bmatrix} {x}'\\ {y}' \end{bmatrix} = \begin{bmatrix} 1 & 0\\ a & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\quad(y方向上的切变) [x′y′]=[1a01][xy](y方向上的切变)
【例】 y y y 方向上的切变( a = 1 a=1 a=1)

旋转(Rotate)
* 注意:默认情况下指的是绕原点旋转
根据旋转 θ \theta θ 角的矩阵 R θ \mathbf{R}_{\theta} Rθ,很容易推导出旋转 − θ -\theta −θ 角的矩阵 R − θ \mathbf{R}_{-\theta} R−θ,它等于 R θ \mathbf{R}_{\theta} Rθ 的转置:
R − θ = ( cos ( − θ ) − sin ( − θ ) sin ( − θ ) cos ( − θ ) ) = ( cos θ sin θ − sin θ cos θ ) = R θ T \mathbf{R}_{-\theta} =\begin{pmatrix} \cos (-\theta) & -\sin (-\theta) \\ \sin (-\theta) & \cos (-\theta) \end{pmatrix} = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} =\mathbf{R}_{\theta}^{T} R−θ=(cos(−θ)sin(−θ)−sin(−θ)cos(−θ))=(cosθ−sinθsinθcosθ)=RθT
又由定义,旋转 − θ -\theta −θ 角等于旋转 θ \theta θ 角的逆: R − θ = R θ − 1 \mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^{-1} R−θ=Rθ−1
因此我们得到这样一个结论:旋转矩阵的逆就等于旋转矩阵的转置,即 R θ − 1 = R θ T \mathbf{R}_{\theta}^{-1}=\mathbf{R}_{\theta}^{T} Rθ−1=RθT
齐次坐标(Homogenous Coordinates)
齐次坐标表示法
将原有的向量添加一维:
- 2D 点表示为: ( x , y , 1 ) T (x,y,1)^{T} (x,y,1)T
- 2D 向量表示为: ( x , y , 0 ) T (x,y,0)^{T} (x,y,0)T
在齐次坐标下,当 w ≠ 0 w\neq 0 w=0 时, ( x y w ) \begin{pmatrix} x\\ y\\ w \end{pmatrix} ⎝⎛xyw⎠⎞ 就表示 2D 点 ( x / w y / w 1 ) \begin{pmatrix} x/w\\ y/w\\ 1 \end{pmatrix} ⎝⎛x/wy/w1⎠⎞(即每一项都除以 w w w)。
平移(Translation)
此时,平移操作可以表示为:
( x ′ y ′ w ′ ) = ( 1 0 t x 0 1 t y 0 0 1 ) ⋅ ( x y 1 ) = ( x + t x y + t y 1 ) \begin{pmatrix} {x}'\\ {y}'\\ {w}' \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{pmatrix} x+t_x\\ y+t_y\\ 1 \end{pmatrix} ⎝⎛x′y′w′⎠⎞=⎝⎛100010txty1⎠⎞⋅⎝⎛xy1⎠⎞=⎝⎛x+txy+ty1⎠⎞
仿射变换(Affine Transformation)
仿射变换 = 线性变换 + 平移
用齐次坐标表示为:
( x ′ y ′ 1 ) = ( a b t x c d t y 0 0 1 ) ⋅ ( x y 1 ) \begin{pmatrix} {x}'\\ {y}'\\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} ⎝⎛x′y′1⎠⎞=⎝⎛ac0bd0txty1⎠⎞⋅⎝⎛xy1⎠⎞
上面的式子相当于 ( x ′ y ′ ) = ( a b c d ) ⋅ ( x y ) + ( t x t y ) \begin{pmatrix} x^{\prime} \\ y^{\prime} \end{pmatrix} =\begin{pmatrix} a & b \\ c & d \end{pmatrix}\cdot\begin{pmatrix} x \\ y \end{pmatrix}+\begin{pmatrix} t_{x} \\ t_{y} \end{pmatrix} (x′y′)=(acbd)⋅(xy)+(txty),所以顺序是先线性变换、再平移。
【例】
缩放(Scale): S ( s x , s y ) = ( s x 0 0 0 s y 0 0 0 1 ) \mathbf{S}\left ( s_x,s_y \right )= \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} S(sx,sy)=⎝⎛sx000sy0001⎠⎞
旋转(Rotation): R ( α ) = ( cos α − sin α 0 sin α cos α 0 0 0 1 ) \mathbf{R}\left ( \alpha \right )= \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} R(α)=⎝⎛cosαsinα0−sinαcosα0001⎠⎞
平移(Translation): T ( t x , t y ) = ( 1 0 t x 0 1 t y 0 0 1 ) \mathbf{T}\left ( t_x,t_y \right )= \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} T(tx,ty)=⎝⎛100010txty1⎠⎞
变换与顺序
- 各种变换之间的顺序是不能调换的,例如先旋转再平移 ≠ \neq = 先平移再旋转。因为矩阵乘法没有交换律。
- 但是矩阵乘法有结合律,所以多次变换的矩阵可以合成为一个矩阵,这一个矩阵就代表了所有的变换。
- 例如 A n ⋯ A 2 ⋅ A 1 \mathbf{A}_n \cdots \mathbf{A}_2\cdot \mathbf{A}_1 An⋯A2⋅A1 最终可以写成一个 A \mathbf{A} A,代表所有的变换。
A n ( ⋯ A 2 ( A 1 ( x ) ) ) = A n ⋯ A 2 ⋅ A 1 ⋅ ( x y 1 ) = A ⋅ ( x y 1 ) A_n\left ( \cdots A_2\left ( A_1\left ( \mathbf{x} \right ) \right ) \right ) \\ =\mathbf{A}_n \cdots \mathbf{A}_2\cdot \mathbf{A}_1 \cdot \begin{pmatrix} x\\ y\\ 1 \\ \end{pmatrix}\\ = \mathbf{A}\cdot \begin{pmatrix} x\\ y\\ 1 \\ \end{pmatrix} An(⋯A2(A1(x)))=An⋯A2⋅A1⋅⎝⎛xy1⎠⎞=A⋅⎝⎛xy1⎠⎞
- 例如 A n ⋯ A 2 ⋅ A 1 \mathbf{A}_n \cdots \mathbf{A}_2\cdot \mathbf{A}_1 An⋯A2⋅A1 最终可以写成一个 A \mathbf{A} A,代表所有的变换。
- 对某一向量顺次应用的一系列操作,都要从右往左地写在向量左边(左乘)。
- 例如上面的式子,依次使用 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An,矩阵相乘时为 A n ⋯ A 2 ⋅ A 1 \mathbf{A}_n \cdots \mathbf{A}_2\cdot \mathbf{A}_1 An⋯A2⋅A1。
- 一个矩阵当然也可以分解成若干个矩阵顺次相乘。分解可能有很多种结果,所有分解最终效果相同。
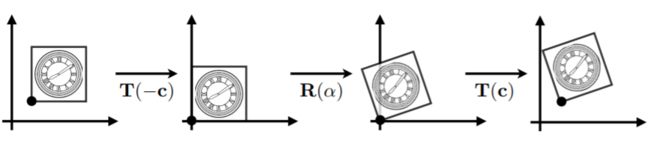
【例】绕某一点 c \mathbf{c} c(非原点)旋转 α \alpha α 角的操作,可以分解为如下三步:
- 将点 c \mathbf{c} c 平移至原点
- 旋转 α \alpha α 角
- 平移回 c \mathbf{c} c 点
写成矩阵乘法的形式: T ( c ) ⋅ R ( α ) ⋅ T ( − c ) \mathbf{T}(\mathbf{c})\cdot \mathbf{R}(\alpha )\cdot \mathbf{T}(-\mathbf{c}) T(c)⋅R(α)⋅T(−c) (注意是从右往左乘)
【例】一个切变可以被分解成旋转-缩放-旋转三步。
- 推导过程:
[ 1 1 0 1 ] = R 2 [ σ 1 0 0 σ 2 ] R 1 = [ 0.8507 − 0.5257 0.5257 0.8507 ] [ 1.618 0 0 0.618 ] [ 0.5257 0.8507 − 0.8507 0.5257 ] = rotate ( 31. 7 ∘ ) scale ( 1.618 , 0.618 ) rotate ( − 58. 3 ∘ ) \begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix} \\=\mathbf{R}_{2}\begin{bmatrix} \sigma_{1} & 0 \\ 0 & \sigma_{2} \end{bmatrix} \mathbf{R}_{1} \\ =\begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix}\begin{bmatrix} 1.618 & 0 \\ 0 & 0.618 \end{bmatrix}\begin{bmatrix} 0.5257 & 0.8507 \\ -0.8507 & 0.5257 \end{bmatrix} \\ =\text{rotate}\left(31.7^{\circ}\right) \text { scale}(1.618,0.618) \text { rotate}\left(-58.3^{\circ}\right) [1011]=R2[σ100σ2]R1=[0.85070.5257−0.52570.8507][1.618000.618][0.5257−0.85070.85070.5257]=rotate(31.7∘) scale(1.618,0.618) rotate(−58.3∘)
- 图形演示:
3D 变换
3D 点、向量的齐次坐标表示
3D 空间中的点和向量可以表示为:
- 3D 点表示为: ( x , y , z , 1 ) T (x,y,z,1)^{T} (x,y,z,1)T
- 3D 向量表示为: ( x , y , z , 0 ) T (x,y,z,0)^{T} (x,y,z,0)T
当 w ≠ 0 w\neq 0 w=0 时, ( x y z w ) \begin{pmatrix} x\\ y\\ z\\ w \end{pmatrix} ⎝⎜⎜⎛xyzw⎠⎟⎟⎞ 就表示 3D 点 ( x / w y / w z / w 1 ) \begin{pmatrix} x/w\\ y/w\\ z/w\\ 1 \end{pmatrix} ⎝⎜⎜⎛x/wy/wz/w1⎠⎟⎟⎞ 。
三维空间中的旋转
绕谁转,谁不变。用代数余子式的方法去理解下面的式子:
绕 x x x 轴旋转: R x ( α ) = ( 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ) \mathbf{R}_{x}(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} Rx(α)=⎝⎜⎜⎛10000cosαsinα00−sinαcosα00001⎠⎟⎟⎞
绕 y y y 轴旋转: R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) \mathbf{R}_{y}(\alpha) = \begin{pmatrix} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} Ry(α)=⎝⎜⎜⎛cosα0−sinα00100sinα0cosα00001⎠⎟⎟⎞ (注意负号的位置)
绕 z z z 轴旋转: R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) \mathbf{R}_{z}(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} Rz(α)=⎝⎜⎜⎛cosαsinα00−sinαcosα0000100001⎠⎟⎟⎞
罗德里格斯旋转公式(Rodrigues’ Rotation Formula)
绕过原点的 n \mathbf{n} n 轴,旋转 α \alpha α 角度:(其中 I \mathbf{I} I 是单位阵)
R ( n , α ) = cos ( α ) I + ( 1 − cos ( α ) ) n n T + sin ( α ) ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n n}^{T}+\sin (\alpha) \underbrace{\begin{pmatrix} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{pmatrix}}_{\mathbf{N}} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)N ⎝⎛0nz−ny−nz0nxny−nx0⎠⎞
Viewing transformation
MVP:
- 模型变换(model transformation)—— Find a good place and arrange people
- 视图变换(view transformation)—— Find a good “angle” to put the camera
- 投影变换(projection transformation)—— Cheese!
视图变换(View / Camera transformation)
定义相机:
- 相机的位置 e ⃗ \vec{e} e
- 观察方向 g ^ \hat{g} g^
- 向上方向 t ^ \hat{t} t^ (假定垂直于观察方向)
容易得到相机的右方向是 g ^ × t ^ \hat{g} \times \hat{t} g^×t^
把相机固定到原点,并且向上方向为 y y y 轴方向,看向 − z -z −z 轴的方向(观察方向)。让物体跟着相机走。
使用矩阵 M v i e w M_{view} Mview 来完成这一变换:
- M v i e w = R v i e w T v i e w M_{view}=R_{view}T_{view} Mview=RviewTview
- 把 e ⃗ \vec{e} e 平移到原点: T v i e w = [ 1 0 0 − x e 0 1 0 − y e 0 0 1 − z e 0 0 0 1 ] T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{bmatrix} Tview=⎣⎢⎢⎡100001000010−xe−ye−ze1⎦⎥⎥⎤
- 旋转: g ^ → − Z \hat{g} \rightarrow -Z g^→−Z 轴, t ^ → Y \hat{t} \rightarrow Y t^→Y 轴, ( g ^ × t ^ ) → X \left ( \hat{g} \times \hat{t} \right )\rightarrow X (g^×t^)→X 轴
- 考虑其逆过程: Z Z Z 轴 → − g ^ \rightarrow -\hat{g} →−g^, Y Y Y 轴 → t ^ \rightarrow \hat{t} →t^, X X X 轴 → ( g ^ × t ^ ) \rightarrow \left ( \hat{g} \times \hat{t} \right ) →(g^×t^)
- 由于旋转矩阵的逆等于旋转矩阵的转置,可以得到:
R v i e w − 1 = [ x g ^ × t ^ x t x − g 0 y g ^ × t ^ y t y − g 0 z g ^ × t ^ z t z − g 0 0 0 0 1 ] ⇒ R v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] R_{view}^{-1}=\begin{bmatrix} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0 \\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0 \\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \quad \Rightarrow \quad R_{view}=\begin{bmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rview−1=⎣⎢⎢⎡xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001⎦⎥⎥⎤⇒Rview=⎣⎢⎢⎡xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001⎦⎥⎥⎤
投影变换(Projection transformation)
正交投影(Orthographic projection)
简单的理解正交投影(直观理解):
- 相机在原点, looking at − Z -Z −Z, up at Y Y Y
- 直接丢弃 Z Z Z 坐标
- 将生成的矩形平移并缩放到 [ − 1 , 1 ] 2 \left [ -1,1 \right ]^{2} [−1,1]2
实际上的做法:
把一个长方体 [ l , r ] × [ b , t ] × [ f , n ] \left [ l,r \right ]\times \left [ b,t \right ]\times \left [ f,n \right ] [l,r]×[b,t]×[f,n] map(映射) 到 标准视体 [ − 1 , 1 ] 3 \left [ -1,1 \right ]^{3} [−1,1]3
- 将长方体中心平移到原点 Translate (center to origin) first
- 缩放至标准大小 then scale (length/width/height to 2 2 2)
M o r t h o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 l + r l − r 0 2 t − b 0 b + t b − t 0 0 2 n − f f + n f − n 0 0 0 1 ] M_{ortho}=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & \frac{l + r}{l -r}\\ 0 & \frac{2}{t-b} & 0 & \frac{b + t}{b -t}\\ 0 & 0 & \frac{2}{n-f} & \frac{f + n}{f-n}\\ 0 & 0 & 0 & 1 \end{bmatrix} Mortho=⎣⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎤=⎣⎢⎢⎡r−l20000t−b20000n−f20l−rl+rb−tb+tf−nf+n1⎦⎥⎥⎤
注意: n > f n > f n>f (Looking at / along -Z is making near and far not intuitive(不符合直觉))

透视投影(Perspective projection)
- 更常用,更符合人眼的直觉 Most common in Computer Graphics, art, visual system
- 近大远小,远处的物体看起来小 Further objects are smaller
- 平行线不再平行。平行线在远处看起来似乎会“相交”于一点 Parallel lines not parallel; converge to single point
如何做透视投影: M p e r s p = M o r t h o M p e r s p → o r t h o M_{persp}=M_{ortho} M_{persp \rightarrow ortho} Mpersp=MorthoMpersp→ortho
- 先把视锥体挤压成长方体 M p e r s p → o r t h o M_{persp \rightarrow ortho} Mpersp→ortho First “squish” the frustum into a cuboid (n -> n, f -> f)
- 做正交投影 M o r t h o M_{ortho} Mortho Do orthographic projection
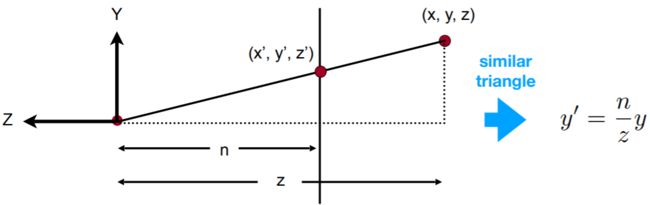
求解 M p e r s p → o r t h o M_{persp \rightarrow ortho} Mpersp→ortho 的中心思想: 寻找变换后 点 ( x ’ , y ’ , z ’ ) (x’, y’, z’) (x’,y’,z’) 和变换前 点 ( x , y , z ) (x, y, z) (x,y,z) 的关系
在挤压的过程中,
- 近平面上点坐标不会变 Any point on the near plane will not change
- 远平面上点 z z z 坐标不会变 Any point’s z on the far plane will not change
- 远平面中心点不会变(挤压之后它还是中心)
求解出来得: M p e r s p → o r t h o = ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) M_{persp \rightarrow ortho}=\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix} Mpersp→ortho=⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞
综上: M p e r s p = M o r t h o M p e r s p → o r t h o = M o r t h o ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) = ( 2 n r − l 0 l + r l − r 0 0 2 n t − b b + t b − t 0 0 0 n + f n − f 2 f n f − n 0 0 1 0 ) \displaystyle M_{persp} \\ =M_{ortho} M_{persp \rightarrow ortho} \\ =M_{ortho} \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix} \\ = \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0 \end{pmatrix} Mpersp=MorthoMpersp→ortho=Mortho⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞=⎝⎜⎜⎛r−l2n0000t−b2n00l−rl+rb−tb+tn−fn+f100f−n2fn0⎠⎟⎟⎞
参考:
Steve Marschner and Peter Shirley. Fundamentals of Computer Graphics. 第四版.
GAMES101. https://www.bilibili.com/video/BV1X7411F744?p=3.
变换(二维与三维)课件. https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_03.pdf.
变换(模型、视图、投影)课件. https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_04.pdf.