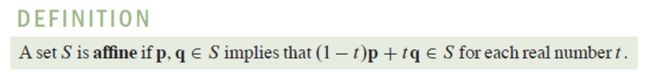Chapter 8 (The Geometry of Vector Spaces): Affine combinations (仿射组合)
- This chapter begins with geometric ideas that are already familiar to you. Affine combinations of vectors generalize the concepts of lines and planes to higher dimensions and describe the mathematical objects formed when subspaces are shifted away from the origin. Hyperplanes are a generalization of planes, and polytopes are a generalization of polygons.
- The geometric objects studied in this chapter include line segments, solid triangles and polygons, specials types of curves and surfaces, and generalizations to sets in more than three dimensions. These objects form the building blocks for applications to computer graphics and to linear programming.
Contents
- Affine combinations
- Affine hull / Affine span (仿射包 / 仿射生成集)
-
- Definition
- Decide whether a point is in an affine hull
- Affine set
- Connection with subspaces of R n \R^n Rn
-
- Flats (平面)
- Affine set ⇔ \Leftrightarrow ⇔ Flat
- A geometric view of affine combinations
- Connection with computer graphics
- References
Affine combinations
- Given vectors (or “points”) v 1 , v 2 , . . . , v p \boldsymbol v_1, \boldsymbol v_2,...,\boldsymbol v_p v1,v2,...,vp in R n \R^n Rn and scalars c 1 , . . . , c p c_1,...,c_p c1,...,cp, an affine combination of v 1 , v 2 , . . . , v p \boldsymbol v_1, \boldsymbol v_2,...,\boldsymbol v_p v1,v2,...,vp is a linear combination
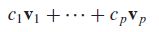 such that the weights satisfy c 1 + . . . + c p = 1 c_1+...+ c_p= 1 c1+...+cp=1.
such that the weights satisfy c 1 + . . . + c p = 1 c_1+...+ c_p= 1 c1+...+cp=1.
Affine hull / Affine span (仿射包 / 仿射生成集)
Definition
- The affine hull of a single point v 1 \boldsymbol v_1 v1 is just the set { v 1 } \{\boldsymbol v_1\} {v1}. The affine hull of two distinct points is often written in a special way. Suppose y = c 1 v 1 + c 2 v 2 \boldsymbol y = c_1\boldsymbol v_1+ c_2\boldsymbol v_2 y=c1v1+c2v2 with c 1 + c 2 = 1 c_1 + c_2 = 1 c1+c2=1. Write t t t in place of c 2 c_2 c2, so that c 1 = 1 − t c_1= 1- t c1=1−t . Then the affine hull of { v 1 , v 2 } \{\boldsymbol v_1, \boldsymbol v_2\} {v1,v2} is the set
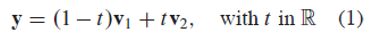 This set of points includes v 1 \boldsymbol v_1 v1 (when t = 0 t= 0 t=0) and v 2 \boldsymbol v_2 v2 (when t = 1 t= 1 t=1). If v 2 = v 1 \boldsymbol v_2=\boldsymbol v_1 v2=v1, then (1) again describes just one point. Otherwise, (1) describes the line through v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2. To see this, rewrite (1) in the form
This set of points includes v 1 \boldsymbol v_1 v1 (when t = 0 t= 0 t=0) and v 2 \boldsymbol v_2 v2 (when t = 1 t= 1 t=1). If v 2 = v 1 \boldsymbol v_2=\boldsymbol v_1 v2=v1, then (1) again describes just one point. Otherwise, (1) describes the line through v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2. To see this, rewrite (1) in the form
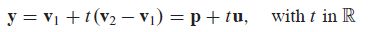 where p \boldsymbol p p is v 1 \boldsymbol v_1 v1 and u \boldsymbol u u is v 2 − v 1 \boldsymbol v_2-\boldsymbol v_1 v2−v1.
where p \boldsymbol p p is v 1 \boldsymbol v_1 v1 and u \boldsymbol u u is v 2 − v 1 \boldsymbol v_2-\boldsymbol v_1 v2−v1.
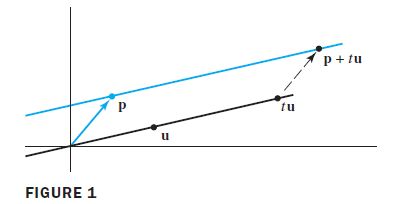
Figure 2 uses the original points v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2, and displays aff { v 1 , v 2 } \text {aff }\{\boldsymbol v_1,\boldsymbol v_2\} aff {v1,v2} as the line through v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2.

- The next example takes a fresh look at a familiar set—the set of all solutions of a system A x = b A\boldsymbol x =\boldsymbol b Ax=b.
EXAMPLE 3
- Suppose that the solutions of an equation A x = b A\boldsymbol x =\boldsymbol b Ax=b are all of the form x = x 3 u + p \boldsymbol x= x_3\boldsymbol u+\boldsymbol p x=x3u+p, (通解 + 特解 的形式)
 Find points v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2 such that the solution set of A x = b A\boldsymbol x=\boldsymbol b Ax=b is aff { v 1 , v 2 } \text{aff }\{\boldsymbol v_1, \boldsymbol v_2\} aff {v1,v2}.
Find points v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2 such that the solution set of A x = b A\boldsymbol x=\boldsymbol b Ax=b is aff { v 1 , v 2 } \text{aff }\{\boldsymbol v_1, \boldsymbol v_2\} aff {v1,v2}.
SOLUTION
- The solution set is a line through p \boldsymbol p p in the direction of u \boldsymbol u u. Since aff { v 1 , v 2 } \text{aff }\{\boldsymbol v_1,\boldsymbol v_2\} aff {v1,v2} is a line through v 1 \boldsymbol v_1 v1 and v 2 \boldsymbol v_2 v2, identify two points on the line x = x 3 u + p \boldsymbol x= x_3\boldsymbol u+\boldsymbol p x=x3u+p. Two simple choices appear when x 3 = 0 x_3= 0 x3=0 and x 3 = 1 x_3= 1 x3=1. That is, take v 1 = p \boldsymbol v_1=\boldsymbol p v1=p and v 2 = u + p \boldsymbol v_2=\boldsymbol u+\boldsymbol p v2=u+p, so that

- In this case, the solution set is described as the set of all affine combinations of the form

Decide whether a point is in an affine hull
In the statement of Theorem 1, the point v 1 \boldsymbol v_1 v1 could be replaced by any of the other points in the list v 1 , . . . , v p \boldsymbol v_1,..., \boldsymbol v_p v1,...,vp: Only the notation in the proof would change.
PROOF
- [Hint: y = ( 1 − c 2 − . . . − c p ) v 1 + c 2 v 2 + . . . + c p v p \boldsymbol y=(1-c_2-...-c_p)\boldsymbol v_1+c_2\boldsymbol v_2+...+c_p\boldsymbol v_p y=(1−c2−...−cp)v1+c2v2+...+cpvp]
- We can judge whether an arbitrary vector y \boldsymbol y y is an affine combination of { v 1 , . . . , v n } \{\boldsymbol v_1,...,\boldsymbol v_n\} {v1,...,vn} by using Theorem 1. But the question can be answered more directly if the chosen points v i \boldsymbol v_i vi are a basis for R n \R^n Rn. For example, let B = { b 1 , . . . , b n } \mathcal B = \{\boldsymbol b_1,...,\boldsymbol b_n\} B={b1,...,bn} be such a basis. Then any y \boldsymbol y y in R n \R^n Rn is a unique linear combination of b 1 , . . . , b n \boldsymbol b_1,...,\boldsymbol b_n b1,...,bn. This combination is an affine combination of the b \boldsymbol b b’s if and only if the weights sum to 1.
Affine set
集合 S S S 是仿射的
- Geometrically, a set is affine if whenever two points are in the set, the entire line through these points is in the set. (If S S S contains only one point, p \boldsymbol p p, then the line through p \boldsymbol p p and p \boldsymbol p p is just a point, a “degenerate” line.)
- Algebraically, for a set S S S to be affine, the definition requires that every affine combination of two points of S S S belong to S S S. Remarkably, this is equivalent to requiring that S S S contain every affine combination of an arbitrary number of points of S S S.
- Suppose that S S S is affine and use induction (数学归纳法) on the number m m m of points of S S S occurring in an affine combination.
- (i). When m m m is 1 or 2, an affine combination of m m m points of S S S lies in S S S, by the definition of an affine set.
- (ii). Now, assume that every affine combination of k k k or fewer points of S S S yields a point in S S S, and consider a combination of k + 1 k+ 1 k+1 points. Take v i \boldsymbol v_i vi in S S S for i = 1 , . . . , k + 1 i=1,..., k+ 1 i=1,...,k+1, and let y = c 1 v 1 + . . . + c k v k + c k + 1 v k + 1 \boldsymbol y = c_1\boldsymbol v_1+...+c_k\boldsymbol v_k+ c_{k+1}\boldsymbol v_{k+1} y=c1v1+...+ckvk+ck+1vk+1, where c 1 + . . . + c k + 1 = 1 c_1+...+ c_{k+1}= 1 c1+...+ck+1=1. Since the c i c_i ci ’s sum to 1, at least one of them must not be equal to 1. By reindexing the v i \boldsymbol v_i vi and c i c_i ci , if necessary, we may assume that c k + 1 ≠ 1 c_{k+1}\neq 1 ck+1=1. Let t = c 1 + . . . + c k t= c_1+...+ c_k t=c1+...+ck. Then t = 1 − c k + 1 ≠ 0 t= 1- c_{k+1} \neq 0 t=1−ck+1=0, and

By the induction hypothesis, the point z = ( c 1 / t ) v 1 + . . . + ( c k / t ) v k \boldsymbol z=(c_1/t)\boldsymbol v_1+...+(c_k/t)\boldsymbol v_k z=(c1/t)v1+...+(ck/t)vk is in S S S. Thus (6) displays y \boldsymbol y y as an affine combination of two points in S S S. By the principle of induction, every affine combination of such points lies in S S S. That is, aff S ⊂ S \text{aff } S\subset S aff S⊂S. The reverse inclusion, S ⊂ aff S S\subset \text{aff }S S⊂aff S, always applies.
Connection with subspaces of R n \R^n Rn
Flats (平面)
translate: 平移
- For example, in R 3 \R^3 R3, the proper subspaces consist of the origin 0 \boldsymbol 0 0, the set of all lines through 0 \boldsymbol 0 0, and the set of all planes through 0 \boldsymbol 0 0. Thus the proper flats in R 3 \R^3 R3 are points (zero-dimensional), lines (one-dimensional), and planes (two-dimensional), which may or may not pass through the origin.
- The next theorem shows that these geometric descriptions of lines and planes in R 3 \R^3 R3 (as translates of subspaces) actually coincide with their earlier algebraic descriptions as sets of all affine combinations of two or three points, respectively.
Affine set ⇔ \Leftrightarrow ⇔ Flat
PROOF
- Suppose that S S S is affine. Let p \boldsymbol p p be any fixed point in S S S and let W = S + ( − p ) W= S+(-\boldsymbol p) W=S+(−p), so that S = W + p S= W +\boldsymbol p S=W+p. To show that S S S is a flat, it suffices to show that W W W is a subspace of R n \R^n Rn.
- Since p \boldsymbol p p is in S S S, the zero vector is in W W W. To show that W W W is closed under sums and scalar multiples, it suffices to show that if u 1 \boldsymbol u_1 u1 and u 2 \boldsymbol u_2 u2 are elements of W W W, then u 1 + t u 2 \boldsymbol u_1+ t\boldsymbol u_2 u1+tu2 is in W W W for every real t t t. Since u 1 \boldsymbol u_1 u1 and u 2 \boldsymbol u_2 u2 are in W W W , there exist s 1 \boldsymbol s_1 s1 and s 2 \boldsymbol s_2 s2 in S S S such that
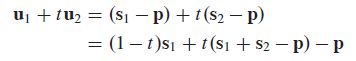 Let y = s 1 + s 2 − p \boldsymbol y= s_1 + s_2 -\boldsymbol p y=s1+s2−p. Then y \boldsymbol y y is an affine combination of points in S S S. Since S S S is affine, y \boldsymbol y y is in S S S. But then ( 1 − t ) s 1 + t y (1- t)\boldsymbol s_1+ t\boldsymbol y (1−t)s1+ty is also in S S S. So u 1 + t u 2 \boldsymbol u_1 + t\boldsymbol u_2 u1+tu2 is in − p + S = W -\boldsymbol p+ S= W −p+S=W. This shows that W W W is a subspace of R n \R^n Rn. Thus S S S is a flat, because S = W + p S= W +\boldsymbol p S=W+p.
Let y = s 1 + s 2 − p \boldsymbol y= s_1 + s_2 -\boldsymbol p y=s1+s2−p. Then y \boldsymbol y y is an affine combination of points in S S S. Since S S S is affine, y \boldsymbol y y is in S S S. But then ( 1 − t ) s 1 + t y (1- t)\boldsymbol s_1+ t\boldsymbol y (1−t)s1+ty is also in S S S. So u 1 + t u 2 \boldsymbol u_1 + t\boldsymbol u_2 u1+tu2 is in − p + S = W -\boldsymbol p+ S= W −p+S=W. This shows that W W W is a subspace of R n \R^n Rn. Thus S S S is a flat, because S = W + p S= W +\boldsymbol p S=W+p.
- Since p \boldsymbol p p is in S S S, the zero vector is in W W W. To show that W W W is closed under sums and scalar multiples, it suffices to show that if u 1 \boldsymbol u_1 u1 and u 2 \boldsymbol u_2 u2 are elements of W W W, then u 1 + t u 2 \boldsymbol u_1+ t\boldsymbol u_2 u1+tu2 is in W W W for every real t t t. Since u 1 \boldsymbol u_1 u1 and u 2 \boldsymbol u_2 u2 are in W W W , there exist s 1 \boldsymbol s_1 s1 and s 2 \boldsymbol s_2 s2 in S S S such that
- Conversely, suppose S S S is a flat. That is, S = W + p S= W +\boldsymbol p S=W+p for some p ∈ R n \boldsymbol p\in \R^n p∈Rn and some subspace W W W . To show that S S S is affine, it suffices to show that for any pair s 1 \boldsymbol s_1 s1 and s 2 \boldsymbol s_2 s2 of points in S S S, the line through s 1 \boldsymbol s_1 s1 and s 2 \boldsymbol s_2 s2 lies in S S S. By definition of W W W, there exist u 1 \boldsymbol u_1 u1 and u 2 \boldsymbol u_2 u2 in W W W such that s 1 = u 1 + p \boldsymbol s_1= \boldsymbol u_1+\boldsymbol p s1=u1+p and s 2 = u 2 + p \boldsymbol s_2=\boldsymbol u_2+\boldsymbol p s2=u2+p. So, for each real t t t,
 Since W W W is a subspace, ( 1 − t ) u 1 + t u 2 ∈ W (1- t)\boldsymbol u_1+ t\boldsymbol u_2\in W (1−t)u1+tu2∈W and so ( 1 − t ) s 1 + t s 2 ∈ W + p = S (1- t)s_1+ t s_2 \in W +\boldsymbol p= S (1−t)s1+ts2∈W+p=S. Thus S S S is affine.
Since W W W is a subspace, ( 1 − t ) u 1 + t u 2 ∈ W (1- t)\boldsymbol u_1+ t\boldsymbol u_2\in W (1−t)u1+tu2∈W and so ( 1 − t ) s 1 + t s 2 ∈ W + p = S (1- t)s_1+ t s_2 \in W +\boldsymbol p= S (1−t)s1+ts2∈W+p=S. Thus S S S is affine.
Remark: Notice the key role that definitions play in this proof. For example, the first part assumes that S S S is affine and seeks to show that S S S is a flat. By definition, a flat is a translate of a subspace. By choosing p \boldsymbol p p in S S S and defining W = S + ( − p ) W= S +(-\boldsymbol p) W=S+(−p), the set S S S is translated to the origin and S = W + p S= W +\boldsymbol p S=W+p. It remains to show that W W W is a subspace, for then S S S will be a translate of a subspace and hence a flat.
A geometric view of affine combinations
- Theorem 3 provides a geometric way to view the affine hull of a set: it is the flat that consists of all the affine combinations of points in the set.
- For instance, the affine combination of two linearly independent vectors (points) is just the line through these two points; the affine combination of three linearly independent vectors (points) is the plane through these three points. (In Figure 3, b 1 , b 2 \boldsymbol b_1, \boldsymbol b_2 b1,b2, and b 3 \boldsymbol b_3 b3 is a basis of R 3 \R^3 R3.

- For instance, the affine combination of two linearly independent vectors (points) is just the line through these two points; the affine combination of three linearly independent vectors (points) is the plane through these three points. (In Figure 3, b 1 , b 2 \boldsymbol b_1, \boldsymbol b_2 b1,b2, and b 3 \boldsymbol b_3 b3 is a basis of R 3 \R^3 R3.
EXERCISE 13
- Suppose { v 1 , v 2 , v 3 } \{\boldsymbol v_1, \boldsymbol v_2,\boldsymbol v_3\} {v1,v2,v3} is a basis for R 3 \R^3 R3. Show that S p a n { v 2 − v 1 , v 3 − v 1 } Span\{\boldsymbol v_2-\boldsymbol v_1 ,\boldsymbol v_3-\boldsymbol v_1\} Span{v2−v1,v3−v1} is a plane in R 3 \R^3 R3.
SOLUTION
- [Hint: S p a n { v 2 − v 1 , v 3 − v 1 } Span\{\boldsymbol v_2-\boldsymbol v_1 ,\boldsymbol v_3-\boldsymbol v_1\} Span{v2−v1,v3−v1} is a plane if and only if { v 2 − v 1 , v 3 − v 1 } \{\boldsymbol v_2-\boldsymbol v_1 ,\boldsymbol v_3-\boldsymbol v_1\} {v2−v1,v3−v1} is linearly independent.]
EXERCISE 14
- Show that if { v 1 , v 2 , v 3 } \{\boldsymbol v_1, \boldsymbol v_2,\boldsymbol v_3\} {v1,v2,v3} is a basis for R 3 \R^3 R3, then aff { v 1 , v 2 , v 3 } \text{aff }\{\boldsymbol v_1, \boldsymbol v_2,\boldsymbol v_3\} aff {v1,v2,v3} is the plane through v 1 , v 2 , \boldsymbol v_1, \boldsymbol v_2, v1,v2, and v 3 \boldsymbol v_3 v3.
SOLUTION
- It suffices to show that aff { v 1 , v 2 , v 3 } \text{aff }\{\boldsymbol v_1, \boldsymbol v_2,\boldsymbol v_3\} aff {v1,v2,v3} is the translation of a subspace. if y ∈ aff { v 1 , v 2 , v 3 } \boldsymbol y\in \text{aff }\{\boldsymbol v_1, \boldsymbol v_2,\boldsymbol v_3\} y∈aff {v1,v2,v3}, then y − v 1 ∈ S p a n { v 2 − v 1 , v 3 − v 1 } \boldsymbol y-\boldsymbol v_1\in Span\{\boldsymbol v_2-\boldsymbol v_1,\boldsymbol v_3-\boldsymbol v_1\} y−v1∈Span{v2−v1,v3−v1}. Thus y ∈ v 1 + S p a n { v 2 − v 1 , v 3 − v 1 } \boldsymbol y\in \boldsymbol v_1+Span\{\boldsymbol v_2-\boldsymbol v_1,\boldsymbol v_3-\boldsymbol v_1\} y∈v1+Span{v2−v1,v3−v1}.
EXERCISE 16
- Let v ∈ R n \boldsymbol v\in \R^n v∈Rn and let k ∈ R k\in \R k∈R. Prove that S = { x ∈ R n : x ⋅ v = k } S =\{\boldsymbol x\in \R^n:\boldsymbol x\cdot\boldsymbol v=k\} S={x∈Rn:x⋅v=k} is an affine subset of R n \R^n Rn.
SOLUTION
- W = { x ∈ R n : x ⋅ v = 0 } W =\{\boldsymbol x\in \R^n:\boldsymbol x\cdot\boldsymbol v=0\} W={x∈Rn:x⋅v=0} is a subspace of R n \R^n Rn. Suppose p ⋅ v = k \boldsymbol p\cdot\boldsymbol v=k p⋅v=k, then S = W + p S=W+\boldsymbol p S=W+p.
Connection with computer graphics
- The next theorem provides another view of affine combinations, which for R 2 \R^2 R2 and R 3 \R^3 R3 is closely connected to applications in computer graphics. (See the next section and Section 2.7)
EXAMPLE 4
- Let
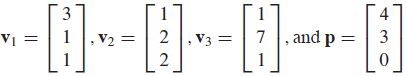 Write p \boldsymbol p p as an affine combination of v 1 , v 2 \boldsymbol v_1, \boldsymbol v_2 v1,v2, and v 3 \boldsymbol v_3 v3, if possible.
Write p \boldsymbol p p as an affine combination of v 1 , v 2 \boldsymbol v_1, \boldsymbol v_2 v1,v2, and v 3 \boldsymbol v_3 v3, if possible.
SOLUTION
- Row reduce the augmented matrix for the equation
 To simplify the arithmetic, move the fourth row of 1’s to the top (equivalent to three row interchanges). After this, the number of arithmetic operations here is basically the same as the number needed for the method using Theorem 1.
To simplify the arithmetic, move the fourth row of 1’s to the top (equivalent to three row interchanges). After this, the number of arithmetic operations here is basically the same as the number needed for the method using Theorem 1.
 Thus
Thus
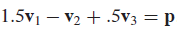

References
- L i n e a r Linear Linear a l g e b r a algebra algebra a n d and and i t s its its a p p l i c a t i o n s applications applications