3D-2D三维重建：PnP

简介

PnP（Perspective-n-Point）描述了当我们已知n个世界坐标系下的3D空间点以及它们的2D归一化相机坐标系下的坐标时，如何估计相机位姿的方法。通常最少需要4对3D-2D点对（其中之一用于验证结果），就可以解出PnP问题。尤其是在双目或RGB-D的视觉里程计中，点的空间坐标可以由$s{K}^{-1}x$直接求出，$s$为像素点的深度值，即可直接使用PnP估计相机运动。

PnP问题解法有很多，线性方法有直接线性变换法、P3P、EPnP、UPnP等，还可以采用非线性优化的方法、构建最小二乘问题迭代求解，最常用的是BA调整（Bundle Adjustment）。OpenCV中对上述多数方法都进行了集成，详情可见：solvePnP()。

PnP只是求解相机位姿的方法，求解出来的位姿均是相机相对世界坐标系的变换关系$T_{wc}$。对于那些没有3D匹配点的2D-2D匹配点对，估计其对应的3D点仍需采用三角化方式。

原理

直接线性变换法

直接线性变换法依据相机投影的基本原理，通过线性变换求解目标值。即$$sx=PX$$其中，$x=(u,v,1{)}^T$为像素点的归一化坐标；$P=[R|T]$为$3\times 4$的相机投影矩阵。
在求解PnP问题时，旋转矩阵$R$和平移矩阵$T$是待求的变量，由于$P$一共有12维，而每对点对能提供2个约束，因此最少需要6对点对，才能实现PnP问题的线性求解。

需要注意的一点是，上述公式默认相机内参数矩阵$K$已知，所以$x$采用的是归一化平面坐标，在求解PnP问题时去掉了$K$的影响，对应的solvePnP()中的3D点为相机坐标系下的齐次坐标；如果$K$未知，也可以使用PnP估计$K$,$R$,$T$，只不过上述推导过程多了内参$K$、求解时未知量增多，效果差一些而已，对应的solvePnP()中的3D点为世界坐标系下的坐标。

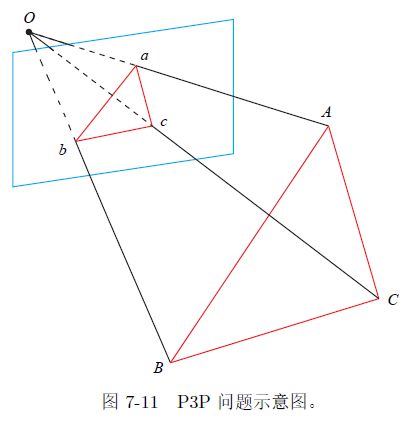
P3P

P3P也是一种求解PnP问题的方法，不过只使用3对点对即可，基本原理是根据世界坐标系下的3D点和像素坐标系下2D点，得到对应的相机坐标系的3D点，将问题转化成3D-3D问题，通过迭代最近点（Iterative Closest Point, ICP）方法进行求解。P3P方法只是根据上述3D-2D点对得到相机坐标系下的3D坐标，而进一步估计相机位姿$R$和$T$的过程仍需借助ICP方法完成。

BA优化

上述线性方法总是先求相机位姿$P$，再求空间点坐标，而非线性优化则将相机位姿和空间点坐标作为变量，同时进行优化。

上述方法的原理推导过程，请参考《视觉SLAM14讲-chapter7.7：3D-2D:PnP》，这里不再赘述。

备注：ICP问题

迭代最近点（Iterative Closest Point, ICP）方法用于解决已知3D-3D点对情况下，求解点的空间坐标的问题。在这个过程中，只涉及由世界坐标系到相机坐标系的转换，而与相机模型无关。3D点对满足的关系如下：$$P_2=R{P}_1+T$$其中，$P_1$是相机坐标系下的坐标；$P_2$是世界坐标系下的坐标。
可以通过SVD分解或非线性优化的方式求解ICP问题。

代码

以下代码使用OpenCV提供的EPNP方法求接PnP问题，同时使用RGBD相机的深度图计算3D点位置。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

void find_feature_matches (
    const Mat& img_1, const Mat& img_2,
    std::vector<KeyPoint>& keypoints_1,
    std::vector<KeyPoint>& keypoints_2,
    std::vector< DMatch >& matches );

// 像素坐标转相机归一化坐标
Point2d pixel2cam ( const Point2d& p, const Mat& K );

int main ( int argc, char** argv )
{
    //-- 读取图像
    Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
    Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );

    vector<KeyPoint> keypoints_1, keypoints_2;
    vector<DMatch> matches;
    find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
    cout<<"一共找到了"<<matches.size() <<"组匹配点"<<endl;

    // 建立3D点
    Mat d1 = imread ( argv[3], CV_LOAD_IMAGE_UNCHANGED );       // 深度图为16位无符号数，单通道图像
    Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector<Point3f> pts_3d;
    vector<Point2f> pts_2d;
    for ( DMatch m:matches )
    {
        ushort d = d1.ptr<unsigned short> (int ( keypoints_1[m.queryIdx].pt.y )) [ int ( keypoints_1[m.queryIdx].pt.x ) ];
        if ( d == 0 )   // bad depth
            continue;
        float dd = d/5000.0;
        Point2d p1 = pixel2cam ( keypoints_1[m.queryIdx].pt, K );// p1为归一化坐标：x
        pts_3d.push_back ( Point3f ( p1.x*dd, p1.y*dd, dd ) );	 // p1*dd代表sx, 也等于PX
        pts_2d.push_back ( keypoints_2[m.trainIdx].pt );
    }

    cout<<"3d-2d pairs: "<<pts_3d.size() <<endl;

	// pts_3d:相机坐标系下的3D点
    Mat r, t;
    solvePnP ( pts_3d, pts_2d, K, Mat(), r, t, false ,cv::SOLVEPNP_EPNP); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS，AP3P，UPNP，P3P等方法
    Mat R;
    cv::Rodrigues ( r, R ); // r为旋转向量形式，用Rodrigues公式转换为矩阵

    cout<<"R="<<endl<<R<<endl;
    cout<<"t="<<endl<<t<<endl;
}

void find_feature_matches ( const Mat& img_1, const Mat& img_2,
                            std::vector<KeyPoint>& keypoints_1,
                            std::vector<KeyPoint>& keypoints_2,
                            std::vector< DMatch >& matches )
{
    //-- 初始化
    Mat descriptors_1, descriptors_2;
    // used in OpenCV3
    Ptr<FeatureDetector> detector = ORB::create();
    Ptr<DescriptorExtractor> descriptor = ORB::create();
    // use this if you are in OpenCV2
    // Ptr detector = FeatureDetector::create ( "ORB" );
    // Ptr descriptor = DescriptorExtractor::create ( "ORB" );
    Ptr<DescriptorMatcher> matcher  = DescriptorMatcher::create ( "BruteForce-Hamming" );
    //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect ( img_1,keypoints_1 );
    detector->detect ( img_2,keypoints_2 );

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute ( img_1, keypoints_1, descriptors_1 );
    descriptor->compute ( img_2, keypoints_2, descriptors_2 );

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector<DMatch> match;
    // BFMatcher matcher ( NORM_HAMMING );
    matcher->match ( descriptors_1, descriptors_2, match );

    //-- 第四步:匹配点对筛选
    double min_dist=10000, max_dist=0;

    //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        double dist = match[i].distance;
        if ( dist < min_dist ) min_dist = dist;
        if ( dist > max_dist ) max_dist = dist;
    }

    printf ( "-- Max dist : %f \n", max_dist );
    printf ( "-- Min dist : %f \n", min_dist );

    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        if ( match[i].distance <= max ( 2*min_dist, 30.0 ) )
        {
            matches.push_back ( match[i] );
        }
    }
}

// 归一化，将像素坐标转换到相机坐标(非齐次坐标)
Point2d pixel2cam(const Point2d& p, const Mat& K)
{
	/* // 等价
	Mat x = (Mat_(3, 1) << p.x, p.y, 1);
	x = K.inv()*x;

	return Point2d(
	x.at(0,0),x.at(1,0)
	);
	*/
	return Point2d(
		(p.x - K.at<double>(0, 2)) / K.at<double>(0, 0), // 像素坐标系->图像坐标系->相机坐标系
		(p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
	);
}