算法| Java版《剑指offer》第1-10题

1. 二维数组中的查找

1.1 题目描述

• 在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

1.2 题目分析

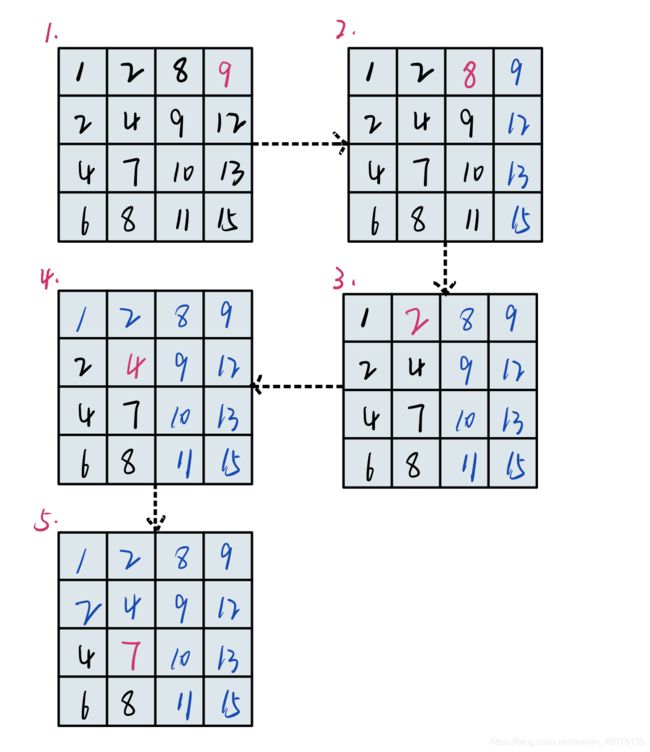
• 一个二维数组如图1

• 要查找数组7在不在数组内，我们可以选择从数组的右上角的点开始比较，此时该值为9，9>7，同时9还是第四列最小的数字，那么这意味着，第四列都不可能找到7，于是我们可以直接删除第四列。

• 蓝色代表所在的行或者列已经排查完了，红色代表当前值。此时值为8，显然和之前的结果一样，如图2。

• 然后我们比较2与7，2<7，同时2的位置是当前行内最大的数值，这意味着该行内不可能找到7，于是删除该行，如图3 。

• 4与2的情况相同，直接删除该行，如图4。

• 最后我们找到了7，如图5 。

这个思路关键的地方在于右上角点的选取，因为这个点的值是所在列的最小值和所在行的最大值，这就意味着：
要查找的数值如果比右上角的值大，那么它将大于整个行；
要查找的数值比如果右上角的值小，那么它将小于整个列。
如果相等的话，查找就结束了~~~

所以无论是哪一种情况，都可以让我们删除一个行或一个列，下一次要比较的那个值就是删除后的二维数组的右上角的值，总之永远在用右上角的值在比较。

这个一个最大一个最小的特性，**除了右上角的点之外，左下角也是满足的 **。

1.3 题目代码

public class Solution {
    public boolean Find(int target, int [][] array) {
        int row = 0;
        int cols = array[0].length - 1;
        while(row <= array.length-1 && cols >= 0){
            if(array[row][cols] == target){
                return true;
            }else if(target < array[row][cols]){
                cols--;
            }else{
                row++;
            }
        }
    return false;
    }
}

2. 替换空格

2.1 题目描述

• 请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为

  We%20Are%20Happy。

2.2 题目分析

• 先将String字符串转换为Char 数组，遍历一遍char数组统计出字符串中空格的总长度，因每次替换一个空格长度+2；故所需的总长度为
  lenth + Count * 2。

2.3 题目代码

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param s string字符串 
     * @return string字符串
     */
    public String replaceSpace (String s) {
        // write code here
        char[] chars =s.toCharArray();
        int length =chars.length;
        int count = 0;
        for(char c : chars){
            if(c == ' '){
                count++;
            }
        }
        
        char[] res = new char[length + 2*count];
        int j = 0;
        for(int i = 0;i < length; i++){
            if(chars[i] == ' ' ){
                res[j] = '%';
                res[j+1] = '2';
                res[j+2] = '0';
                j = j + 3;
            }else{
            res[j] = chars[i];
            j++;
        }
    }
                return new String(res);  
  }
}

3. 从尾到头打印链表

3.1 题目描述

• 输入一个链表，按链表从尾到头的顺序返回一个ArrayList。

3.2 题目分析

这个题目可以有三种做法：

• 1）使用用栈基于循环实现
• 2）使用递归实现
  本质也是一个栈结构，要实现反过来输出链表，我们每访问到一个节点的时候，先递归输出它后面的节点，再输出该节点本身，这样链表的输出结果就反过来了。
• 3）存储到数组或者其他容器，然后倒着遍历（不推荐）
  这里主要利用栈和使用递归实现两种方式：具体代码如下

3.3 题目代码

3.3.1 用栈基于循环实现

/**
*    public class ListNode {
*        int val;
*        ListNode next = null;
*
*        ListNode(int val) {
*            this.val = val;
*        }
*    }
*
*/
import java.util.ArrayList;
import java.util.Stack;
public class Solution {
	//1.用栈基于循环实现
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        Stack<Integer> stack =new Stack<Integer>();
        while(listNode != null){
            stack.add(listNode.val);
            listNode = listNode.next;
        }
        
        ArrayList<Integer> res =new ArrayList<Integer>();
        while(!stack.isEmpty()){
            res.add(stack.pop());
        }
        
        return res;
    }
}

3.3.2 递归方法实现

/**
 *    public class ListNode {
 *        int val;
 *        ListNode next = null;
 *  *        ListNode(int val) {
 *            this.val = val;
 *        }
 *    }
 * */
import java.util.ArrayList;
import java.util.Stack;
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
    //2.利用递归实现
        ArrayList<Integer> res = new ArrayList<Integer>();
        if(listNode != null){
               res.addAll(printListFromTailToHead(listNode.next));
               res.add(listNode.val);
            }
    return res;
    }
}

4. 重建二叉树

4.1 题目描述

• 输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

4.2 题目分析

根据中序遍历和前序遍历可以确定二叉树，具体过程为：

• 根据前序序列第一个结点确定根结点

• 根据根结点在中序序列中的位置分割出左右两个子序列

• 对左子树和右子树分别递归使用同样的方法继续分解

例如： 前序序列{1,2,4,7,3,5,6,8} = pre 中序序列{4,7,2,1,5,3,8,6} = in

• 根据当前前序序列的第一个结点确定根结点，为 1

• 找到 1 在中序遍历序列中的位置，为 in[3]

• 切割左右子树，则 in[3] 前面的为左子树， in[3] 后面的为右子树

• 则切割后的左子树前序序列为：{2,4,7}，切割后的左子树中序序列为：{4,7,2}；切割后的右子树前序序列为：{3,5,6,8}，切割后的右子树中序序列为：{5,3,8,6}

• 对子树分别使用同样的方法分解

  补充

二叉树的遍历分成三种，按照根节点的访问先后分为：
先序遍历（先根遍历）：先访问根节点，然后访问左子树， 最后访问右子树。
中序遍历（中根遍历）：先访问左子树，然后访问根节点， 最后访问右子树。
后续遍历（后根遍历）：先访问左子树，然后访问右子树，最后访问根节点。

• 先序，后序遍历可以确定根节点。
• 中序遍历可以确定左子树和右子树。

4.3 题目代码

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.util.Arrays;
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
         //递归调用的终止条件
        if(pre.length == 0 || in.length == 0){
            return null;
        }
        //由前序遍历得到该二叉树的根结点
        TreeNode root =new TreeNode(pre[0]);
        //在中序遍历中找根结点位置，进行左右子树的划分
        for(int i =0;i< in.length ;i++){
            if(in[i] == pre[0]){
                //将左子树看成一棵二叉树调用该方法，可以得到左子树根结点，即上面根结点的左子结点
                //copyOfRange(original,int from,int to)该方法返回一个长度为to-from的数组

                root.left = reConstructBinaryTree(Arrays.copyOfRange(pre,1,i+1),Arrays.copyOfRange(in,0,i));
                //将右子树看成一棵二叉树调用该方法，可以得到右子树根结点，即上面根结点的右子结点
                root.right = reConstructBinaryTree(Arrays.copyOfRange(pre,i+1,pre.length),Arrays.copyOfRange(in,i+1,in.length));
                //找到根结点位置便跳出循环
                break;
            }
        }
        return root;
    }
}

5. 用两个栈实现队列

5.1 题目描述

• 用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

5.2 题目分析

队列的特性是：“先入先出”，栈的特性是：“先入后出”

当我们向模拟的队列插入数 a,b,c 时，假设插入的是 stack1，此时的栈情况为：

• 栈 stack1：{a,b,c}
• 栈 stack2：{}

当需要弹出一个数，根据队列的"先进先出"原则，a 先进入，则 a 应该先弹出。但是此时 a 在 stack1 的最下面，将 stack1 中全部元素逐个弹出压入 stack2，现在可以正确的从 stack2 中弹出 a，此时的栈情况为：

• 栈 stack1：{}

• 栈 stack2：{c,b}

继续弹出一个数，b 比 c 先进入"队列"，b 弹出，注意此时 b 在 stack2 的栈顶，可直接弹出，此时的栈情况为：

• 栈 stack1：{}

• 栈 stack2：{c}

此时向模拟队列插入一个数 d，还是插入 stack1，此时的栈情况：

• 栈 stack1：{d}

• 栈 stack2：{c}

弹出一个数，c 比 d 先进入，c 弹出，注意此时 c 在 stack2 的栈顶，可直接弹出，此时的栈情况为：

• 栈 stack1：{d}

• 栈 stack2：{}

此时，stack2为空，stack1中的数字全部压入stack2中，此时栈的情况为：

• 栈 stack1：{}

• 栈 stack2：{d}

此时，stack2不为空，直接弹出。

根据上述例子可得出结论：

• 当插入时，直接插入 stack1

• 当弹出时，当 stack2 不为空，弹出 stack2 栈顶元素，如果 stack2 为空，将 stack1 中的全部数逐个出栈入栈
  stack2，再弹出 stack2 栈顶元素

5.3 题目代码

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
        
    }
    
    public int pop() {
        Integer a=null;
            //如果栈2不是空的，那么把最上面那个取出来
        if(!stack2.empty()){
            a=stack2.pop();
        }else{
            //如果栈2是空的，就把栈1里的数一个个取出来，放到栈2里
            while(!stack1.empty()){
                stack2.push(stack1.pop());
            }
            //栈2里有数之后，再次把里面的数取出来
            if(!stack2.empty()){
                a=stack2.pop();
            }
        }
        return a;
    }
}

6. 旋转数组的最小数字

6.1 题目描述

• 把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。

• NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

6.2 题目分析

6.3 题目代码

import java.util.ArrayList;
public class Solution {
    public int minNumberInRotateArray(int [] array) {
        if(array.length == 0){
            return 0;
        }
        int left = 0;
        int right = array.length - 1;
        while(left < right){
            int mid = (left + right) >> 1;
            if (array[mid] <= array[right]){
                right = mid;
            }else if(array[mid] >= array[right]){
                left = mid+1;
            }
        }
    return array[right];
    }
}

7. 用两个栈实现队列

7.1 题目描述

• 大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0，第1项是1）。(每种方法的分析均写到代码前的注释一行)
• n≤39

7.2 题目分析

斐波那契数列的标准公式为：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）

• 递归法：

  原理： 把 f(n) 问题的计算拆分成 f(n−1) 和 f(n−2)两个子问题的计算，并递归，以 f(0) 和 f(1) 为终止条件。
  缺点： 大量重复的递归计算，例如 f(n) 和 f(n−1) 两者向下递归都需要计算 f(n−2)的值。

• 记忆化递归法：

  原理： 在递归法的基础上，新建一个长度为 nnn 的数组，用于在递归时存储 f(0)至 f(n)的数字值，重复遇到某数字时则直接从数组取用，避免了重复的递归计算。
  缺点： 记忆化存储的数组需要使用 O(N) 的额外空间。

• 动态规划：

  原理： 以斐波那契数列性质 f(n+1)=f(n)+f(n−1)为转移方程。
  从计算效率、空间复杂度上看，动态规划是本题的最佳解法。

7.3 题目代码

7.3.1 普通递归法

public class Solution {
    public int Fibonacci(int n) {
        if(n <= 1){
            return n;
        }
        return Fibonacci(n-1) + Fibonacci(n-2);

    }
}

7.3.2 记忆化递归法

//递归会重复计算大量相同数据，我们用个数组把结果存起来
public class Solution {
    public int Fibonacci(int n) {
        int ans[] = new int[40];
        ans[0] = 0;
        ans[1] = 1;
        for(int i = 2;i<= n;i++){
            ans[i] = ans[i-1]+ans[i-2];
        }
        return ans[n];
    }
}

7.3.3 动态规划法

//其实我们可以发现每次就用到了最近的两个数，
//所以我们可以只存储最近的两个数
public class Solution {
    public int Fibonacci(int n) {
        if(n==0){
            return 0;
        }else if(n==1){
            return 1;
        }
        int sum = 0;//用于存储当前所求的数
        int one = 1;//存储第 n-1 项的值 
        int two = 0;//存储第 n-2 项的值
        for(int i = 2 ; i<=n ;i++){
            sum = one + two;
            two = one;//先把之前的one值赋给two
            one = sum;//再把新的sum值赋给one
        }
        return sum;
    }
}

7.3.4 动态规划的持续优化

/**
上一版发现，sum 只在每次计算第 n 项的时候用一下，其实还可以利用 sum 存储第 n-1 项，
例如当计算完 f(5) 时 sum 存储的是 f(5) 的值，当需要计算 f(6) 时，f(6) = f(5) + f(4)，
sum 存储的 f(5)，f(4) 存储在 one 中，由 f(5)-f(3) 得到
*/
public class Solution {
    public int Fibonacci(int n) {
        if(n==0){
            return 0;
        }else if(n==1){
            return 1;
        }
        int sum = 1;//用于存储当前所求的数 并且可以当作下一个值的前一项，即n-1项
        int one = 0;//存储第 n-2 项的值 
        for(int i = 2 ; i<=n ;i++){
            sum = sum + one;
            one = sum - one;//one值就是原来的sum值
        }
        return sum;
    }
}

8. 跳台阶

8.1 题目描述

• 大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0，第1项是1）。(每种方法的分析均写到代码前的注释一行)
• n≤39

8.2 题目分析

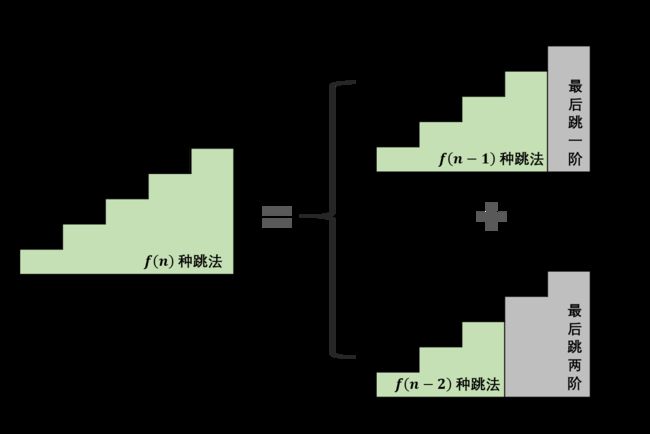
设跳上 n级台阶有 f(n) 种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上 1 级或 2 级台阶。

• 当为 1级台阶： 剩 n−1 个台阶，此情况共有 f(n−1) 种跳法；
• 当为 2级台阶： 剩 n−2 个台阶，此情况共有 f(n−2) 种跳法。

f(n)为以上两种情况之和，即 f(n)=f(n−1)+f(n−2)，以上递推性质为斐波那契数列。本题可转化为 求斐波那契数列第 n项的值 ，与 面试题斐波那契数列 等价，唯一的不同在于起始数字不同。

• 青蛙跳台阶问题： f(0)=1 , f(1)=1, f(2)=2

• 斐波那契数列问题： f(0)=0 , f(1)=1 , f(2)=1 。
  本题使用动态规划法求解：

• 大数越界:随着 target 增大, f(n) 会超过 Int32 甚至 Int64 的取值范围，导致最终的返回值错误。

8.3 题目代码

public class Solution {
    public int JumpFloor(int target) {
        if(target <= 1){
            return 1;
        }
        int two = 1;
        int one = 1,sum = 0;
        for(int i = 2 ; i <= target ;i++){
        // 大数越界:随着 target 增大, f(n) 会超过 Int32 甚至 Int64 的取值范围，导致最终的返回值错误。
            sum = (one + two)% 1000000007;
        //在leetCode中% 1000000007 防止溢出，当target>=44时，会出现溢出
            two = one;
            one = sum;
        }
        return sum;

    }
}

9. 变态跳台阶

9.1 题目描述

• 大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0，第1项是1）。(每种方法的分析均写到代码前的注释一行)
• n≤39

9.2 题目分析

设跳上 n级台阶有 f(n) 种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上 1 级或 2 级台阶。

• 当为 1级台阶： 剩 n−1 个台阶，此情况共有 f(n−1) 种跳法；
• 当为 2级台阶： 剩 n−2 个台阶，此情况共有 f(n−2) 种跳法。

f(n)为以上两种情况之和，即 f(n)=f(n−1)+f(n−2)，以上递推性质为斐波那契数列。本题可转化为 求斐波那契数列第 n项的值 ，与 面试题斐波那契数列 等价，唯一的不同在于起始数字不同。

• 青蛙跳台阶问题： f(0)=1 , f(1)=1, f(2)=2

• 斐波那契数列问题： f(0)=0 , f(1)=1 , f(2)=1 。
  本题使用动态规划法求解：

• 大数越界:随着 target 增大, f(n) 会超过 Int32 甚至 Int64 的取值范围，导致最终的返回值错误。

8.3 题目代码