一种基于灰度映射以及直方图规定化的遥感图像对比度增强技术研究
目录
- 一、绪论
- 二、基于灰度映射的对比度增强技术
-
- 2.1 线性映射
- 2.2 动态范围压缩
- 2.3 Gamma校正
- 2.4 对比度增强实例分析
- 三、基于直方图的对比度增强技术
-
- 3.1 直方图均衡化
- 3.2 直方图规定化
- 3.3 结果分析
一、绪论
遥感图像增强是遥感数字图像处理的基本内容,其目的是对遥感图像进行加工,使得对遥感图像解译来说,视觉效果更“好”、更易判读,突出遥感图像中的某些信息,削弱或除去某些不需要的信息。图像增强的主要内容是对比度增强和图像锐化。目前常用的增强技术根据其处理所进行的空间不同,可分为基于空域的方法和基于频域的方法两类。
在图像处理中,空域是指由像素组成的空间,也叫做图像域。空域增强方法指直接作用于像素改变其特性的增强方法。具体的增强操作可仅定义在每个像素位置上,此时称为“点”操作;增强操作还可以定义在每个(x,y)的某个邻域上,此时常称为模板操作和邻域操作。点操作可通过逐一将原始图像在(x,y)处灰度f映射到新灰度g来实现,也可以通过对图像或一系列图像的运算来实现,还可以借助对原始图像的某种统计进行修正来实现。而模板操作则主要通过设计模板参数来实现不同的增强操作。
在频域空间的增强是通过改变图像中不同频率分量来实现。图像频谱给出了图像全局的性质,所以频域增强不是逐个像素进行。它的基本原理是让图像在频域某个范围内的分量受到抑制而让其他分量不受影响,从而改变输出图的频率分布,达到增强的目的。
本博文从三个不同的角度介绍对遥感图像的增强:
① 通过改变图像像素的灰度分布达到图像的增强目的,采用的方法是灰度映射和直方图修正的方法;
② 依照遥感图像地物反射率及大气透射原理,采用去雾算法纠正雾霭等因素造成的图像对比度下降;
③ 通过对图像中特定频率的控制,突出图像中感兴趣的特征。
二、基于灰度映射的对比度增强技术
灰度映射可按如下函数进行描述
y = T ( x ) y=T(x) y=T(x)
即借助函数T(x)映射将原始图像中每个像素的灰度映射到新的灰度,如原来的灰度值A被映射成C,而原来的灰度值B被映射为D,如图1所示。灰度映射的意义在于通过改变图像的灰度分布,扩展图像的对比度,使图像特征变得明显,它分为线性映射和非线性映射。常见的线性映射类型有图像求反、线性拉伸和分段线性拉伸;常见的非线性映射为借助对数形式映射的动态范围压缩、借助指数形式的Gamma校正。

2.1 线性映射
改变图像灰度对比度常用的方法是线性变换,它对像素值x按以下线性变换实现一对映射:
y = a x + b y=ax+b y=ax+b
其中有参数a和b,因而至少需要提供输入图像和目标图像的两个对应灰度值才能估计得到所需要的参数。
2.2 动态范围压缩
实际应用中,有时原图的动态范围太大,超出了某些显示设备的允许范围。如果直接使用原图进行显示,则原图中低灰度的细节可能会丢失而无法显示出来。解决的办法是对原图进行灰度压缩,常用的压缩方法是借助对数形式的映射函数:
y = C × log ( 1 + ∣ x ∣ ) y=C\times \log (1+\left| x \right|) y=C×log(1+∣x∣)
其中,C为尺度比例常数,变换后原来动态范围很大的x会转换为动态范围很小的y。低灰度之经过映射后,其灰度值会集中在高亮度区域,这时只需显示动态范围较小的高亮度区域就可以把大部分的图像细节展示出来。
2.3 Gamma校正
Gamma曲线是一种特殊的色调曲线,当Gamma值等于1的时候,曲线为与坐标轴成45°的直线,这个时候表示输入和输出密度相同。一般情况下,当用于Gamma校正的值大于1时,图像的高光部分被压缩而暗调部分被扩展,当Gamma校正的值小于1时,图像的高光部分被扩展而暗调部分被压缩,Gamma校正一般用于平滑的扩展暗调的细节。在显示器、扫描仪、打印机等输入、输出设备中这是一个相当常见并且比较重要的概念。在计算机系统中,由于显卡或者显示器的原因会出现实际输出的图像在亮度上有偏差,而Gamma曲线校正就是通过一定的方法来校正图像的这种偏差的方法。如图2所示的实线为 γ = 2.2 \gamma =2.2 γ=2.2 ,虚线为 γ = 1 / 2.2 \gamma ={1}/{2.2}\; γ=1/2.2 。
y = 255 ∗ ( x 255 ) γ y=255*{{\left( \frac{x}{255} \right)}^{\gamma }} y=255∗(255x)γ
2.4 对比度增强实例分析
基于对比度受约束的自适应直方图均衡增强Contrast-limited Adaptive Histogram Equalization (CLAHE)结果如下图所示

三、基于直方图的对比度增强技术
直方图是对图像的一种抽象形式,借助它对图像的修改或变换可以改变图像像素的灰度分布,从而达到对图像进行增强的目的。常用的方法主要有直方图均衡化和直方图规定化。
图像的直方图是一个1-D的离散函数,可写成
h ( f k ) = n k , k = 0 , 1 , ⋯ , L − 1 h\left( {{f}_{k}} \right)={{n}_{k}},k=0,1,\cdots ,L-1 h(fk)=nk,k=0,1,⋯,L−1
这里 n k {{n}_{k}} nk是图像f(x,y)中具有灰度值 f k {{f}_{k}} fk的像素个数,将其写成一般的概率表达式为:
P ( f k ) = n k , k = 0 , 1 , ⋯ , L − 1 P\left( {{f}_{k}} \right)={{n}_{k}},k=0,1,\cdots ,L-1 P(fk)=nk,k=0,1,⋯,L−1
这里n是图像中像素的总个数。直方图提供了原图中灰度值的分布情况,也可以说给出了对一幅图像所有灰度值的整体描述。图像的视觉效果和其直方图有对应的关系,或者说直方图的形状和改变对图像有很大的影响。
图像的累积直方图也是一个1-D的离散函数,可写成:
C ( f k ) = ∑ k = 1 L − 1 n k , k = 0 , 1 , ⋯ , L − 1 C\left( {{f}_{k}} \right)=\sum\limits_{k=1}^{L-1}{{{n}_{k}},k=0,1,\cdots ,L-1} C(fk)=k=1∑L−1nk,k=0,1,⋯,L−1
累计直方图中列k的高度给出了灰度值小于和等于 f k {{f}_{k}} fk的像素的总个数,写成概率的形式是:
C ( f k ) = ∑ k = 1 L − 1 n k / n = ∑ k = 1 L − 1 P k , k = 0 , 1 , ⋯ , L − 1 C\left( {{f}_{k}} \right)=\sum\limits_{k=1}^{L-1}{{{{n}_{k}}}/{n}\;=\sum\limits_{k=1}^{L-1}{{{P}_{k}}},k=0,1,\cdots ,L-1} C(fk)=k=1∑L−1nk/n=k=1∑L−1Pk,k=0,1,⋯,L−1
3.1 直方图均衡化
直方图均衡化的基本思想是把原始图像的直方图变换成均匀分布的形式,这样就增加了图像灰度值的动态范围,从而达到了增强图像整体对比度的效果。这种变换可由图像的累积直方图得到。
具体方法是:
第一步 列出原始图像的灰度级 s k , k = 0 , 1 , ⋯ , L − 1 {{s}_{k}},k=0,1,\cdots ,L-1 sk,k=0,1,⋯,L−1,其中L是灰度级的个数;
第二步 统计原始图像中各灰度级的像素数目 n k {{n}_{k}} nk;
第三步 计算原始图像直方图各灰度级的频率数;
第四步 计算原始图像的累计直方图;
第五步 取整计算 g k = int [ ( L − 1 ) × C ( f k ) + 0.5 ] {{g}_{k}}=\operatorname{int}\left[ \left( L-1 \right)\times C\left( {{f}_{k}} \right)+0.5 \right] gk=int[(L−1)×C(fk)+0.5];
第六步 确定映射关系 f k = g k {{f}_{k}}={{g}_{k}} fk=gk;
第七步 统计新直方图各个灰度级的像素值;
第八步 计算新的直方图。
3.2 直方图规定化
直方图均衡化的优点是能够自动增强整个图像的对比度,但计算过程中因没有用户可以调整的参数而不易控制,处理的结果总是得到全局均衡化的直方图。实际应用中有时需要修正直方图使其变成规定形状的直方图,从而可以有选择地增强某个灰度值范围的对比度,这时可以采用比较灵活的直方图规定化方法。直方图规定化主要有三个步骤:
第一步 如同均衡化一样,对原始图的直方图进行灰度均衡化:
C ( f k ) = ∑ i = 1 L − 1 n i / n = ∑ i = 0 L − 1 P i , i = 0 , 1 , ⋯ , L − 1 C\left( {{f}_{k}} \right)=\sum\limits_{i=1}^{L-1}{{{{n}_{i}}}/{n}\;=\sum\limits_{i=0}^{L-1}{{{P}_{i}}},i=0,1,\cdots ,L-1} C(fk)=i=1∑L−1ni/n=i=0∑L−1Pi,i=0,1,⋯,L−1
第二步 规定需要的直方图,并计算能使规定的直方图均衡化的变换:
C ( t j ) = ∑ j = 0 N − 1 n j / n = ∑ j = 0 N − 1 P j , j = 0 , 1 , ⋯ , L − 1 C\left( {{t}_{j}} \right)=\sum\limits_{j=0}^{N-1}{{{{n}_{j}}}/{n}\;=\sum\limits_{j=0}^{N-1}{{{P}_{j}}},j=0,1,\cdots ,L-1} C(tj)=j=0∑N−1nj/n=j=0∑N−1Pj,j=0,1,⋯,L−1
第三步 将第一步所得的变换反转过来,即使原始直方图对应映射到规定的直方图,也就是将 P i {{P}_{i}} Pi对应映射到 P j {{P}_{j}} Pj来,映射方法有单映射和组映射。
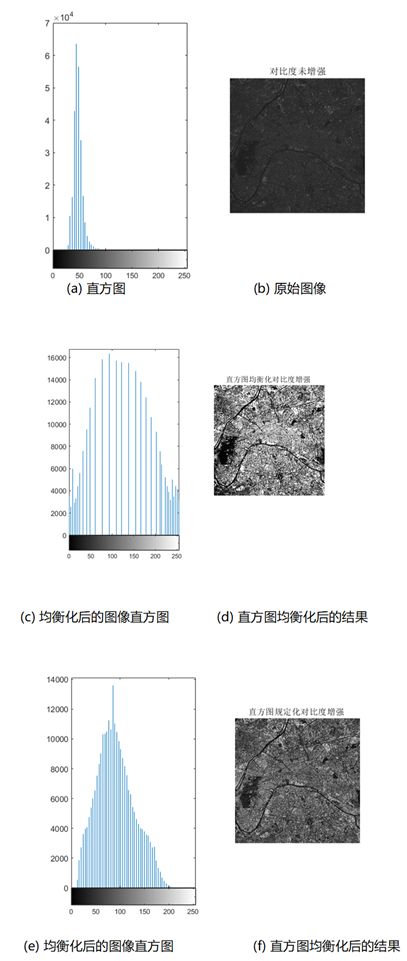
3.3 结果分析
结果表明,直方图显示它们的灰度范围较窄,因而图像的对比度差,而随着对比度逐渐增强后,直方图灰度范围逐渐变宽。实验结果显示直方图归一化是一个非常有用的对比度增强工具。
博主简介:擅长智能优化算法、信号处理、图像处理、机器视觉、神经网络等领域Matlab仿真以及实验数据分析等,matlab代码问题、程序获取、课题选题与指导等均可私信交流。