数学建模-回归分析(Stata)
注意:代码文件仅供参考,一定不要直接用于自己的数模论文中
国赛对于论文的查重要求非常严格,代码雷同也算作抄袭
如何修改代码避免查重的方法:https://www.bilibili.com/video/av59423231 //清风数学建模
一、基础知识
1.简介
X是自变量,Y是因变量。目的是通过X去预测Y。
一般处理模型像:期末成绩分析,Y是成绩,X是性别、是否是班干部、平时作业完成度等自变量。银行借贷成功率分析等问题。
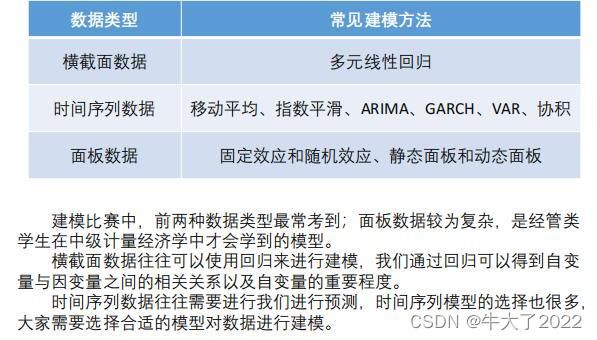
2.不同数据类型的处理方法
3.一元线性回归
①扰动项u与x均不相干,模型有外生性;否则存在内生性。包含了所有与y相关,但未添加到回归模型中的变量,如果这些变量和我们已经添加的自变量相关,则存在内生性。
②内生性的蒙特卡罗模拟:
%% 蒙特卡洛模拟:内生性会造成回归系数的巨大误差
times = 300; % 蒙特卡洛的次数
R = zeros(times,1); % 用来储存扰动项u和x1的相关系数
K = zeros(times,1); % 用来储存遗漏了x2之后,只用y对x1回归得到的回归系数
for i = 1: times
n = 30; % 样本数据量为n
x1 = -10+rand(n,1)*20; % x1在-10和10上均匀分布,大小为30*1
u1 = normrnd(0,5,n,1) - rand(n,1); % 随机生成一组随机数
x2 = 0.3*x1 + u1; % x2与x1的相关性不确定, 因为我们设定了x2要加上u1这个随机数
% 这里的系数0.3我随便给的,没特殊的意义,你也可以改成其他的测试。
u = normrnd(0,1,n,1); % 扰动项u服从标准正态分布
y = 0.5 + 2 * x1 + 5 * x2 + u ; % 构造y
k = (n*sum(x1.*y)-sum(x1)*sum(y))/(n*sum(x1.*x1)-sum(x1)*sum(x1)); % y = k*x1+b 回归估计出来的k
K(i) = k;
u = 5 * x2 + u; % 因为我们回归中忽略了5*x2,所以扰动项要加上5*x2
r = corrcoef(x1,u); % 2*2的相关系数矩阵
R(i) = r(2,1);
end
plot(R,K,'*')
xlabel("x_1和u'的相关系数")
ylabel("k的估计值")③主要证明:核心变量与u不相干
核心解释变量: 我们最感兴趣的变量,因此我们特别希望得到对其系数的一致估计(当样本容量无限增大时,收敛于待估计参数的真值 )。控制变量: 我们可能对于这些变量本身并无太大兴趣;而之所以把它们也放入回归方程,主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素。
④什么时候取对数
对于什么时候取对数还没有固定的规则,但是有一些经验法则:(1)与市场价值相关的,例如,价格、销售额、工资等都可以取对数;(2)以年度量的变量,如受教育年限、工作经历等通常不取对数;(3)比例变量,如失业率、参与率等,两者均可;(4)变量取值必须是非负数,如果包含0,则可以对y取对数ln(1+y);取对数的好处: (1)减弱数据的异方差性(2)如果变量本身不符合正态分布,取了对数后 可能渐近服从正态分布(3)模型形式的需要,让模型具有经济学意义。
⑤三(四)种模型
1 、 一元线性回归 : = + + , x 每增加 1 个单位, y 平均变化 b 个单位;2 、 双对数模型 : = + + , x 每增加 1% , y 平均变化 b% ;3 、 半对数模型 : = + + , x 每增加 1% , y 平均变化 b/100 个单位;4 、 半对数模型 := + + , x 每增加 1 个单位, y 平均变化 (100b)% 。
⑥自变量有定性变量(如男女)引入虚拟变量x(女x=1 男x=0)
二、实战演练(Stata)
1.题目
打卡stata导入,勾上第一个
2.定量数据和定性数据
定性数据是与描述有关的数据,可以观察到但无法计算。 相反,定量数据是一个专注于数字和数学计算,可以计算和计算的。
比如数据中价格、评价量和重量都是可以拿数字直接表示,而产品名产地这种无法计算的只能定性处理。
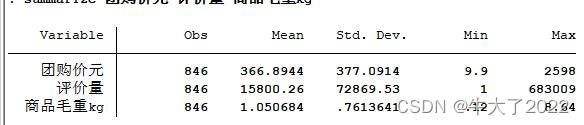
summarize 团购价元 评价量 商品毛重kg评价变量,想评价啥就输入评价量
// 定性变量的频数分布,并得到相应字母开头的虚拟变量
tabulate 配方,gen(A)
tabulate 奶源产地 ,gen(B)
tabulate 国产或进口 ,gen(C)
tabulate 适用年龄岁 ,gen(D)
tabulate 包装单位 ,gen(E)
tabulate 分类 ,gen(F)
tabulate 段位 ,gen(G)之后右侧会生成A1A2A3B1B2等变量
3.回归(默认OLS:普通最小二乘估计法)
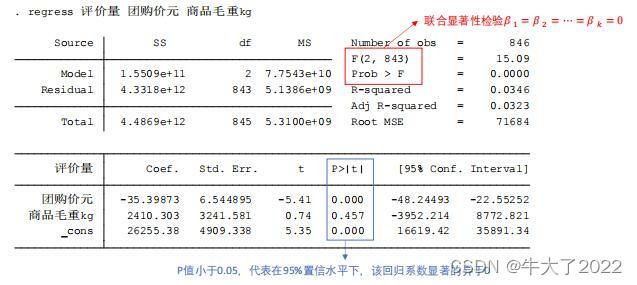
regress y x1 x2 … xkregress 评价量 团购价元 商品毛重 kg
加入虚拟变量回归
小技巧全选:鼠标在右边变量框下滑选中最后一个点击(文章是G4),再shift点击第一个即可全选,复制即可得到所有变量名。
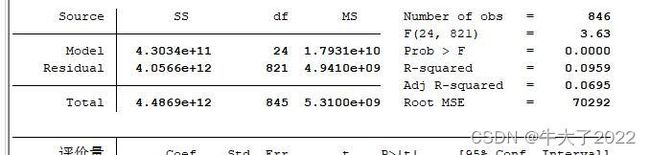
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
注意只要定量变量+字母的定性变量
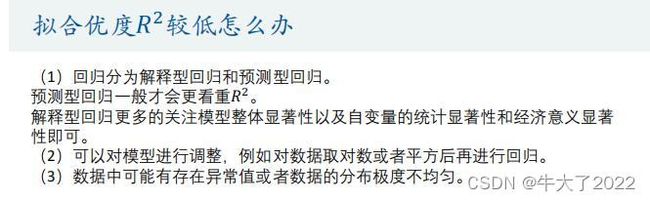
上图的R-squared即R方,越高越好。
4.标准化回归系数
regress y x1 x2 … xk,betaregress 评价量 团购价元 商品毛重kg,b
5.拓展
1.异方差;
横截面数据容易出现异方差的问题,时间序列数据容易出现自相关的问题。
异方差的检验:
在回归结束后运行命令:rvfplot (画残差与拟合值的散点图)rvpplot x ( 画残差与自变量 x 的散点图 )
2.拟合值出现负数的原因
3.异方差的假设检验
BP法
Stata 命令(在回归结束后使用):estat hettest ,rhs iid
怀特检验原假设:不存在异方差Stata 命令(在回归结束后使用):estat imtest,white
4.处理异方差
使用OLS + 稳健的标准误
regress y x1 x2 … xk,robust5.检验多重共线性
(vif>10认为存在严重的多重共线性)
Stata计算各自变量VIF的命令(在回归结束后使用):
estat vif6. 逐步回归分析
向前逐步回归Forward selection:
stepwise regress y x1 x2 … xk, pe(#1)
(显著才加入模型中).
向后逐步回归Backward elimination:
stepwise regress y x1 x2 … xk, pr(#2)
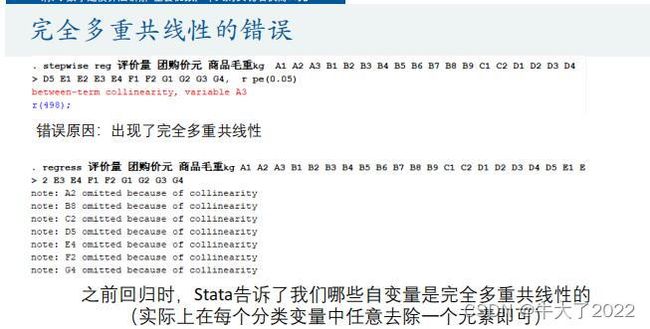
(不显著就剔除出模型).stepwise reg 评价量 团购价元 商品毛重 kg A1 A3 B1 B2 B3 B4 B5B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r pe(0.05)