迁移学习——A Tutorial on Principal Component Analysis

《A Tutorial on Principal Component Analysis》学习
arXiv

---

摘要

这个手稿集中在建立一个坚实的直觉如何和为什么主成分分析工作。这手稿结晶这一知识从简单的直觉，背后的数学PCA。本教程不回避非正式地解释思想，也不回避数学。我们希望通过解决这两个方面的问题，各级读者将能够更好地理解PCA，以及何时、如何和为什么应用这种技术。

一、介绍

主成分分析(PCA)是现代数据分析的标准工具——在从神经科学到计算机图形学的不同领域——因为它是一种简单的、非参数的方法，可以从混乱的数据集中提取相关信息。
通过最小的努力，PCA为如何将复杂的数据集减少到更低的维度，以揭示其背后有时隐藏的、简化的结构提供了路线图。
我们将继续增加数学的严密性，把它放在线性代数的框架内，以提供一个显式的解决方案。我们将看到PCA如何以及为什么与奇异值分解(SVD)的数学技术密切相关。

二、动机:一个玩具例子

以图1中物理图中的一个简单玩具问题为例

假设我们正在研究物理学家理想弹簧的运动。这个系统由一个质量为m的球和一个无质量无摩擦的弹簧组成。球在远离平衡的一小段距离被释放(即弹簧被拉伸)。因为弹簧是理想的，它沿着x轴，以固定的频率，围绕平衡无限振荡。
潜在的动力学可以表示为一个单一变量x的函数。
具体来说，我们在我们感兴趣的系统周围放置了三个电影摄像机。在120赫兹的频率下，每个电影摄像机记录一个图像，表明球的二维位置(投影)。
不幸的是，我们甚至不知道真正的x、y和z轴是什么，所以我们选择了三个相机位置$\tilde{a},\tilde{b}和\tilde{c}$，对系统进行任意角度的选择。我们测量的角度甚至可能不是90度!
在玩具的例子中，这意味着我们需要处理空气，不完美的相机，甚至摩擦在一个不太理想的弹簧。噪声污染了我们的数据集，只会进一步混淆动态。这个玩具例子是实验者每天都要面对的挑战。

三、框架:改变基础

主成分分析的目标是找出最有意义的基础来重新表达数据集。我们希望这种新的基础能够过滤掉噪音，揭示隐藏的结构。

3.1一个原始的基础

在我们的数据集中，在某一时刻，摄像机A记录了一个相应的球的位置$(x_A,y_A)$。一个样本或试验可以表示为6维列向量
$$X=\left[\begin{array}{c}{x}_A\\ y_A\\ x_B\\ y_B\\ x_C\\ y_C\end{array}\right]$$
其中，每个摄像机贡献了一个球的位置到整个矢量$X$的二维投影。如果我们以120赫兹的频率记录球的位置10分钟，
那么我们就记录了$10\times 60\times 120=72000$个矢量。

我们的原始基础反映了我们测量数据的方法。

我们如何在线性代数中表达这个朴素的基?在二维情况下，$\{(1,0)，(0,1)\}$可以被重铸为单独的行向量。由这些行向量构成的矩阵是$2\times 2$单位矩阵$\mathbf{I}$
我们可以通过构造$m\times m$单位矩阵来推广到m维的情况
$$\mathbf{B}=\left[\begin{array}{c}{\mathbf{b}}_1\\ {\mathbf{b}}_2\\ ⋮\\ {\mathbf{b}}_m\end{array}\right]=\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right]=\mathbf{I}$$
其中每一行是正交基向量${\mathbf{b}}_i$，有m个分量。我们可以把朴素的基础作为有效的起点。我们所有的数据都是在这个基础上记录的，因此它可以简单地表示为$\{{\mathbf{b}}_i\}$的线性组合。

3.2基底

有了这种严谨，我们现在可以更精确地表述PCA所问的问题:是否存在另一种基，即原始基的线性组合，可以最好地重新表达我们的数据集?
事实上，PCA做出了一个严格但强大的假设:线性。线性通过限制潜在基的集合极大地简化了问题。有了这个假设，PCA现在被限制为将数据重新表示为其基向量的线性组合。
设X为原始数据集，其中每一列为我们的数据集(即$\tilde{X}$)的单个样本(或时刻)。在玩具的例子中，X是一个m × n矩阵，其中m = 6, n = 72000。
设Y是另一个与线性变换p相关的m × n矩阵，X是原始记录数据集，Y是该数据集的新表示。
$$\mathbf{PX}=\mathbf{Y}\text{\hspace{1em}(1)}$$
让我们定义下面的量。

1. ${\mathbf{p}}_i$是$\mathbf{P}$的行
2. ${\mathbf{x}}_i$是$\mathbf{X}$的列(或单独的$X$)
3. ${\mathbf{y}}_i$是$\mathbf{Y}$的列向量。

方程式1表示基的变化，因此可以有多种解释。

1. $\mathbf{P}$是一个将X转换为Y的矩阵。
2. 几何上，$\mathbf{P}$是旋转和拉伸，将$\mathbf{X}$再次转换为$\mathbf{Y}$
3. $\mathbf{P}，\{{\mathbf{p}}_1，\dots ，{\mathbf{p}}_m\}，$是一组新的基向量，用来表示$\mathbf{X}$的列。

后一种解释不明显，但可以通过写出$\mathbf{PX}$的显式点积看出。
$$\begin{gathered} \mathbf{PX}=\left[\begin{array}{c}{\mathbf{p}}_1\\ ⋮\\ {\mathbf{p}}_m\end{array}\right]\left[\begin{array}{ccc}{\mathbf{x}}_1& \cdots & {\mathbf{x}}_n\end{array}\right] \\ \mathbf{Y}=\left[\begin{array}{ccc}{\mathbf{p}}_1\cdot {\mathbf{x}}_1& \cdots & {\mathbf{p}}_1\cdot {\mathbf{x}}_n\\ ⋮& \ddots & ⋮\\ {\mathbf{p}}_m\cdot {\mathbf{x}}_1& \cdots & {\mathbf{p}}_m\cdot {\mathbf{x}}_n\end{array}\right] \end{gathered}$$
我们可以记下$\mathbf{Y}$每一列的形式。
$${\mathbf{y}}_i=\left[\begin{array}{c}{\mathbf{p}}_1\cdot {\mathbf{x}}_i\\ ⋮\\ {\mathbf{p}}_m\cdot {\mathbf{x}}_i\end{array}\right]$$
我们认识到${\mathbf{y}}_i$的每个系数都是${\mathbf{x}}_i$与$\mathbf{p}$中相应行的点积。换句话说，${\mathbf{y}}_i$的第$j$个系数是$\mathbf{p}$中第$j$行上的投影。这实际上是一个方程的形式，其中${\mathbf{y}}_i$是对$\{{\mathbf{p}}_1，\dots ,{\mathbf{p}}_{\mathbf{m}}\}$。因此，$\mathbf{p}$的行是一组新的基向量用来表示$\mathbf{X}$的列。

3.3剩余的问题

通过假设线性，问题可以简化为寻找适当的基底变换。行向量$\{{\mathbf{p}}_1，\dots ,{\mathbf{p}}_{\mathbf{m}}\}$将成为$\mathbf{X}$的主要组成部分。现在出现了几个问题。

1. 重新表达$\mathbf{X}$的最好方式是什么?
2. 什么是基底$\mathbf{P}$的最佳选择?

这些问题必须通过问自己我们希望Y展示什么特性来回答。显然，要得到一个合理的结果，需要额外的线性假设。

四、方差和目标

现在最重要的问题来了:什么最能表达数据的意思?

4.1噪声和旋转

任何数据集中的测量噪声必须很低，否则无论采用何种分析技术，都无法提取信号的信息。噪声不存在绝对尺度，而是所有的噪声相对于信号强度被量化。常用的度量方法是信噪比(SNR)，即方差的${\sigma }^2$，
$$SNR=\frac{{\sigma }_{signal}^2}{{\sigma }_{noise}^2}$$
高信噪比$(\gg 1)$表示测量精度高，低信噪比表示数据噪声大。
让我们仔细查看图2中摄像机a的数据。

通过假设合理良好的测量，我们定量地假设测量空间中方差最大的方向包含感兴趣的动态。在图2中，方差最大的方向不是${\hat{x}}_A=(1,0)$，也不是${\hat{y}}_A=(0,1)$，而是沿着云的长轴的方向。
因此，通过假设，兴趣动态沿方差最大、信噪比可能最高的方向存在。
最大化方差(并通过假设信噪比)对应于找到朴素基的适当旋转。这种直觉对应于找到图2中${\sigma }^2$信号所示的方向。
在图2的二维情况中，最大方差的方向对应于数据云的最佳拟合线。因此，将原始基旋转到与最佳拟合线平行的位置，就可以揭示二维情况下弹簧的运动方向。

4.2冗余

图3可能反映了两个任意测量类型r1和r2之间可能的绘图范围。

图3的右边面板描述了高度相关的记录。这种极端情况可以通过几种方法实现:

1. 如果摄像机A和B很近，图是$(x_A,x_B)$
2. 一个$(x_A，{\hat{x}}_A)$的图，其中$x_A$是在米中，${\hat{x}}_A$是在英寸中。

很明显，在图3的右侧面板中，只记录单个变量比同时记录两个变量更有意义。为什么?因为可以用最佳拟合直线从$r_2$算出$r_1$(反之亦然)。只记录一个响应可以更简洁地表达数据，减少传感器记录的数量(2→1个变量)。事实上，这就是降维背后的核心思想。

4.3协方差矩阵

在2个变量的情况下，通过找到最佳拟合线的斜率并判断拟合的质量，很容易识别冗余情况。我们如何量化这些概念并将其推广到任意更高的维度?考虑两组均值为零的度量
$$A=\{a_1,a_2,\dots ,a_n\},B=\{b_1,b_2,\dots ,b_n\}$$
式中下标为样本数。A、B的方差分别定义为:
$${\sigma }_A^2=\frac{1}{n}\sum _i{a}_i^2,{\sigma }_B^2=\frac{1}{n}\sum _i{b}_i^2$$
A和B之间的协方差是一个简单的泛化。
$$\text{covariance of A and B}\equiv {\sigma }_{AB}^2=\frac{1}{n}\sum _i{a}_i{b}_i$$
协方差衡量的是两个变量之间线性关系的程度。较大的正值表示数据正相关。同样，较大的负值表示数据为负相关。协方差的绝对值衡量的是冗余度。还有一些关于协方差的事实。

1. ${\sigma }_{AB}$当且仅当A和B不相关时(如:图2，左面板)。
2. $A=B$时，${\sigma }_{AB}^2={\sigma }_A^2$。

我们可以等价地把A和B转换成相应的行向量。
$$\begin{gathered} \mathbf{a}=[a_1{a}_2\dots a_n] \\ \mathbf{b}=[b_1{b}_2\dots b_n] \end{gathered}$$
这样我们就可以用点积矩阵的计算来表示协方差
$${\sigma }_{\mathbf{ab}}^2\equiv \frac{1}{n}{\mathbf{ab}}^T\text{\hspace{1em}(2)}$$
最后，我们可以将两个向量推广到任意数。将行向量$\mathbf{a}$和$\mathbf{b}$分别重命名为${\mathbf{x}}_1$和${\mathbf{x}}_2$，并考虑额外的索引行向量${\mathbf{x}}_3，\dots ,{\mathbf{x}}_m$。

定义一个新的$m\times n$矩阵$\mathbf{X}$。
$$\mathbf{X}=\left[\begin{array}{c}{\mathbf{x}}_1\\ ⋮\\ {\mathbf{x}}_{\mathbf{m}}\end{array}\right]$$
对$\mathbf{X}$的一种解释如下。
每一行$\mathbf{X}$对应于特定类型的所有测量值。$\mathbf{X}$的每一列对应一个特定试验的一组测量值(这是3.1节中的$X$)。现在我们得到协方差矩阵${\mathbf{C}}_{\mathbf{X}}$的定义。
$${\mathbf{C}}_{\mathbf{X}}\equiv \frac{1}{n}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$$
考虑矩阵${\mathbf{C}}_{\mathbf{X}}=\frac{1}{n}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$。${\mathbf{C}}_{\mathbf{X}}$的第i j个元素是第i个测量类型的向量与第j个测量类型的向量之间的点积。我们可以总结出${\mathbf{C}}_{\mathbf{X}}$的几个性质:

1. ${\mathbf{C}}_{\mathbf{X}}$是一个平方对称的$m\times m$矩阵(附录a的定理2)
2. ${\mathbf{C}}_{\mathbf{X}}$的对角线项是特定测量类型的方差。
3. ${\mathbf{C}}_{\mathbf{X}}$的非对角线项是测量类型之间的协方差。

${\mathbf{C}}_{\mathbf{X}}$捕获所有可能的测量对之间的协方差。协方差值反映了我们测量中的噪声和冗余。

1. 在对角线项中，通过假设，大的值对应有趣的结构。
2. 在非对角线术语中，大的幅度对应高冗余。

假设我们可以操纵${\mathbf{C}}_{\mathbf{X}}$。我们将建议定义我们的操作协方差矩阵${\mathbf{C}}_{\mathbf{Y}}$，我们想在${\mathbf{C}}_{\mathbf{Y}}$中优化什么特征?

4.4对角化协方差矩阵

我们可以通过陈述我们的目标(1)最小化冗余(通过协方差的大小衡量)和(2)最大化信号(通过方差衡量)来总结最后两个部分。优化后的协方差矩阵${\mathbf{C}}_{\mathbf{Y}}$是什么样的?

1. ${\mathbf{C}}_{\mathbf{Y}}$中所有非对角线项都应为零。因此，${\mathbf{C}}_{\mathbf{Y}}$一定是一个对角矩阵。或者换种说法，$\mathbf{Y}$是装饰相关的。
2. $\mathbf{Y}$中每个连续的维度应该根据方差进行排序。

有许多对角化 ${\mathbf{C}}_{\mathbf{Y}}$的方法，值得注意的是PCA选择了最简单的方法:PCA假设所有基向量$\{{\mathbf{p}}_1，\dots ，{\mathbf{p}}_{\mathbf{m}}\}$是正交的，即 $\mathbf{P}$是一个标准正交矩阵。为什么这个假设最简单?
设想PCA是如何工作的。在图2的简单示例中，$\mathbf{P}$充当广义旋转，使基与最大方差轴对齐。在多个维度上，这可以通过一个简单的算法来实现

1. 在m维空间中选择一个$\mathbf{X}$中方差最大的归一化方向。将这个向量保存为${\mathbf{p}}_1$。
2. 找到另一个方差最大的方向，但是，由于正交条件，限制搜索的所有方向正交于所有之前选择的方向。将这个向量保存为${\mathbf{p}}_{\mathbf{i}}$
3. 重复这个过程，直到选择m个向量

得到的$\mathbf{p}$的有序集合是主要成分。
原则上，这个简单的算法是可行的，然而，这与为什么标准正交假设是明智的真正原因不符。这种假设的真正好处是，存在一个有效的分析解决方案来解决这个问题。我们将在以下部分讨论两个解决方案
注意我们用秩序方差的规定得到了什么。我们有一个方法来判断主要方向的重要性。即，与每个方向${\mathbf{p}}_{\mathbf{i}}$相关的方差根据相应的方差对每个基向量${\mathbf{p}}_{\mathbf{i}}$进行排序，从而量化每个方向的“主”程度。

4.5总结的假设

这一节提供了一个总结的假设背后的PCA和暗示，当这些假设可能表现不佳。

1. 线性
   线性把问题框定为基的改变。一些研究领域已经探索了如何将这些概念扩展到非线性状态(见讨论)。
2. 大的方差具有重要的结构。
   这个假设还包含了数据具有高信噪比的信念。因此，相关方差较大的主成分代表有趣的结构，而方差较低的主成分代表噪声。请注意，这是一个强有力的，有时是不正确的假设(参见讨论)。
3. 主成分是正交的。
   这个假设提供了一个直观的简化，使PCA可以用线性代数分解技术进行分解。以下两部分将重点介绍这些技术。

我们已经讨论了推导PCA的所有方面-剩下的是线性代数解。第一个解决方案有些直接，而第二个解决方案涉及到理解一个重要的代数分解。

五、用特征向量分解求解主分量

基于特征向量分解的一个重要性质，我们得到了主成分分析的第一个代数解。同样，数据集是$\mathbf{X}$，一个$m\times n$的矩阵，其中m为测量类型的数量，n为样本的数量。目标总结如下
求$\mathbf{Y}=\mathbf{PX}$中的某个标准正交矩阵$\mathbf{P}$，使${\mathbf{C}}_{\mathbf{Y}}\equiv \frac{1}{n}\mathbf{Y}{\mathbf{Y}}^{\mathbf{T}}$是一个对角矩阵。$\mathbf{P}$的行是$\mathbf{X}$的主成分。
我们先把${\mathbf{C}}_{\mathbf{Y}}$写成未知变量的形式。
$$\begin{gathered} {\mathbf{C}}_{\mathbf{Y}}=\frac{1}{n}\mathbf{Y}{\mathbf{Y}}^{\mathbf{T}} \\ =\frac{1}{n}(\mathbf{PX})(\mathbf{PX}{)}^T \\ =\frac{1}{n}\mathbf{PX}{\mathbf{X}}^{\mathbf{T}}{\mathbf{P}}^{\mathbf{T}} \\ =\mathbf{P}(\frac{1}{n}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}){\mathbf{P}}^T \\ {\mathbf{C}}_{\mathbf{Y}}=\mathbf{P}{\mathbf{C}}_{\mathbf{X}}{\mathbf{P}}^{\mathbf{T}} \end{gathered}$$
注意，我们已经确定了$\mathbf{X}$的协方差矩阵在最后一行。
我们的计划是认识到任何对称矩阵$\mathbf{A}$是由其特征向量的正交矩阵对角化的(由附录A中的定理3和4)。
对于一个对称矩阵，定理4提供了$\mathbf{A}={\mathbf{EDE}}^T$，其中$\mathbf{D}$是一个对角矩阵，$\mathbf{E}$是$\mathbf{A}$的特征向量作为列排列的矩阵。
现在，关键来了。我们选择矩阵$\mathbf{P}$作为一个矩阵其中每一行${\mathbf{p}}_i$是一个特征向量为$\frac{1}{n}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$。通过这个选择，$\mathbf{P}\equiv {\mathbf{E}}^{\mathbf{T}}$。利用这个关系和附录$A({\mathbf{P}}^{-1}={\mathbf{P}}^T)$定理1，我们可以完成对${\mathbf{C}}_{\mathbf{Y}}$的求值。
$$\begin{array}{rl}{\mathbf{C}}_{\mathbf{Y}}& =\mathbf{P}{\mathbf{C}}_{\mathbf{X}}{\mathbf{P}}^{\mathbf{T}}\\ & =\mathbf{P}({\mathbf{E}}^{\mathbf{T}}\mathbf{DE}){\mathbf{P}}^T\\ & =\mathbf{P}({\mathbf{P}}^{\mathbf{T}}\mathbf{DP}){\mathbf{P}}^T\\ & =(\mathbf{P}{\mathbf{P}}^{\mathbf{T}})\mathbf{D}(\mathbf{P}{\mathbf{P}}^{\mathbf{T}})\\ & =(\mathbf{P}{\mathbf{P}}^{-1})\mathbf{D}(\mathbf{P}{\mathbf{P}}^{-1})\\ {\mathbf{C}}_{\mathbf{Y}}& =\mathbf{D}\end{array}$$
很明显，$\mathbf{P}$的选择对角化了${\mathbf{C}}_{\mathbf{Y}}$，这是PCA的目标。我们可以总结矩阵$\mathbf{P}$和${\mathbf{C}}_{\mathbf{Y}}$中主成分分析的结果。

1. $\mathbf{X}$的主分量是${\mathbf{C}}_{\mathbf{X}}=\frac{1}{n}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$的特征向量。
2. ${\mathbf{C}}_{\mathbf{Y}}$的第i个对角线值是$\mathbf{X}$沿${\mathbf{p}}_i$的方差。

在实践中，计算数据集$\mathbf{X}$的主成分分析需要

1. 减去每个测量类型的平均值和
2. 计算${\mathbf{C}}_{\mathbf{X}}$的特征向量。这个解决方案在附录B中包含的Matlab代码中进行了演示

六、使用SVD的更通用的解决方案

我们导出了主成分分析的另一种代数解，在此过程中，发现主成分分析与奇异值分解(SVD)密切相关。事实上，这两者是如此密切相关，以至于这两个名字经常被互换使用。我们将看到的是SVD是理解基的变化的更一般的方法。

6.1奇异值分解

设$\mathbf{X}$是一个任意的$n\times m$矩阵，${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$是一个秩$r$平方对称的$m\times m$矩阵。

1. $\{{\hat{\mathbf{v}}}_1，{\hat{\mathbf{v}}}_2，\dots ，{\hat{\mathbf{v}}}_r\}$是标准正交$m\times 1$特征向量的集合，其特征值为$\{{\lambda }_1，{\lambda }_2，\dots ，{\lambda }_r\}$的对称矩阵${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$。
   $$({\mathbf{X}}^T\mathbf{X}){\hat{\mathbf{v}}}_i={\lambda }_i{\hat{\mathbf{v}}}_i$$
2. ${\sigma }_i\equiv \sqrt{{\lambda }_i}$为正实，称为奇异值。
3. $\{{\hat{\mathbf{u}}}_1，{\hat{\mathbf{u}}}_2，\dots ，{\hat{\mathbf{u}}}_r\}$是${\hat{\mathbf{u}}}_i\equiv \frac{1}{{\sigma }_i}\mathbf{X}{\hat{\mathbf{v}}}_i$定义的$n\times 1$向量的集合。

最终的定义包括两个意想不到的新属性。
$${\hat{\mathbf{u}}}_{\mathbf{i}}\cdot {\hat{\mathbf{u}}}_{\mathbf{j}}=\{\begin{array}{ll}1& \text{ if }i=j\\ 0& \text{ otherwise }\end{array}$$
$$\Vert \mathbf{X}\widehat{{\mathbf{v}}_i}\Vert ={\sigma }_i$$
我们现在有了所有组成分解的部分。标量形式的奇异值分解只是第三个定义的重述。
$$\mathbf{X}{\hat{\mathbf{v}}}_{\mathbf{i}}={\sigma }_i{\hat{\mathbf{u}}}_i\text{\hspace{1em}(3)}$$
$\mathbf{X}$乘以一个特征向量${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$等于一个标量乘以另一个向量。
特征向量集合$\{{\hat{\mathbf{v}}}_1，{\hat{\mathbf{v}}}_2，\dots ，{\hat{\mathbf{v}}}_r\}$和向量集$\{{\hat{\mathbf{u}}}_1，{\hat{\mathbf{u}}}_2，\dots ，{\hat{\mathbf{u}}}_r\}$都是r维空间中的标准正交集或基。

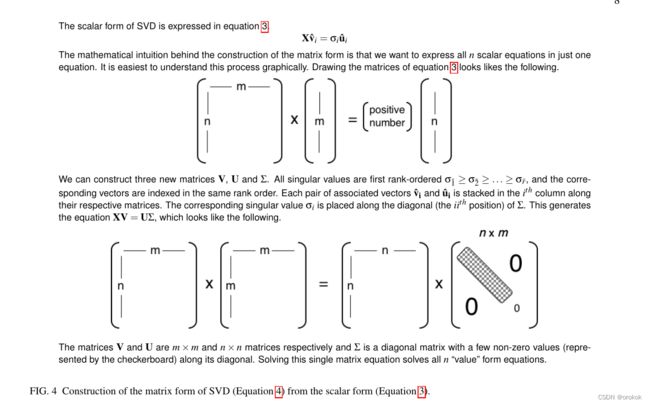
我们可以按照图4中规定的结构，在一次矩阵乘法中总结所有向量的结果。我们首先构造一个新的对角矩阵$\Sigma$。

其中${\sigma }_{\tilde{1}}\ge {\sigma }_{\tilde{2}}\ge \cdots \ge {\sigma }_{\tilde{r}}$是奇异值的秩有序集。同样地，我们构造伴随的正交矩阵，
$$\begin{gathered} \mathbf{V}=[{\hat{\mathbf{v}}}_{\tilde{1}}{\hat{\mathbf{v}}}_{\tilde{2}}\dots {\hat{\mathbf{v}}}_{\tilde{\mathbf{m}}}] \\ \mathbf{U}=[{\hat{\mathbf{u}}}_{\tilde{1}}{\hat{\mathbf{u}}}_{\tilde{2}}\dots {\hat{\mathbf{u}}}_{\tilde{\mathbf{m}}}] \end{gathered}$$
我们已经附加了一个额外的$(m-r)$和$(n-r)$标准正交向量来分别“填充”矩阵$\mathbf{V}$和$\mathbf{U}$
图4提供了一个图形表示，说明所有部分如何组合在一起形成SVD的矩阵版本。
$$\mathbf{XV}=\mathbf{U\Sigma }$$
其中$\mathbf{V}$和$\mathbf{U}$的每一列执行标量形式的分解(方程3)。
因为V是正交的，我们可以在两边同时乘以${\mathbf{V}}^{-1}={\mathbf{V}}^T$，从而得到分解的最终形式。
$$\mathbf{X}=\mathbf{U\Sigma }{\mathbf{V}}^{\mathbf{T}}\text{\hspace{1em}(4)}$$
虽然没有动机，但这种分解是相当强大的。方程4表明，任意矩阵X可以被转换为正交矩阵、对角矩阵和另一个正交矩阵(或旋转、拉伸和第二次旋转)。

6.2解读SVD

SVD的最后一种形式是简洁而厚重的陈述。让我们把方程3重新解释为
$$\mathbf{Xa}=k\mathbf{b}$$
其中$\mathbf{a}和\mathbf{b}$是列向量，k是标量常数。
集合$\{{\hat{\mathbf{v}}}_1，{\hat{\mathbf{v}}}_2，\dots ，{\hat{\mathbf{v}}}_m\}$类似于$\mathbf{a}$和集合$\{{\hat{\mathbf{u}}}_1，{\hat{\mathbf{u}}}_2，\dots ，{\hat{\mathbf{u}}}_n\}$类似于$\mathbf{b}$。
唯一的是$\{{\hat{\mathbf{v}}}_1，{\hat{\mathbf{v}}}_2，\dots ，{\hat{\mathbf{v}}}_m\}$和$\{{\hat{\mathbf{u}}}_1，{\hat{\mathbf{u}}}_2，\dots ，{\hat{\mathbf{u}}}_n\}$是向量的标准正交集合，它们分别张成m维和n维空间。

我们可以利用方程4使这个模糊的假设更加精确。
$$\begin{array}{rl}\mathbf{X}& =\mathbf{U}\Sigma {\mathbf{V}}^T\\ {\mathbf{U}}^T\mathbf{X}& =\Sigma {\mathbf{V}}^T\\ {\mathbf{U}}^T\mathbf{X}& =\mathbf{Z}\end{array}$$
我们已经定义了$\mathbf{Z}\equiv \Sigma {\mathbf{V}}^T$，注意前面的列$\{{\hat{\mathbf{u}}}_1，{\hat{\mathbf{u}}}_2，\dots ，{\hat{\mathbf{u}}}_n\}$现在是${\mathbf{U}}^T$中的行。
将此方程与方程1比较，$\{{\hat{\mathbf{u}}}_1，{\hat{\mathbf{u}}}_2，\dots ，{\hat{\mathbf{u}}}_n\}$的作用与$\{{\hat{\mathbf{p}}}_1，{\hat{\mathbf{p}}}_2，\dots ，{\hat{\mathbf{p}}}_m\}$相同。
因此，${\mathbf{U}}^T$是从$\mathbf{X}$到$\mathbf{Z}$的基底变换，就像之前一样，我们在变换列向量，我们可以再次推断我们在变换列向量。
事实上，标准正交基${\mathbf{U}}^T$(或$\mathbf{P}$)变换列向量意味着${\mathbf{U}}^T$是一个张成$\mathbf{X}$列的基。
跨列的基底被称为$\mathbf{X}$的列空间。列空间形式化了任何矩阵可能的“输出”的概念。
SVD有一个有趣的对称性，我们可以定义一个类似的量——行空间
$$\begin{array}{rl}\mathbf{VX}& =\Sigma \mathbf{U}\\ (\mathbf{XV}{)}^T& =(\Sigma \mathbf{U}{)}^T\\ {\mathbf{V}}^T{\mathbf{X}}^T& ={\mathbf{U}}^T\Sigma \\ {\mathbf{V}}^T{\mathbf{X}}^T& =\mathbf{Z}\end{array}$$
我们已经定义了$\mathbf{Z}\equiv {\mathbf{U}}^T\Sigma$，同样，${\mathbf{V}}^T$的行(或$\mathbf{V}$的列)是将${\mathbf{X}}^T$转换为$\mathbf{Z}$的标准正交基。因为$\mathbf{X}$的转置，$\mathbf{V}$是一个跨越$\mathbf{X}$的行空间的标准正交基。行空间同样形式化了什么是可能的“输入”到一个任意矩阵的概念。

6.3奇异值分解和主成分分析

可见PCA和SVD是密切相关的。让我们回到原始的$m\times n$数据矩阵$\mathbf{X}$，我们可以定义一个新的矩阵$\mathbf{Y}$为$n\times m$矩阵。
$$\mathbf{Y}\equiv \frac{1}{\sqrt{n}}{\mathbf{X}}^T$$
$\mathbf{Y}$的每一列均值都是0。通过分析${\mathbf{Y}}^{\mathbf{T}}\mathbf{Y}$, $\mathbf{Y}$的选择变得很清楚。
$$\begin{array}{rl}{\mathbf{Y}}^T\mathbf{Y}& ={\left(\frac{1}{\sqrt{n}}{\mathbf{X}}^T\right)}^T\left(\frac{1}{\sqrt{n}}{\mathbf{X}}^T\right)\\ & =\frac{1}{n}\mathbf{X}{\mathbf{X}}^T\\ {\mathbf{Y}}^T\mathbf{Y}& ={\mathbf{C}}_{\mathbf{X}}\end{array}$$
通过构造${\mathbf{Y}}^T\mathbf{Y}$等于$\mathbf{X}$的协方差矩阵。由第5节可知，$\mathbf{X}$的主成分是${\mathbf{C}}_{\mathbf{X}}$的特征向量。
如果我们计算$\mathbf{Y}$的SVD，矩阵$\mathbf{V}$的列包含${\mathbf{Y}}^T\mathbf{Y}={\mathbf{C}}_{\mathbf{X}}$的特征向量。
因此，$\mathbf{V}$的列是$\mathbf{X}$的主分量。
$\mathbf{V}$张成$\mathbf{Y}\equiv \frac{1}{\sqrt{n}}{\mathbf{X}}^T$的行空间。
因此，$\mathbf{V}$也必须张成列空间为$\frac{1}{\sqrt{n}}{\mathbf{X}}^T$。我们可以得出结论，找到主分量等于找到一个正交基它张成$\mathbf{X}$的列空间

七、讨论

主成分分析(PCA)利用线性代数的解析解揭示复杂数据集中简单的底层结构，因此具有广泛的应用前景。
图5提供了实现PCA的简要摘要。

在弹簧的例子中，PCA识别出大部分的变化存在于单个维度(运动方向$\hat{\mathbf{x}}$)，尽管记录了6个维度。
PCA是完全非参数的:任何数据集都可以插入，得到一个答案，不需要调整参数，也不考虑数据是如何记录的。
从一个角度来看，PCA是非参数化(即插即用)的事实可以被认为是一个积极的特征，因为答案是唯一的，独立于用户。
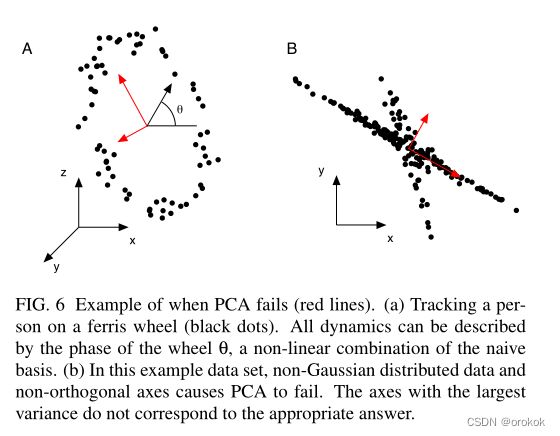
从另一个角度来看，PCA对数据的来源是不可知的这一事实也是一个弱点。例如，考虑在图6a中跟踪一个坐在摩天轮上的人。用车轮进动角$\theta$这一单一变量可以清晰地描述数据点，但主成分分析无法恢复这一变量。

7.1降维的极限与统计

更深层次的鉴赏PCA的限制需要考虑一些潜在的假设，在串联，更严格的描述的数据来源。一般来说，这种方法背后的主要动机是去关联数据集，即去除二阶依赖性。
PCA要求探索的每条新道路都必须与前一条道路垂直，但显然这一要求过于严格，数据(或城镇)可能会沿非正交轴线排列，如图6b。图6提供了这类数据的两个示例，其中PCA提供了不满意的结果。
在维数减少的情况下，衡量成功的一个标准是减少的表示在多大程度上可以预测原始数据。
在统计术语中，我们必须定义一个误差函数(或损失函数)。
可以证明，在一个共同的损失函数，均方误差(即L2范数)下，PCA提供了数据的最优简化表示。
这意味着选择主成分的正交方向是预测原始数据的最佳方案。
对于图6的示例，这种说法怎么可能是正确的呢?我们从图6中得到的直觉表明，这个结果在某种程度上是有误导性的。
这个悖论的解决方案就在于我们所选择的分析目标。分析的目标是去关联数据，或者换句话说，目标是消除数据中的二阶依赖关系。
在图6的数据集中，变量之间存在更高阶的依赖关系。因此，在揭示数据的所有结构时，去除二阶依赖关系是不够的。
存在多种消除高阶依赖关系的解决方案。
例如，在图6a中，可以检查数据的极坐标表示。这种参数化方法通常被称为核PCA。
另一个方向是对数据集中的依赖性进行更通用的统计定义，例如，要求减少维度的数据在统计上是独立的。这类算法，称为独立成分分析(ICA)，已被证明在许多领域成功的PCA失败。

附录A:线性代数

附录B:代码

---

Reference

A Tutorial on Principal Component Analysis