mne库脑电时频信号分析函数解读:小波变换及方法比较
2023/1/8-2023/1/9 脑机接口学习内容一览:
这一篇博客里,主要研究mne库中的函数mne.time_frequency.tfr_morlet如何完成时频信号分析,提供基本的函数功能、参数翻译以及部分参考用实践代码(包含完整注释)。本文内容较为基础,主要提供给脑机接口的初学者阅读。
mne.time_frequency.tfr_morlet
mne.time_frequency.tfr_morlet(inst, freqs, n_cycles, use_fft=False, return_itc=True,
decim=1, n_jobs=None, picks=None, zero_mean=True, average=True, output='power',
verbose=None)
使用小波计算信号的时频表示。
此函数计算与tfr_arrary_morlet相同,但是在epoch和evoke对象上操作,而不是在numpy数组上运行。
参数:
inst:传入epoch或evoke对象
freqs:数组或浮点数,感兴趣的频段
n_cycle:小波变换中的循环数,与freqs一起定义时间窗口长度
use_fft:是否基于fft的卷积
return_itc:返回试验一致性以及平均功效,若使用evoke数据则必须为false
decim:为了减少内存使用,时频分解后抽取系数
n_jobs:同时进行工作数量
picks:选取数据标准
zero_mean:是否确保小波的平均值为0
average:(不是很懂,这里摘取原文)
If False return an EpochsTFR containing separate TFRs for each epoch. If True return an AverageTFR containing the average of all TFRs across epochs.
output:默认为'power',若为'complex'则average为False
verbose:控制日志输出的详细程度
返回:
power:平均或单次功效
ITC:只有return_itc=True时生效
笔记:
(水平刚过六级,参考了部分资料作的翻译)
在基于时间的光谱分析中(与传统傅里叶方法一样),时间和光谱分辨率是相互关联的:时间窗口越长,则频率估计更精确;时间窗口较短,则频率估计越不精确,但反之提供更精确的时间定位信息。
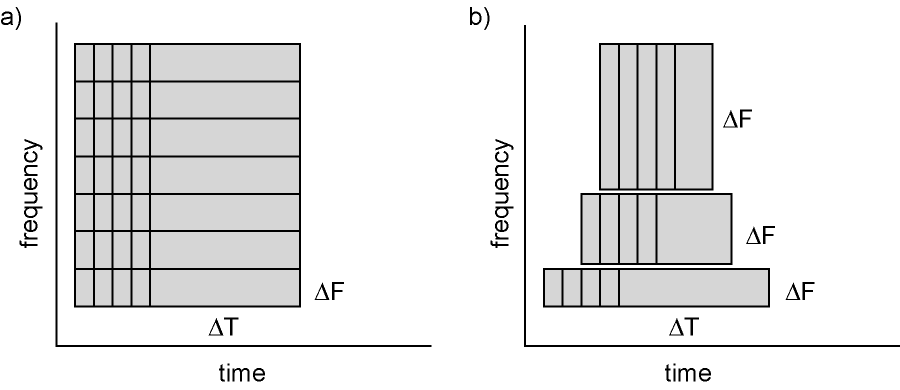
使用滑动时间窗口计算时频表示有两种不同的情况。时态窗口具有与频率无关的固定长度或长度随着频率的增加而减小。
(a) 对于时间窗口长度固定的情况,则时间和频率平滑保持固定。
(b) 对于时间窗口随频率而降低的情况,则时间平滑度降低,频率平滑度随频率增加。
在mne中,时间窗口的长度被freqs以及n_cycle所确定,在这两个参数确定之后,时间窗口长度 T = n_cycle / freqs。
例子:freqs=np.arange(1, 6, 2) 和 n_cycles=2 产生 T=array([2., 0.7, 0.4]).
这个n_cycle可能不太容易理解。我的理解是设定的频率把单位时间分为了确定数量的时间段,即 1 / freqs,根据不确定性原理,对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。而这个n_cycle就靠我们自己来根据频率估计确定。
根据查阅资料,小波变换继承和发展了短时傅里叶变换的局部化思想,同时又克服了窗口大小不随频率变化等缺点,能够提供一个随频率改变的“时间-频率”窗口。我原来以为窗口的大小是随着时间和频率自动调整的,可是从该函数出发看,窗口的大小似乎需要手动来确定。
mne.time_frequency.morlet
mne.time_frequency.morlet(sfreq, freqs, n_cycles=7.0, sigma=None, zero_mean=False)
计算给定频率范围之内的morlet小波。
与上一个函数似乎不太相同。前者通过小波变换来计算信号的时频表示,而后者计算的是信号使用的小波基的具体表示,即通过给定的参数生成小波。
参数:
sfreq:采样频率
freqs:用于计算小波的频率(可数组)
n_cycle:循环数,与前者参数相同,与freqs一起确定小波的宽度
sigma:它控制小波的宽度,即它的时间分辨率。如果 sigma 为“None”,则时间分辨率与所有小波变换一样与频率相适应。 频率越高,小波越短。 如果sigma是固定的,则时间分辨率是固定的,就像短时间傅里叶变换和震荡次数随着频率的增加而增加。
zero_mean:是否确保小波的平均值为0
返回:
Ws:小波时间序列
笔记:
在小波分析中,由n_cycles定义的振荡被一个高斯锥度逐渐变细,即小波的边缘被阻尼。这意味着报告周期数并不一定有助于理解已应用的时间平滑量。相反,可以报告小波半极大值处的全宽度(FWHM)。
不是很理解这一段。
应用函数程序实例:
(主要尝试使用tfr_morlet计算信号的频谱表示,参考文献【3】& main【4】)
数据的时频表示
(Multitaper vs. Morlet vs. Stockwell vs. Hilbert)
本例演示了模拟数据的不同时频估计方法。给出了时频分辨率权衡和估计方差问题。此外,它还强调了生成TFRs的替代函数,而无需在试验中求平均值,或通过操作numpy数组。
一开始我们先生成一段脑电模拟信号。
'''
使用已知的频谱时间结构来模拟数据
'''
# 设定采样频率
sfreq = 1000.0
# 设定频道名称
ch_names = ['SIM0001', 'SIM0002']
# 设定频道类型
ch_types = ['grad', 'grad']
# 根据以上信息创建info
info = create_info(ch_names=ch_names, sfreq=sfreq, ch_types=ch_types)
n_times = 1024 # 时间采样点数量,构造epoch的时间长度多于1秒1000
n_epochs = 40 # 构建epoch数量
seed = 42 # 设定种子
rng = np.random.RandomState(seed) # 根据种子生成随机数组,元素值在0-1之间
# 产生2行n_times*n_epochs+200列的标准正态分布随机数,长度为第二个参数所示
data = rng.randn(len(ch_names), n_times * n_epochs + 200)
# 添加一个50赫兹的正弦脉冲噪声和斜坡
# 返回0-1023的浮点数,除采样频率来表示时间采样点在以秒为单位的时间轴中的位置
t = np.arange(n_times, dtype=np.float64) / sfreq
# sin为数组中的每一个元素取正弦,t的系数为100pi,表示波的频率为100pi/2pi等于50hz
signal = np.sin(np.pi * 2. * 50. * t)
# 将信号中指定位置的t赋值为0,表示这些区域没有噪声,即只保留0.45s-0.55s的噪声信号
signal[np.logical_or(t < 0.45, t > 0.55)] = 0. # Hard windowing
print(signal.shape)
on_time = np.logical_and(t >= 0.45, t <= 0.55) # 设定取t范围
print(on_time)
# hanning生成长度为True数量的余弦窗口(即位于0.45s-0.55s的时间采样点个数),并乘在原数据区域上
signal[on_time] *= np.hanning(on_time.sum()) # Ramping
# 在data每一个频道的第一百个采样点到倒数第一百个采样点上加入噪声(持续1*20s)
print(data.shape)
data[:, 100:-100] += np.tile(signal, n_epochs) # add signal
raw = RawArray(data, info) # 建立raw结构
events = np.zeros((n_epochs, 3), dtype=int) # 建立一个shape为(20, 3)的0数组
events[:, 0] = np.arange(n_epochs) * n_times # 将第二个维度的第一个数值赋值为epoch所在的时间采样点位置
epochs = Epochs(raw, events, dict(sin50hz=0), tmin=0, tmax=n_times / sfreq,
reject=dict(grad=4000), baseline=None) # 建立epochs,将50hz波作为事件0输入
epochs.average().plot()计算信号的时频表示
下面我们选用这几个函数生成时频表示
多窗口变换
一开始我们使用多窗口变换来计算信号的时频表示。它在时频估计中创造了几个正交窗口用于减少方差。我们还将展示一些可以调整的参数(例如,time_bandwidth),这将导致不同的多锥属性,从而产生不同的TFR。你可以改变时间分辨率或频率分辨率,或两者兼有,以减少方差。
参数部分疑问见参考资料【5】相关部分以及前面小波变换函数的相似参数部分。
# 多窗口变换
# 生成感兴趣的频率数组
freqs = np.arange(5., 100., 3.)
print('freqs shape is ', freqs.shape)
vmin, vmax = -3., 3. # Define our color limits.
# 生成组合图,维度为(1, 3),详解可见之前博客或网上资料
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
for n_cycles, time_bandwidth, ax, title in zip(
[freqs / 2, freqs, freqs / 2], # 周期数 时间窗口长度 T=n_cycle/freqs,T过大时间精度不够,过小频率精度不够
[2.0, 4.0, 8.0], # 时间带宽积,越大计算次数越多,时间分辨率升高,频率分辨率降低,符合不确定性方程
axs,
['Sim: Least smoothing, most variance',
'Sim: Less frequency smoothing,\nmore time smoothing',
'Sim: Less time smoothing,\nmore frequency smoothing']):
power = tfr_multitaper(epochs, freqs=freqs, n_cycles=n_cycles,
time_bandwidth=time_bandwidth, return_itc=False)
ax.set_title(title)
# Plot results. Baseline correct based on first 100 ms.
power.plot([0], baseline=(0., 0.1), mode='mean', vmin=vmin, vmax=vmax,
axes=ax, show=False, colorbar=False)
plt.tight_layout()
plt.show()斯托克韦尔(S)变换
斯托克韦尔使用高斯窗口来平衡时间和光谱分辨率。重要的是,频段是相位归一化的,因此在时间方面严格可比较,并且如果我们忽略数值误差,输入信号可以无损地从变换中恢复。在这种情况下,我们通过使用width参数指定高斯窗口的不同宽度来控制光谱/时间分辨率。
具体见参考文献【6】,还是有点难理解。
# Stockwell (S) transform
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
fmin, fmax = freqs[[0, -1]]
for width, ax in zip((0.2, 0.7, 3.0), axs):
power = tfr_stockwell(epochs, fmin=fmin, fmax=fmax, width=width)
power.plot([0], baseline=(0., 0.1), mode='mean', axes=ax, show=False,
colorbar=False)
ax.set_title('Sim: Using S transform, width = {:0.1f}'.format(width))
plt.tight_layout()
plt.show()Morlet小波变换
接下来,我们使用morlet小波展示TFR,这是一个正弦波与高斯包络。我们可以使用n_cycles参数来控制光谱分辨率和时间分辨率之间的平衡,该参数定义了窗口中包含的周期数,大部分如前面函数解析所示。
# 小波变换
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
all_n_cycles = [1, 3, freqs / 2.]
for n_cycles, ax in zip(all_n_cycles, axs):
power = tfr_morlet(epochs, freqs=freqs,
n_cycles=n_cycles, return_itc=False)
power.plot([0], baseline=(0., 0.1), mode='mean', vmin=vmin, vmax=vmax,
axes=ax, show=False, colorbar=False)
n_cycles = 'scaled by freqs' if not isinstance(n_cycles, int) else n_cycles
ax.set_title(f'Sim: Using Morlet wavelet, n_cycles = {n_cycles}')
plt.tight_layout()
plt.show()窄带通滤波器与Hilbert变换
最后,我们将展示一个时频表示使用窄带通滤波器和Hilbert变换。选择正确的滤波器参数是很重要的,这样你就可以只分离出一个感兴趣的频段,通常这个滤波器的宽度建议约为2hz。
希尔伯特变换概念相关见参考文献【7】,说实话这个变换还是挺难理解的,顺便参考文献【8】复习一下卷积的概念。而简单来说,希尔伯特变换就是原始信号与1/pi t 做卷积,从频谱上来看,这个滤波器将我们的原始信号的正频率部分乘以-j,也就是说,保持幅度不变的条件下,将相位移动了-pi/2,而对于负频率成分,移动了pi/2。
# Narrow-bandpass Filter and Hilbert Transform
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
bandwidths = [1., 2., 4.] # 带通宽度
for bandwidth, ax in zip(bandwidths, axs):
data = np.zeros((len(ch_names), freqs.size, epochs.times.size),
dtype=complex)
for idx, freq in enumerate(freqs):
# 过滤原始数据并重新epoch以避免过滤器的时间过长
# 重新构造低频率和短周期的epoch数据
raw_filter = raw.copy()
# 注意:过滤器的带宽从默认值改变
# 夸大差异。使用默认的转换带宽,
# 这些都非常相似,因为过滤器几乎是一样的。
# 在实践中,使用默认值通常是明智的选择。
# 滤波器设置
raw_filter.filter(
l_freq=freq - bandwidth / 2, h_freq=freq + bandwidth / 2,
# 对于大带宽和低频率计算没有负值
# 过渡带宽度设定
l_trans_bandwidth=min([4 * bandwidth, freq - bandwidth]),
h_trans_bandwidth=4 * bandwidth)
# 该函数计算通道子集的分析信号或包络
raw_filter.apply_hilbert()
epochs_hilb = Epochs(raw_filter, events, tmin=0, tmax=n_times / sfreq,
baseline=(0, 0.1))
tfr_data = epochs_hilb.get_data()
tfr_data = tfr_data * tfr_data.conj() # compute power conj获取共轭复数
tfr_data = np.mean(tfr_data, axis=0) # average over epochs
data[:, idx] = tfr_data
power = AverageTFR(info, data, epochs.times, freqs, nave=n_epochs)
power.plot([0], baseline=(0., 0.1), mode='mean', vmin=-0.1, vmax=0.1,
axes=ax, show=False, colorbar=False)
n_cycles = 'scaled by freqs' if not isinstance(n_cycles, int) else n_cycles
ax.set_title('Sim: Using narrow bandpass filter Hilbert,\n'
f'bandwidth = {bandwidth}, '
f'transition bandwidth = {4 * bandwidth}')
plt.tight_layout()
plt.show()在不计算试验平均值的情况下计算TFR
也可以在不计算试验平均值的情况下计算TFR。我们可以使用average=False来做到这一点。在本例中,是mne.time_frequency的一个实例,返回EpochsTFR。
这样得到的图像与前面用小波变换的第三幅图像基本没有区别,因为之后power仍然使用了平均化,与前面相比基本只是多出了这一个步骤。
# Calculating a TFR without averaging over epochs
n_cycles = freqs / 2.
power = tfr_morlet(epochs, freqs=freqs,
n_cycles=n_cycles, return_itc=False, average=False)
print(type(power))
avgpower = power.average()
avgpower.plot([0], baseline=(0., 0.1), mode='mean', vmin=vmin, vmax=vmax,
title='Using Morlet wavelets and EpochsTFR', show=False)
plt.show()
全部代码:
import numpy as np
from matplotlib import pyplot as plt
from mne import create_info, Epochs
from mne.baseline import rescale
from mne.io import RawArray
from mne.time_frequency import (tfr_multitaper, tfr_stockwell, tfr_morlet,
tfr_array_morlet, AverageTFR)
from mne.viz import centers_to_edges
'''
Time-frequency on simulated data
(Multitaper vs. Morlet vs. Stockwell vs. Hilbert)
'''
'''
使用已知的频谱时间结构来模拟数据
'''
# 设定采样频率
sfreq = 1000.0
# 设定频道名称
ch_names = ['SIM0001', 'SIM0002']
# 设定频道类型
ch_types = ['grad', 'grad']
# 根据以上信息创建info
info = create_info(ch_names=ch_names, sfreq=sfreq, ch_types=ch_types)
n_times = 1024 # 时间采样点数量,构造epoch的时间长度多于1秒1000
n_epochs = 40 # 构建epoch数量
seed = 42 # 设定种子
rng = np.random.RandomState(seed) # 根据种子生成随机数组,元素值在0-1之间
# 产生2行n_times*n_epochs+200列的标准正态分布随机数,长度为第二个参数所示
data = rng.randn(len(ch_names), n_times * n_epochs + 200)
# 添加一个50赫兹的正弦脉冲噪声和斜坡
# 返回0-1023的浮点数,除采样频率来表示时间采样点在以秒为单位的时间轴中的位置
t = np.arange(n_times, dtype=np.float64) / sfreq
# sin为数组中的每一个元素取正弦,t的系数为100pi,表示波的频率为100pi/2pi等于50hz
signal = np.sin(np.pi * 2. * 50. * t)
# 将信号中指定位置的t赋值为0,表示这些区域没有噪声,即只保留0.45s-0.55s的噪声信号
signal[np.logical_or(t < 0.45, t > 0.55)] = 0. # Hard windowing
print(signal.shape)
on_time = np.logical_and(t >= 0.45, t <= 0.55) # 设定取t范围
print(on_time)
# hanning生成长度为True数量的余弦窗口(即位于0.45s-0.55s的时间采样点个数),并乘在原数据区域上
signal[on_time] *= np.hanning(on_time.sum()) # Ramping
# 在data每一个频道的第一百个采样点到倒数第一百个采样点上加入噪声(持续1*20s)
print(data.shape)
data[:, 100:-100] += np.tile(signal, n_epochs) # add signal
raw = RawArray(data, info) # 建立raw结构
events = np.zeros((n_epochs, 3), dtype=int) # 建立一个shape为(20, 3)的0数组
events[:, 0] = np.arange(n_epochs) * n_times # 将第二个维度的第一个数值赋值为epoch所在的时间采样点位置
epochs = Epochs(raw, events, dict(sin50hz=0), tmin=0, tmax=n_times / sfreq,
reject=dict(grad=4000), baseline=None) # 建立epochs,将50hz波作为事件0输入
epochs.average().plot()
'''
计算时频表示
'''
# 多窗口变换
# 生成感兴趣的频率数组
freqs = np.arange(5., 100., 3.)
print('freqs shape is ', freqs.shape)
vmin, vmax = -3., 3. # Define our color limits.
# 生成组合图,维度为(1, 3),详解可见之前博客或网上资料
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
for n_cycles, time_bandwidth, ax, title in zip(
[freqs / 2, freqs, freqs / 2], # 周期数 时间窗口长度 T=n_cycle/freqs,T过大时间精度不够,过小频率精度不够
[2.0, 4.0, 8.0], # 时间带宽积,越大计算次数越多,时间分辨率升高,频率分辨率降低,符合不确定性方程
axs,
['Sim: Least smoothing, most variance',
'Sim: Less frequency smoothing,\nmore time smoothing',
'Sim: Less time smoothing,\nmore frequency smoothing']):
power = tfr_multitaper(epochs, freqs=freqs, n_cycles=n_cycles,
time_bandwidth=time_bandwidth, return_itc=False)
ax.set_title(title)
# Plot results. Baseline correct based on first 100 ms.
power.plot([0], baseline=(0., 0.1), mode='mean', vmin=vmin, vmax=vmax,
axes=ax, show=False, colorbar=False)
plt.tight_layout()
plt.show()
'''
Stockwell (S) transform
'''
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
fmin, fmax = freqs[[0, -1]]
for width, ax in zip((0.2, 0.7, 3.0), axs):
power = tfr_stockwell(epochs, fmin=fmin, fmax=fmax, width=width)
power.plot([0], baseline=(0., 0.1), mode='mean', axes=ax, show=False,
colorbar=False)
ax.set_title('Sim: Using S transform, width = {:0.1f}'.format(width))
plt.tight_layout()
plt.show()
# 小波变换
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
all_n_cycles = [1, 3, freqs / 2.]
for n_cycles, ax in zip(all_n_cycles, axs):
power = tfr_morlet(epochs, freqs=freqs,
n_cycles=n_cycles, return_itc=False)
power.plot([0], baseline=(0., 0.1), mode='mean', vmin=vmin, vmax=vmax,
axes=ax, show=False, colorbar=False)
# 若n_cycle不为int,则赋值为字符串
n_cycles = 'scaled by freqs' if not isinstance(n_cycles, int) else n_cycles
ax.set_title(f'Sim: Using Morlet wavelet, n_cycles = {n_cycles}')
plt.tight_layout()
plt.show()
# Narrow-bandpass Filter and Hilbert Transform
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True)
bandwidths = [1., 2., 4.] # 带通宽度
for bandwidth, ax in zip(bandwidths, axs):
data = np.zeros((len(ch_names), freqs.size, epochs.times.size),
dtype=complex)
for idx, freq in enumerate(freqs):
# 过滤原始数据并重新epoch以避免过滤器的时间过长
# 重新构造低频率和短周期的epoch数据
raw_filter = raw.copy()
# 注意:过滤器的带宽从默认值改变
# 夸大差异。使用默认的转换带宽,
# 这些都非常相似,因为过滤器几乎是一样的。
# 在实践中,使用默认值通常是明智的选择。
# 滤波器设置
raw_filter.filter(
l_freq=freq - bandwidth / 2, h_freq=freq + bandwidth / 2,
# 对于大带宽和低频率计算没有负值
# 过渡带宽度设定
l_trans_bandwidth=min([4 * bandwidth, freq - bandwidth]),
h_trans_bandwidth=4 * bandwidth)
# 该函数计算通道子集的分析信号或包络
raw_filter.apply_hilbert()
epochs_hilb = Epochs(raw_filter, events, tmin=0, tmax=n_times / sfreq,
baseline=(0, 0.1))
tfr_data = epochs_hilb.get_data()
tfr_data = tfr_data * tfr_data.conj() # compute power conj获取共轭复数
tfr_data = np.mean(tfr_data, axis=0) # average over epochs
data[:, idx] = tfr_data
power = AverageTFR(info, data, epochs.times, freqs, nave=n_epochs)
power.plot([0], baseline=(0., 0.1), mode='mean', vmin=-0.1, vmax=0.1,
axes=ax, show=False, colorbar=False)
n_cycles = 'scaled by freqs' if not isinstance(n_cycles, int) else n_cycles
ax.set_title('Sim: Using narrow bandpass filter Hilbert,\n'
f'bandwidth = {bandwidth}, '
f'transition bandwidth = {4 * bandwidth}')
plt.tight_layout()
plt.show()
# Calculating a TFR without averaging over epochs
n_cycles = freqs / 2.
power = tfr_morlet(epochs, freqs=freqs,
n_cycles=n_cycles, return_itc=False, average=False)
print(type(power))
avgpower = power.average()
avgpower.plot([0], baseline=(0., 0.1), mode='mean', vmin=vmin, vmax=vmax,
title='Using Morlet wavelets and EpochsTFR', show=False)
plt.show()
学习总结:
在这三天的学习中,对脑电信号的时频分析方面有了更深一点的理解,但是对原理性的东西仍然不是很清楚。复杂的公式往往让人第一眼看过去就想放弃,数学水平尚待提升。
希望接下来的学习能让自己有更大的进步。因为要参加服务外包和复习期末考试的内容,最近花在脑机接口上的时间可能会少一点。但是概率论里的一些知识以及大物中的不确定性原理公式,服务外包中的数学建模思想以及python操作等等,这些都与我现在学习的脑机接口知识有一定的联系。我发现很多领域相互之间其实都是有一定关系在的,对于现阶段的我们来说,可能没有完全无意义的学习。
参考文献:
【1】小波变换的理解
【2】小波变换(wavelet transform)的通俗解释
【3】用MNE包进行Python脑电数据处理
【4】Time-frequency on simulated data (Multitaper vs. Morlet vs. Stockwell vs. Hilbert)
【5】matlab 功率谱密度 汉宁窗_【转】功率谱密度相关方法的MATLAB实现
【6】S变换
【7】希尔伯特变换(Hilbert Transform)简介及其物理意义
【8】卷积的通俗解释