HGKT : Introducing Hierarchical Exercise Graph for Knowledge Tracing
HGKT : Introducing Hierarchical Exercise Graph for Knowledge Tracing
主要内容
- HGKT : Introducing Hierarchical Exercise Graph for Knowledge Tracing
-
- Abstract
- 1 Introduction
- 2 Problem definition
- 3 HGKT Framework
-
- 3.1 Framework Overview
- 3.2 Direct Support Graph Construction
-
- 3.2.1 Knowledge-based Method
- 3.2.2 Bert-Sim Method.
- 3.2.3 Exercise Transition Method.
- 3.2.4 Exercise Support Method.
- 3.3 Problem Schema Representation Learning
- 3.4 Sequence Modeling Process
-
- 3.4.1 Sequence Propagation.
- 3.4.2 Attention Mechanism
- 3.4.3 Model Learning.
- 3.5 Prediction Output of HGKT
-
- 3.5.1 K&S Diagnosis Matrix.
- 3.5.2 Interpretability of Problem Schema.
- 4 EXPERIMENTS
-
- 4.1 Experiment Setup
-
- 4.1.1 Dataset and Preprocessing.
- 4.1.2 Implementation Details.
- 4.1.3 Comparison Baselines.
- 4.1.4 Evaluation Setting.
- 4.2 Comparison
- 4.3 Analysis
-
- 4.3.1 Ablation Study.
- 4.3.2 Graph Structure Analysis.
- 4.3.3 Effectiveness of Attention.
- 5 CASE STUDY
- 6 RELATEDWORK
-
- 6.0.1 Graph Neural Networks.
- 7 CONCLUSION
Abstract
知识追踪(KT)旨在预测学习者的知识掌握情况,在计算机辅助教育系统中发挥着重要作用。近年来,许多深度学习模型被应用于解决知识追踪的任务,并显示出良好的效果。然而,局限性仍然存在。大多数现有的方法将练习记录简化为知识序列,这就无法发掘练习中存在的丰富信息。此外,现有的知识追踪的诊断结果也不够令人信服,因为它们忽略了练习之间的先验关系。为了解决上述问题,我们提出了一个叫做HGKT的分层图知识追踪模型,以探索练习之间的潜在分层关系。具体来说,我们引入了问题模式的概念来构建一个层次化的练习图,该图可以模拟练习的学习依赖关系。此外,我们采用两种关注机制来突出学习者的重要历史状态。在测试阶段,我们提出了一个K&S诊断矩阵,可以追踪知识和问题模式的掌握情况,这可以更容易地应用于不同的应用程序。广泛的实验显示了我们提出的模型的有效性和可解释性。
1 Introduction
知识追踪是计算机辅助教育系统的一项基本任务,它可以使学习和教学都受益[1, 2, 18]。一个典型的知识追踪过程如下:当一个问题被发布后,学习者阅读其文本并应用知识来解决它。在得到一堆学习者的互动项目后,相应的知识序列和练习的互动序列被提取出来,以训练一个可以预测学习者的隐藏知识状态的KT模型。然而,在传统的知识追踪工作流程中,有两个主要问题。(1) 习题表述损失问题:传统工作流程将习题记录简化为知识序列,忽略了习题中包含的难度和语义信息。换句话说,现有的方法在表示习题的过程中存在着信息损失。(2)诊断不足的问题:根据诊断结果提供具体的学习建议也很困难。具体来说,假设我们知道一个学习者的知识比较薄弱(比如,),很难决定哪个更适合他(例如。7或8在图1中),因为知识和练习之间的映射过于广泛[15, 40]。
在文献中,有许多关于知识追踪的努力。
现有的方法可以分为两个轨道:基于传统知识的轨道和基于练习的轨道。传统的基于知识的方法将学习者的练习序列转换为知识序列,而不考虑练习的文本信息。最流行的是贝叶斯知识追踪(BKT)[5],它通过隐马尔可夫模型更新学习者的知识状态。深度学习方法,如深度知识追踪(DKT)将学习过程建模为一个递归神经网络[26]。动态键值记忆网络(DKVMN)通过引入两个记忆矩阵,分别代表知识和学习者对每个知识的掌握程度,增强了循环神经网络的能力[38]。基于图的知识追踪(GKT)将知识追踪与图神经网络相结合[25]。它将学习者的隐藏知识状态编码为图节点的嵌入,并在知识图中更新状态。
这些模型已被证明是有效的,但仍有局限性。
大多数现有的方法都面临着练习表征损失的问题,因为它们没有考虑到练习的文本。
对于基于练习的跟踪,据我们所知,练习强化知识跟踪(EKT)是第一个将练习文本的特征纳入知识跟踪模型的方法[16]。然而,EKT通过将练习文本直接输入双向LSTM网络来提取文本特征[14],这没有考虑到练习的潜在层次图性质,并带来了来自文本嵌入的额外噪声。
我们对解决习题表示损失问题和诊断不足问题的见解取决于充分探索习题之间潜在的层次图关系的想法。纳入练习之间的层次关系不仅可以提高学习者成绩预测的准确性,还可以提高知识追踪的可解释性。图1清楚地说明了层次关系是如何影响知识诊断结果的,以及我们的方法与传统知识追踪方法相比的优势。由于研究人员已经证明了将先决条件关系利用到KT任务中的有效性[3],我们将练习之间的层次图关系分解为直接支持和间接支持关系。支持关系的直觉是,它们代表了不同类型的练习学习依赖关系,可以作为知识追踪任务的约束条件。此外, 为了学习更精细的习题表示, 避免单一的习题噪音, 受数学解词技术[11, 37]的启发, 我们引入了问题模式的概念, 以总结一组具有类似解决方案的类似习题. 只有当两个练习属于同一个问题模式时,它们之间的关系才是间接支持。值得一提的是,我们假设每个练习只有一个主要知识和一个问题模式。考虑到属于不同知识的习题可能有类似的解决方案,而具有相同知识的习题也可能因其难度不同而属于不同的问题模式,我们假设知识和问题模式之间的关系是多对多的(如图2(a)所示)。
上述分析显示了将事先练习支持关系引入KT任务的前景。然而,它也可能带来以下问题。首先,练习之间的直接支持关系可以用多种方式定义,但哪种方式最适合于KT任务仍是未知数。第二,问题模式和间接支持关系的定义需要从语义的角度理解练习。如何自动理解和表示这些信息仍然是一个挑战。第三,层次化的练习关系包含不同层次的练习特征,如何有机地结合这些不同层次的特征仍然值得探索。最后,在我们对层次关系的信息进行编码之后,我们也希望模型在当前的预测过程中能够一直借鉴过去的关键信息。如图1所示,在对7进行预测时,我们的模型需要轻松地回顾重要的历史信息,如学习者在2中的错误答案或2与7之间的关系。
为了应对上述挑战,我们提出了一个名为HGKT的层次图知识追踪框架,它统一了层次图神经网络和递归序列模型的优势,并注意提高知识追踪的性能。综上所述,本文的主要贡献有以下几点:
- 我们引入了层次化练习图的概念,它由练习之间的直接和间接支持关系组成,可以作为知识追踪任务的学习约束。我们还提出了几种数据驱动的方法来模拟直接支持关系,并介绍了一种对间接支持关系进行语义建模的方法。
- 我们提出了练习的问题模式的概念,并探索了一种叫做层次图神经网络的新方法来学习问题模式的精炼表示。这种方法可以帮助解决练习表征损失的问题。
- 我们提出了两种注意机制,可以突出学习者的重要状态,并充分利用在HEG中学到的信息。
- 为了使诊断结果详细而有说服力,我们提出了一个知识与模式(K&S)诊断矩阵,可以同时追踪知识和问题模式的掌握情况(如图2(b)所示),这也有助于解决诊断不足的问题。
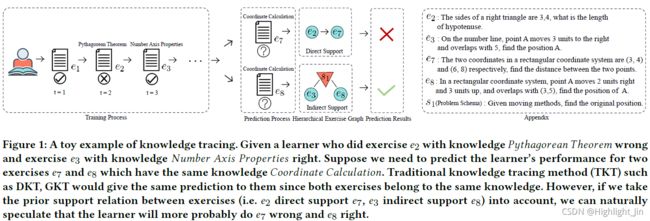
图1:知识追踪的一个玩具例子。给出一个学习者,他在做练习2时,知识 ℎ,做练习3时,知识 。假设我们需要预测学习者在两个练习中的表现7和8,这两个练习具有相同的知识 。传统的知识追踪方法(TKT),如DKT、GKT,会给他们同样的预测,因为这两个练习都属于同一个知识。然而,如果我们考虑到练习之间的先验支持关系(即2直接支持7,3间接支持8),我们自然可以推测,学习者更可能做错7而做对8。
2: 一个直角三角形的边是3,4,斜边的长度是多少。
3: 在数线上,点A向右移动3个单位并与5重叠,求A的位置。
7: 矩形坐标系中的两个坐标分别是(3,4)和(6,8),求这两点之间的距离。
8: 在矩形坐标系中,点A向右移动2个单位,向上移动3个单位,并与(3,5)重合,求A的位置。
s1: 给出移动的方法,求原来的位置。
2 Problem definition
我们在本文中对知识追踪的任务表述如下。知识追踪的目标是根据学习者的练习数据来估计学习者的隐藏知识状态。假设我们有一个学习者集P,一个练习集E,一个知识集K和一个问题模式集S。每个练习都与知识∈K和问题模式∈S相关联。我们进一步记录每个学习者l的练习序列为R={(1,1),(2,2)。. (, )},其中∈E,∈{0, 1}。这里 = 1表示一个正确的答案, = 0表示一个错误的答案。为了清楚地解释HGKT的框架,我们首先简要地介绍一下HEG的定义。
2.0.1 层次练习图(HEG)。在教育系统中,HEG是一个层次图,由不同层次的图组成,储存了练习之间的直接和间接支持关系。
具体来说,HGKT中使用的HEG有两个图:底部的图称为直接支持图,而顶部的图称为间接支持图。底部图的每个节点对应于我们数据库中的一个练习,而顶部图的每个节点对应于一个问题模式。底层图中的图链接是直接支持关系的模型,而这两个图之间的关系是间接支持关系的模型。形式上,我们将HEG图表示为(, , ),其中∈ {0, 1}|E |∗|E |是指 |E |∗|E |是底层图的邻接矩阵,∈R|E |∗是节点特征矩阵,假设每个节点有t个特征,∈R|E |∗|S|是分配矩阵,表示将底层图的每个节点分配到顶层图的某个节点。
3 HGKT Framework
3.1 Framework Overview
框架的整个结构如图3所示。在这里,系统1旨在通过层次图神经网络(HGNN)学习练习的层次图结构,并将这些资源提供给系统2。然后,系统2进行顺序处理,进行性能预测,并为系统1收集线索,以更好地完善每个问题模式的嵌入。为了开始训练,我们首先需要从练习数据库和交互历史中生成HEG。因此,我们在3.2节中介绍了几种构建直接支持图的方法,并在3.3节中从语义角度提取间接支持关系。
在构建HEG之后,练习记录和问题模式嵌入被结合到一个循环神经网络(RNN)中来预测学习者的表现。值得一提的是,HGNN和RNN是以端到端的方式进行训练的。
3.2 Direct Support Graph Construction
HGKT可以利用KT任务的练习之间的先验层次关系,如图1所示。然而,在大多数情况下,练习的层次关系是没有明确提供的。在这一节中,我们首先介绍几种方法来探索习题之间的直接支持关系,这些关系被进一步用于学习问题模式的表示。许多前辈已经证明了在KT任务中引入图结构的有效性[25, 33],因此我们在3.2.1, 3.2.2, 3.2.3节中提出了几种基于相似性规则的练习图结构。此外,基于贝叶斯统计推理,我们还提出了一种方法,可以利用训练集中练习互动序列的先验练习支持关系来构建直接支持图。为了将先验运动关系建模为约束条件,我们首先定义了以下关于运动支持关系的属性。属性1:我们用(1→2)来表示两个练习1和2的支持度。和表示学习者对给出正确或错误答案的事件。(1 → 2)的值越大,表明1和2的解有很强的支持度,这意味着如果我们知道一个学习者做错了1,那么他做错2的概率就越大。此外,如果已知学习者做对了2,那么他做对1的概率也很高。
( | ) > ( |, ), ( | ) > ( |, ), (1→2 ) > 0。
(1)属性2:反之,如果(1→2)很小,说明两个练习的内容和解决方案之间不存在先验支持关系。换句话说,学习者对这两个练习的表现 学习者的两个练习是两个不相关的事件。因此,我们可以进行以下公式的计算。 ( | ) = ( |, ), ( | ) = ( |, ), (1→2) = 0。
(2) 基于上述推理,我们构建练习之间的支持值如下。这里, ( ( , ) = ( , )计算在以答案回复之前以答案 的练习序列数量。此外,为了防止分母过小,我们在公式(3)和公式(4)中引入了拉普拉斯的平滑参数=0.01[9]。
(1 |2 ) = ( (2, 1) = (1, 1) ) + Í1 1=0 ( (2, 1) = (1, 1) ) + , (3) (1 |2, ) = Í1 =0 ( (2, 1) = ( , 1) + Í1 2=0 Í1 1=0 ( (2, 1) = ( 2, 1) + 。
(4) 同样地,我们也可以估计 (2 | )和 (2 |1, ) 的可能性。支持率的值被定义为以下两个部分的总和。这里,函数被用来确保支持率值的非负性。
(1 →2) = (0, ln ( | ) ( |,2 ) + (0, ln (2 | ) (2 |1, )。(5)
3.2.1 Knowledge-based Method
生成一个密集连接图,其中, 为1,如果两个不同的练习和包含相同的知识;否则为0。
3.2.2 Bert-Sim Method.
通过两个练习的BERT嵌入的余弦相似度生成一个图。这里, 是1,如果两个不同练习之间的相似度大于超参数;否则,是0。
3.2.3 Exercise Transition Method.
生成一个图,其邻接矩阵是一个过渡概率矩阵,其中,如果, Í|E| =1 , > ,则, 为 1;否则,为 0。这里, 代表练习j在练习i被回答后立即被回答的次数。
3.2.4 Exercise Support Method.
通过贝叶斯统计推理生成一个图,其中, 为1,如果( , ) > ;否则,为0。
3.3 Problem Schema Representation Learning
在这一节中,我们首先描述了探索练习之间间接支持关系的方法。所提取的层次关系被用来组成HEG。系统1的目标是为每个练习学习问题模式的表征,因此我们也提出了一种融合这些层次关系的方法。
挖掘间接支持关系的实质是为每个练习找到相应的问题模式(如图1所示),这可以转化为一个无监督的练习聚类问题。考虑到问题模式的语义性,我们使用BERT[6]对数据库中的所有习题进行编码,以获得其语义表示,因为许多成功案例已经证明了BERT理解文本背后的语义信息的能力。
此外,为了更好地获得多层次的聚类结果,以适应不同层次学生的认知特点,我们采用分层聚类[17]对BERT嵌入的练习进行聚类。层次聚类是一种无监督的聚类分析方法,使用聚类或分化策略来建立聚类的层次。我们可以设置不同的聚类阈值,得到不同层次的聚类结果,这可以用来寻找最适合问题模式的层次。此外,为了更好地结合图结构和练习的聚类结果,受DiffPool[36]中提出的赋值矩阵的启发,我们提出了一个练习赋值矩阵,可以提供直接支持图中每个练习节点对间接支持图中问题模式节点的赋值。这里,的每一行对应于底部图中的一个练习,而的每一列对应于顶部图中的一个问题模式。值得一提的是,DiffPool中的分配矩阵是由一个单独的GNN模型学习的,该模型的计算成本很高,而且在我们的案例中很难控制层次化的关系。
因此,我们使用分层聚类来生成分配矩阵以存储间接支持关系。
从练习中提取层次关系后,我们现在介绍在HEG中融合图信息的详细策略。在这里,我们提出了一个层次图神经网络(HGNN),将练习的语义特征传播到HEG的问题模式嵌入中(如图4所示)。HGNN由卷积层和池化层组成[20, 22, 28]。HGNN的关键直觉是,我们将带有练习信息的直接支持图和带有问题模式信息的间接支持图堆叠起来,并利用分配矩阵将每个节点从直接支持图分配到间接支持图。形式上,对于一个给定的HEG=(, , ),HGNN使用以下公式传播特征。首先,我们建立两个GNN网络,命名为和ℎ,其参数用于相应地更新练习嵌入和问题模式嵌入。
前k层的节点特征矩阵是每个练习和直接支持图的一热嵌入。这里和对应于练习和问题模式的嵌入。
请注意,0 = 。在第k层,如公式7所示,我们利用一个池操作来粗化直接支持图,以得到更小的间接支持图。在公式8中引入的线性变换将练习表示聚合为对应的问题模式表示。最后,ℎ更新问题模式的每个嵌入,并将此信息发送到HGKT的序列处理阶段。
H e ( l + 1 ) = G N N e x e r ( A e , H e ( l ) ) , l < k , \begin{aligned} H_{e}^{(l+1)} = GNN_{exer}(A_{e},H_{e}^{(l)}), l
3.4 Sequence Modeling Process
本节主要关注将问题模式的表示与序列信息相结合。
3.4.1 Sequence Propagation.
序列处理部分的总体输入是练习互动序列。每个练习互动包含三个部分:知识,练习结果,问题模式。这里,是对|K|不同知识的一热嵌入。是一个二进制值,表示学习者是否正确回答了一个练习。是HEG中生成的问题模式的嵌入。在每个时间步骤t,为了区分练习对其相应知识隐含状态的贡献,序列模型的输入是( , , ) 的联合嵌入。在传播阶段,我们使用RNN网络处理+1和之前的隐藏状态ℎ,得到当前学习者的隐藏状态ℎ+1,如公式10所示。这里我们使用LSTM作为RNN的一个变体, 因为它能更好地保留练习序列中的长期依赖性[14]. 公式11显示了对每个问题模式 +1∈R|S|在时间t+1的掌握情况的预测. {1, 1}是参数。
h t + 1 , c t + 1 = L S T M ( x t + 1 , h t , c t ; θ t + 1 ) , \begin{aligned} h_{t+1},c_{t+1} = LSTM(x_{t+1},h_{t},c_{t};\theta_{t+1}), \end{aligned} ht+1,ct+1=LSTM(xt+1,ht,ct;θt+1), m t + 1 c u r = R e L U ( W 1 ⋅ h t + 1 + b 1 ) . \begin{aligned} m_{t+1}^{cur}= ReLU(W_{1} \cdot h_{t+1}+b_{1}). \end{aligned} mt+1cur=ReLU(W1⋅ht+1+b1).
3.4.2 Attention Mechanism
HGKT利用两种注意机制,即序列注意和模式注意,来加强建模历史中典型状态的效果。
学习者在具有相同问题模式的练习中可能会有类似的表现,因此我们使用公式12中所示的序列注意来参考以前类似练习的结果。这里,我们假设历史问题模式掌握ᵅ +1的注意力是以前掌握状态的加权和汇总。然而,与[16]中使用的注意力不同,我们在HGKT中设置了一个注意力窗口限制,原因有以下两个。(1) 如果不限制序列注意力的长度,当练习序列非常长时,计算成本会很高。(2) 实验证明,最近的记忆比过去的长期记忆对知识追踪结果的影响更大,这与教育心理学是一致的,因为学习者会随着时间的推移开始失去对所学知识的记忆[7]。
m t + 1 a t t = ∑ i = m a x ( t − λ β , 0 ) t β i m i c u r , β i = cos ( s t + 1 , s i ) . \begin{aligned} m_{t+1}^{att}= \sum_{i=max(t-\lambda_{\beta},0)}^{t}\beta_{i}m_{i}^{cur}, \beta_{i}=\cos(s_{t+1},s_{i}). \end{aligned} mt+1att=i=max(t−λβ,0)∑tβimicur,βi=cos(st+1,si). 模式关注的目的是将学习者的注意力集中在一个给定的问题模式上,该模式具有∈R|S|,是与其他问题模式的相似性。如公式13所示,我们提出了一个外部存储器∈R∗|S|从间接支持图的最后一层的嵌入中收集。的每一列都对应于问题模式的一个嵌入。这里,k是HEG中的嵌入维度。公式13的直觉是,一个练习的答案将与具有类似问题模式的练习有关,因此我们可以将注意力集中在某个问题模式上。请注意,在训练过程中,记忆值随时间变化。
m t + 1 f = α t + 1 T m t + 1 c u r , α t + 1 = S o f t m a x ( s t + 1 T M s c ) . \begin{aligned} m_{t+1}^{f} = \alpha_{t+1}^{T}m_{t+1}^{cur}, \alpha_{t+1}=Softmax(s_{t+1}^TM_{sc}). \end{aligned} mt+1f=αt+1Tmt+1cur,αt+1=Softmax(st+1TMsc). 综上所述,预测学习者在时间t+1的表现的状态由三部分组成:当前知识掌握情况 +1,历史相关知识掌握情况 +1和焦点问题模式掌握情况 +1。如公式14所示,这些状态被串联起来,以预测最终结果。{2, 2}是参数。
r t + 1 ~ = σ ( W 2 ⋅ [ m t + 1 a t t , m t + 1 c u r , m t + 1 f ] + b 2 ) . \begin{aligned} \widetilde{r_{t+1}}= \sigma(W_{2} \cdot [m_{t+1}^{att},m_{t+1}^{cur},m_{t+1}^{f}]+b_{2}). \end{aligned} rt+1 =σ(W2⋅[mt+1att,mt+1cur,mt+1f]+b2).
3.4.3 Model Learning.
训练的目标是学习者反应的观察序列的负对数似然。在训练期间,两个参数,即ℎ,序列传播{1, 1,2, 2}中的参数被更新。
学习者的损失如公式15所示。具体来说,响应日志的损失被定义为时间t的真实答案和练习中预测的分数e之间的交叉熵。目标函数采用亚当优化法[19]进行最小化.
更多的实施细节将在实验部分介绍。
l o s s = − ∑ t ( r t l o g r t ~ + ( 1 − r t ) l o g ( 1 − r t ~ ) ) . \begin{aligned} loss = -\sum_{t}(r_{t}log\widetilde{r_{t}}+(1-r_{t})log(1-\widetilde{r_{t}})). \end{aligned} loss=−t∑(rtlogrt +(1−rt)log(1−rt )).
3.5 Prediction Output of HGKT
在对每个学习者从第1步到第t步的练习过程进行建模后,我们现在介绍了预测他在下一次练习+1中的表现的策略。此外,为了详细诊断学习者的学习过程,我们引入了一个K&S诊断矩阵,以动态地全面追踪知识和问题模式的掌握情况。
3.5.1 K&S Diagnosis Matrix.
与传统的知识追踪方法不同,HGKT在测试阶段的输入是练习的知识和问题模式。因此,我们可以在HGKT中追踪知识、问题模式或其组合的过渡掌握情况。具体来说,在每个时间步骤t,我们可以预测每个组合( , )( ∈K, ∈S)的表现。
因此,我们可以用这些结果生成一个矩阵 称为K&S诊断矩阵,其纵轴代表不同知识,横轴代表不同问题模式。接下来,如公式 17 所示,时间 t 的知识掌握程度 由每个问题模式的掌握程度加权汇总计算。
这里, 表示包含知识和问题模式的练习的数量。同样,我们可以计算出每个问题模式的掌握情况。
q i , j = ∣ { ( e ( k i , s j ) ∣ k i ∈ K , s j ∈ S ) } ∣ \begin{aligned} q_{i,j} = \left|{\{(e_{(k_{i},s_{j})}\mid k_{i}\in \mathcal K,s_{j}\in \mathcal S)}\}\right| \end{aligned} qi,j=∣∣{(e(ki,sj)∣ki∈K,sj∈S)}∣∣ R t , i k = R t , i k s d i k , d i , j k = q i , j ∑ j q i , j \begin{aligned} R_{t,i}^k = R_{t,i}^{ks}d_{i}^{k},\ d_{i,j}^{k} = \frac{q_{i,j}}{\sum_{j}q_{i,j}} \end{aligned} Rt,ik=Rt,iksdik, di,jk=∑jqi,jqi,j R t , j s = R t , j k s d j s , d i , j s = q i , j ∑ i q i , j . \begin{aligned} R_{t,j}^s = R_{t,j}^{ks}d_{j}^{s},\ d_{i,j}^{s} = \frac{q_{i,j}}{\sum_{i}q_{i,j}}. \end{aligned} Rt,js=Rt,jksdjs, di,js=∑iqi,jqi,j.
3.5.2 Interpretability of Problem Schema.
问题模式的引入可以有效提高模型对学习者成绩的预测效果。然而,问题模式的可解释性是未知的。基于上述挑战,我们提出了一种无监督的模式总结算法。该算法的核心思想是利用TextRank[24]来提取有意义的条件描述和相应的目标描述,并利用它们来形成基于某些规则的练习集群的描述。表1显示了一个对一组练习进行总结的例子。关于该算法的更多细节将在附录中介绍。
4 EXPERIMENTS
4.1 Experiment Setup
4.1.1 Dataset and Preprocessing.
由于没有公开的数据集可以提供带有文本信息的练习记录,我们的实验数据集来自一个大型的真实世界的在线教育系统。爱学堂在线系统1可以跟踪学习者的练习记录。每个学习者的记录包括学习者ID、讲座ID、课程类型、问题信息、回答时间、学习者的答案和纠正结果。问题信息包括问题ID、问题内容、问题类型和问题中包含的主要知识。为避免数据分布差异,我们使用2018年之后获得的数据。在数据预处理阶段,我们用学习者id对练习记录进行分组,并根据响应时间对记录进行排序。总的来说,我们从132,179名学习者那里得到91,449,914条回答记录。数据集的详细统计数据见表2。
4.1.2 Implementation Details.
为了建立HGKT的训练,我们首先需要使用无监督的数据来生成HEG。我们利用训练集中的练习互动数据来构建直接支持图,利用实验中涉及的所有练习数据来构建间接支持关系。因为前者的构建需要学习者的练习结果,而后者则只需要练习信息。
具体来说,我们利用公共的BERT-Base工具2,在没有任何微调的情况下,将每个练习转换为768维的嵌入向量,并在间接支持关系构建过程中利用分层聚类工具3。HGKT的框架是在构建HEG后进行联合训练。在测试阶段,我们使用相同的HEG来进行预测。
我们进行了大量的实验来寻找HGKT的最佳参数。在构建HEG的过程中,我们使用行使支持方法构建直接支持图,并将聚类阈值设置为9,然后得到1136个问题模式来构建间接支持图。在HGNN中,我们在的三个图卷积层和ℎ 的一个图卷积层得到了最佳结果。HGNN中的练习嵌入大小被设置为64,模式嵌入被设置为30。在序列传播阶段,我们将注意力窗口大小设置为20,LSTM隐藏嵌入大小为200。在训练过程中,我们使用学习率为0.01的Adam优化器,并将迷你批次设置为32。
我们还使用概率为0.5的dropout[30]来防止过拟合。
4.1.3 Comparison Baselines.
为了证明我们框架的有效性,我们将HGKT与以下先进的方法进行比较。这些方法从三个方面选择。(1) 传统的教育模型。贝叶斯知识追踪(BKT) (2)深度学习模型。深度知识追踪(DKT),动态键值记忆网络(DKVMN),练习感知知识追踪(EKT),图知识追踪(GKT)(3)HGKT的变体:HGKT-B,HGKT-S - BKT是一个传统的知识追踪模型,它是基于隐马尔科夫模型。每个概念的知识状态是一组二元变量[5]。
- DKT使用一个递归神经网络来模拟学习者的练习过程[26]。它将问题序列建模为知识序列。我们遵循[26]中提到的超参数,其中隐藏层的大小为200,我们对RNN使用一个GRU。
- DKVMN是一种深度学习方法,使用一个密钥矩阵来存储知识表示,并为每个学习者提供一个值矩阵来更新每个概念的掌握情况[38]。在实验中,当我们设定内存槽的大小为30,关键矩阵的嵌入大小为50,价值矩阵的嵌入大小为200时,我们得到了最好的结果。
- GKT是一种基于GNN的知识追踪方法,它将知识追踪任务重新表述为GNN中的时间序列节点级分类问题[25]。在实验中,我们使用过渡图法生成的知识图得到了最好的结果。
- EKT使用双向LSTM对练习文本进行编码,并利用注意力机制来提高预测的准确性[16]。在实验中,当其隐藏状态的形状为672和30时,我们得到最好的结果。
- HGKT-B是HGKT框架的一个变种。在这里,在建模过程中,我们不使用由HEG生成的问题模式嵌入。相反,我们使用BERT来编码文本特征。
- HGKT-S是HGKT框架的另一个变体。在建模过程中,我们使用由层次聚类产生的问题模式的单热来代替由HEG产生的问题模式的嵌入。
4.1.4 Evaluation Setting.
我们首先比较了HGKT与基线模型的整体性能。在实验中,我们随机选择60%,70%,80%,90%的练习记录作为训练数据,其余的作为测试数据。为了限定模型的有效性,我们从回归和分类两个角度比较实验结果[10, 21, 34]。我们使用开放源码平台来实现大多数比较基线模型,并搜索超参数以找到每个模型的最佳性能。我们的HGKT框架是由Torch在一台有8个英特尔至强Skylake 6133(2.5 GHz)CPU和4个Tesla V100 GPU的Linux服务器上实现的。对于所有模型,我们分别测试不同的参数和实验五次,最后取指标的平均值作为评价指标。
4.2 Comparison
图5显示了该任务的整体比较结果。结果表明,HGKT比其他基线模型表现得更好。
此外,我们从结果中得出了几个结论。(1) 我们提出的所有基于HGKT的模型都比其他基线模型表现更好。这一结果清楚地表明,HGKT框架可以充分利用运动记录和运动文本中包含的信息,有利于预测性能的提高。(2) HGKT-B的结果优于EKTA,这表明BERT比Bi-LSTM神经网络能更好地提取文本的表征。(3) HGKT-S比HGKT-B有更好的表现,这证明与直接使用每个练习的文本嵌入相比,用问题模式总结一堆类似的练习会带来更少的噪音。(4)HGKT的表现比HGKT-S好,这揭示了引入HEG进行问题模式表示学习也是有效的。原因可能是在HEG中,每个练习的表示是通过HGNN传播的,所以问题模式嵌入可以聚合某类练习的信息。
4.3 Analysis
为了了解HGKT中各种成分和超参数的影响,我们对Aixuexi数据集进行消融研究和参数分析。
4.3.1 Ablation Study.
我们研究了我们模型中不同支持关系和注意机制的影响。消减研究的结果显示在表4中。为了进行公平的比较实验,我们提出了具有相同框架但具有HGKT不同组件的方法。表4中的第一个方法采用了与HGKT相同的框架,但没有问题模式嵌入学习部分。第二种方法不包含练习的分层信息,只利用HEG的底层来学习每个练习的嵌入。
第三种方法只使用间接支持关系的信息,也就是密集层的层次聚类结果的单热,来学习每个问题模式的嵌入。
第四种方法放弃了层次图神经网络部分,直接合并了前两种方法学到的信息。上述所有方法都没有注意部分,这些学习到的嵌入被用来替代HGKT框架中的问题模式嵌入。与HGKT相比,第五种方法只缺少注意力部分。从结果来看,我们发现同时具有支持关系和注意力机制的HGKT表现得最好。我们还注意到,具有直接支持关系和间接支持关系的方法仍然优于没有这两种关系的实施。更有趣的是,我们还发现,直接合并两个支持关系比使用层次图神经网络的表现更差。我们推测,性能较差的一个可能的原因可能是由于单一练习引入的额外噪音。HGKT中的HGNN部分作为一个粗粒度的结构提取器,也是对一组类似练习的特征进行平均,从而减少了练习的噪音。
4.3.2 Graph Structure Analysis.
在HGKT中,有三个因素可能会影响分层练习图的结构:不同的直接支持图构建方法、问题模式聚类水平和HGNN中使用的层数。
在第3.2节中,我们提出了几种方法来探索练习的不同直接支持关系。这些方法决定了HEG中直接支持图的不同图结构。图6(a)显示了不同方法的知识追踪AUC。从图中,我们发现基于贝叶斯的图结构方法优于其他方法。一个潜在的原因可能是基于贝叶斯的方法可以利用运动交互历史中的信息,而不是像其他方法那样只使用运动特征。
我们还测试了不同边缘与节点比率对不同图形的影响(如图6(b)所示)。结果显示,当边缘与节点的比例约为3-4时,图卷积的效果最好。
问题模式的聚类水平会影响间接支持图中的节点数量。如图7(a)所示,当阈值为5时,问题模式的数量超过了3430个,这导致了密集的计算成本,而且生成的问题模式不够典型,无法代表一组练习。
因此,我们用5到20的阈值来测试HGKT的整体性能。图7(b)显示,当聚类阈值为9,问题模式的数量为1136时,出现了最佳的AUC。
此外,从曲线的整体趋势来看,我们可以推断出有一个最适合的习题划分,这意味着使用问题模式来代表一组相似的习题是合理的。
在和ℎ,所用的图卷积层的数量也是可调整的超参数。因此,我们研究了图卷积层的数量对我们模型性能的影响。表3显示了实验的结果。
我们发现,-3_-1版本在KT任务中取得了最好的结果。原因可能是-3_-1结构可以实现最佳的信息聚合能力。
4.3.3 Effectiveness of Attention.
正如我们在注意力机制部分所阐明的,带有注意力的HGKT可以增强网络的记忆能力。该模型可以观察以下信息来预测学习者在练习中的表现:过去类似练习的表现,学习者当前的知识状态,学习者当前的注意力。为了证实这两种注意力机制的有效性,我们设立了以下两个实验。首先,我们将HGKT与以下三种模型进行比较。HGKT-noa, HGKT-sche和HGKT-seq。
HGKT-noa是HGKT的一个无注意力版本。同样,HGKT-sche和HGKT-seq是HGKT的变种,分别只包含模式注意和序列注意。图8(a)显示了它们的比较结果。从图中,我们可以推断出HGKT优于其他比较方法。此外,HGKT-sche和HGKT-seq都比HGKT-noa表现更好,这证明这两种注意机制都可以为HGKT模型作出贡献。此外,我们还进行了实验来观察序列注意的不同窗口大小的影响。在实验中,我们将窗口大小的长度设置为10到50,以观察哪种大小可以更好地保存对KT有用的记忆。如图8(b)所示,窗口大小的最佳参数是20,这揭示了近20个练习的结果可以最好地反映他们当前的学习状态。这个值为设置学习者能力测试中的练习数量提供了一个很好的参考。
5 CASE STUDY
问题模式和HEG的引入可以使诊断更加准确,提高诊断结果的可解释性。
此外,由HGKT生成的诊断结果可以很容易地应用于以下两种应用。(1)学习者诊断报告[27, 32] (2)自适应问题推荐[4, 23]。
为了对上述说法进行深入分析,我们在图9中对学习者在练习过程中的知识掌握情况进行了可视化的预测。
从图中我们可以更直观地了解HGKT与传统知识追踪诊断(TKT)相比的优势。当=8时,学习者做错了12,TKT的诊断结果显示,与7相关的知识颜色(如29)变得更深。然而,对相关知识掌握得不好的原因仍然不明。在HGKT中,可以发现学习者掌握知识的转变与图9(b)中的局部HEG图密切相关。具体来说,学习者在12中的错误导致对知识7、23和29的掌握不佳,这表明纳入直接和间接支持图确实会影响诊断的结果。
此外,HEG信息也可以在某种程度上解释知识掌握的变化,所以学习者的诊断报告可以更加可靠。图中的QA部分通过比较HGKT和TKT对几个问题的解释,显示了HGKT的可解释性的提高。通过K&S诊断矩阵法,学习者不仅可以知道没有掌握某些知识的根本原因(如:1,1),还可以通过更有针对性和准确的训练建议来提高知识的掌握程度,这揭示了HGKT框架可以更好地应用于自适应问题推荐场景。
6 RELATEDWORK
6.0.1 Graph Neural Networks.
图神经网络(GNN)可以为图结构的数据建模,如社交网络数据[13, 20, 31]或知识图数据[8, 29, 39],最近引起了极大的关注。GNN通过转换、传播和聚集节点特征来学习节点表征,并被证明对大多数图结构数据有效[12, 13]。然而,目前的GNN架构的能力是有限的,因为它们的图是固有的平坦的,因为它们只在图的边缘传播信息,不能以分层的方式推断和聚合信息[28, 35]。DiffPool[36]是一种可微分的图池方法,它首先被提出来学习可解释的图的分层表示。然而,它需要训练一个单独的集群分配矩阵,计算成本很高。
因此,我们在论文中提出了DiffPool的一个变种,用于学习节点表示。
7 CONCLUSION
在这篇文章中,我们证明了练习之间的层次关系对于KT任务的重要性。为了充分利用习题中的文本信息,我们提出了一个新的知识追踪框架HGKT,它利用了层次化习题图和序列模型的优势,注意提高知识追踪的能力。此外,我们提出了K&S诊断矩阵的概念,可以追踪知识和问题模式的掌握情况,这在工业应用中已经被证明比传统的知识追踪方法更有效和有用。此外,我们构建了一个包含练习文本信息的大规模知识追踪数据集,并进行了广泛的实验,以显示我们所提出的模型的有效性和可解释性。