微积分——导数和切线问题

目录

1.  切线(Tangent Line)问题

2.  函数的导数(derivative)

3.  函数的可微性(differentiability)与连续性(Continuity)

---

1.  切线(Tangent Line)问题

微积分的出现源于17世纪欧洲数学家们正在研究解决的四个主要的问题：

(1) 切线(tangent line)问题；

(2) 速度(velocity)和加速度(acceleration)问题；

(3) 最小值(minimum)和最大值(maximum)问题；

(4) 面积(area)问题。

以上每一个问题都包括极限的概念，而且，微积分可以由以上任意一个问题引入。因此，下面从切线问题入手引入微积分。

尽管皮埃尔·德·费马(Pierre de Fermat)(法国，1601–1665)、笛卡尔(法国，René Descartes) (1596–1650)、克里斯蒂安·惠更斯(Christian Huygens)(荷兰，1629–1695) 和伊萨克·巴罗(英国，Isaac Barrow)(1630–1677)都给出了切线问题的部分解，但据信给出第一个通解的是艾萨克·牛顿(Isaac Newton)(英国，1642–1727) 和戈特弗里德·莱布尼茨(Gottfried Leibniz)(德国，1646–1716)。牛顿在这个问题上的工作源于他对光学(optics)和光折射(light refraction)的兴趣。(注：关于切线问题，在1637年，数学家笛卡尔指出：“And I dare say that this is not only the most useful and general problem in geometry that I know, but even that I ever desire to know.(我敢说，这不仅是我所知道的最有用、最普遍的几何问题，而且是我一直渴望知道的问题。)”)

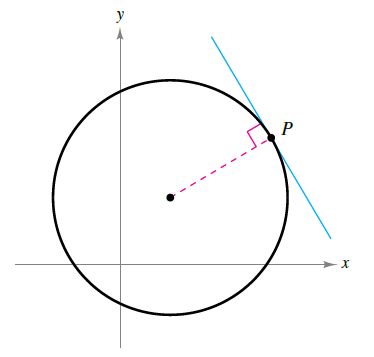
一条直线在曲线上的某一点与曲线相切是什么意思呢？对于一个圆，圆上某一点P的切线是在P点与径线(radial line)垂直(perpendicular)的直线,如图1.1所示。

 ----------------------------图1.1  图的切线---------------------

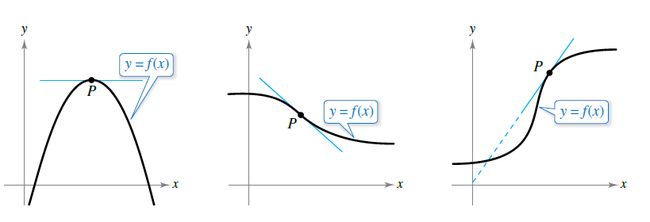
然而，对于任意曲线，问题更加复杂。例如，对于1.2中的曲线，你想如何定义曲线的切线呢？你可能会说，当一条直线与曲线上某一点P相接触时，它就与这条曲线相切。这种定义对于图1.2中的第一种曲线适用(它是对称的，点与曲线不相交)，但却不适用于第二种曲线(直线与曲线有效点)。或者，你可能会说，当一条直线与这条曲线在某一点恰好接触或者相交(intersects)时，这条直线便是为条曲线的一条切线。这种定义适用于圆，但却不适用于任意曲线，例如，图1.2中第三种曲线(既相切又相交)。

-------------------------图1.2 曲线上某一点的切线----------------

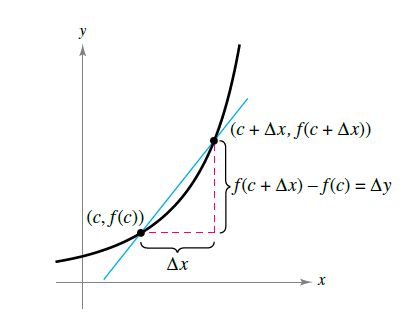
 在本质上，求曲线上某一点P的切线问题，归结为求得曲线上某一点P的切线的斜率(slope)问题。您可以使用穿过切点(the point of tangency)和曲线上第二个点的割线(secant line)来近似地表示此斜率，如下图1.3。

-------------图1.3  穿过点(c,f(c))和点(c+Δx,f(c+Δx))的切线----------------

 假如(c,f(c))是切点(the point of tangency)，并且

(c+Δx,f(c+Δx))

是函数f图像上的第二个点，则通过这两个点的割线的斜率可以通过代入斜率公式算出

    （y的变化/x的变化）

     (切线的斜率)

等式的右边是函数的差商(difference quotient)。分母(denominator) Δx是x轴方向的变化值，分子

Δy = f(c+Δx) – f(c)

是y轴方向的变化值。

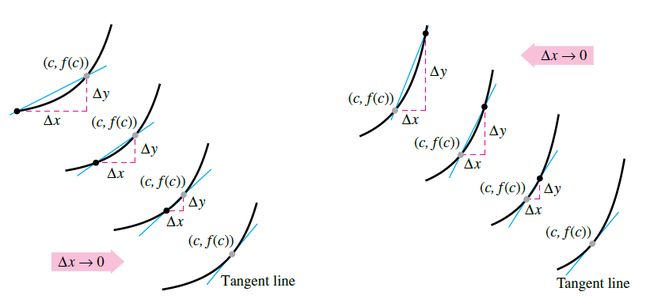
这个例程(procedure,即使用斜率公式表示法)的美妙之处在于，您可以通过选择越来越接近切点的点来获得越来越准确的切线斜率近似值，如下图1.4所示

-----------------------图1.4 切线近似值-----------------------------------

具有斜率m的切线的定义

假如f是定义在包含c点的开区间上的函数，并且假如以下极限

存在,则穿过点(c, f(c))且具有斜率m的直线就是函数f的图像上位于点(c, f(c))处的切线(tangent line)。

函数f 的图像上位于点(c, f(c))处的切线的斜率也称为函数f的图像上位于点x=c处的斜率。

2.  函数的导数(derivative)

用于定义切线斜率的极限也用于定义微积分的两个基本操作之一——微分(differentiation)。这是微积分的关键点。

函数导数的定义

假如f的极限存在，则函数f 位于x点的导数是

对于这种极限存在的所有x, 函数f的导数 f ’也是x的函数。

(注：关于导数(derivative)这个概念，由于函数的导数f ’是由函数f“导出的、衍生出的、演绎出的、推导出的、等等(derived)”,因此，中文将其译为“导数”。)

应该认识到，x的函数的导数也是x的函数，这个“新产生”的函数给出了对于任意点(x,f(x))的f函数图形上的切线斜率(slope)(假如函数图形在这一点处有切线)。这个导数也可以用于确定一个变量针对别一个变量的“变化的瞬时率”(或简称“变化率”)。

因此，从定义上可以看出，导数的确切数学含义为“当函数的变化率(即Δx无限接近0时)接近于零时，函数的变化值与其自变量的相应变化值之比的极限值”，简单说，就是函数导数是“变化率的极限值”(注：将“导数”说成是“微商”是不严谨的)。

求这个导数的过程称为微分(differentiation)。当一个函数在x点的导数存在，则这个函数在x点可微(differentiable),且当它在开区间(a,b)上的每一点都可微，则此函数在开区间(a,b)上可微。

导数除了记为f′(x)，最常用的记法还有

 (导数的概念)

记法dy/dx读作“y针对x的导数”，或简单读为“dy，dx”，使用极限记，您可以写作

3.  函数的可微性(differentiability)与连续性(Continuity)

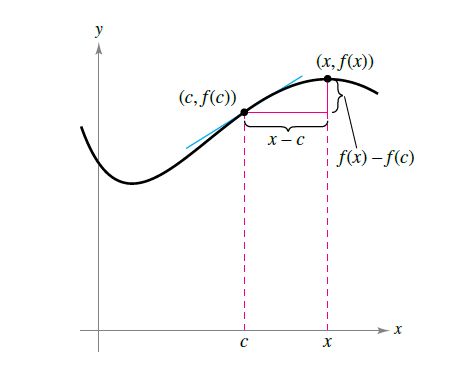
下面所示的函数导数的等价形式对于考察可微性与连续性之间的关系十分有用。如下图1.3假设极限存在，则函数f 位于c点的导数是

   (导数的等价形式)

------------图1.5  随着x趋近于c，割线趋近于切线----------------------

需要指出的是，这个等价形式的极限存在的要求是单侧极限

和

存在且相等。这两个单侧极限分别称为函数从左侧的导数(简称“左导数”)和函数从右侧的导数简称“右导数”。等价表示法遵循的法则是：当f在开区间(a,b)上可微且a的右导数和b的左导数都存在的时候，它在闭区间[a,b]上可微。

当一个函数在x=c点不连续时，它在x=c点也不可微。

定理：可微性意味着连续性。

即，假如函数f在x=c点可微，则f在x=c点连续。

连续性和可微性的关系总结如下：

(1) 假如一个函数在x=c点可微，则它在x=c点连续。因此，可微性意味着连续性。

(2) 假如一个函数在x=c点连续，但它在在x=c点不具可微性，这种情况是可能的。因此，连续性并不意味着可微性(例如，垂直切线函数在x=0处，突变函数|x-2|在x=2处)。

内容来源：

1. 网络资源

2. <> Ron Larson,The Pennsylvania State University The Behrend College
Bruce Edwards, University of Florida