GAMES101-现代计算机图形学-闫令琪 作业2 反走样 antialiasing 抗锯齿
文章目录
- 简介
- MSAA问题
-
- 1、黑边情况1
- 2、黑边情况2
- 3、灰边情况
- SSAA
- 总结
-
- MSAA
- SSAA
- 最后
- 参考
简介
本文章主要内容为作业二的最后一个题目:反走样的处理。本文使用了两种反走样的办法,ssaa和msaa。在实现的过程中遇到了几个问题与大坑,大家有同样类似问题的不妨看看。
tips:反走样结果图片均按照4x4频率来采样。
MSAA问题
1、黑边情况1
最开始实现的反走样在两个三角形的交界处会产生黑色的边,如下面所示。


其原因主要为:这时采用的为原图片大小的深度缓存空间,两个三角形位置为关系为绿色在上(前),蓝色在下(后)面,绘制时的顺序也按照这样。在计算完绿色三角形之后,帧缓存和深度缓存均已更新,三角形边缘的地方像素颜色采用覆盖比率插值计算,深度值为绿色三角形在该坐标所计算出的深度插值。根据上面的话,这条黑色的边其实并不是真的的黑色,而是插值之后的绿色,只不过是由于覆盖比率很小在插值之后rgb值变得很低,颜色的饱和度与亮度会随之下降。例如原rgb值为(200,200,100),若覆盖比率为4/16的话,如下面效果,若覆盖率更低那么会更接近黑色。


在计算完第一个绿色的三角形之后,开始计算第二个蓝色的三角形,这时又遍历到了上面异常的黑边处,也就是有一点点绿色的黑边,需要比较深度缓存来决定蓝色三角形是否要在该像素绘制。在每个像素采样计算时,三角形的覆盖是按照4x4采样计算的,但是深度值是按照像素级别1x1计算和存储来的, 之前该像素位置只存储了绿色三角形的深度值,蓝色三角形在绿色之后,所以深度比较失败,从而导致了该处不会再更新像素值。
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
int sampling_frequency, sampling_times;
sampling_frequency = 4;
sampling_times = sampling_frequency * sampling_frequency;
float sampling_period = 1.0f / sampling_frequency;
int minX = width, minY = height, maxX = 0, maxY = 0;
for (auto vert : v) {
if (vert.x() < minX)
minX = vert.x();
if (vert.y() < minY)
minY = vert.y();
if (vert.x() > maxX)
maxX = vert.x();
if (vert.y() > maxY)
maxY = vert.y();
}
Vector3f color = t.getColor();
for (int i = minY; i < maxY; i++) {
for (int j = minX; j < maxX; j++) {
float z_depth = 0,blend_rate;
int coloring_block_counter = 0;
for (int m = 0; m < sampling_frequency; m++) {
for (int n = 0; n < sampling_frequency; n++) {
float x = j + (n + 0.5f) * sampling_period;
float y = i + (m + 0.5f) * sampling_period;
if (insideTriangle(x, y, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
z_depth += z_interpolated;
coloring_block_counter++;
}
}
}
if (coloring_block_counter > 0) {
z_depth = z_depth / coloring_block_counter;
blend_rate = 1.0f * coloring_block_counter / sampling_times;
Vector3f point = { j * 1.0f,i * 1.0f,0.0f };
if (z_depth < depth_buf[get_index(j, i)]) {
depth_buf[get_index(j, i)] = z_depth;
Vector3f color = t.getColor() * blend_rate ;
set_pixel(point, color);
}
}
}
}
}
2、黑边情况2
如果只使用与图像大小同样的帧缓冲空间和深度缓冲空间,上述情况可能是无解的,也就是边缘处靠后绘制的图像若位置也在后面(深度差值比较失败)将无法更新像素值从而产生“黑边”,如果有请告诉我!
上述的情况是因为深度缓冲采样率不足所导致的,所以按照采样率扩大深度缓存空间。这个时候在计算深度缓存的时候一个像素是按照4x4频率来计算的,可以存储多个深度值并更新和计算各个三角形的边缘像素的覆盖比率。

如上图所示红框为1个像素,在内部做4x4的采样,其深度缓存如上所示。

开始计算第一个绿色三角形的在该像素的覆盖率,其中绿色块为该三角形在这个像素进行4x4采样时所覆盖的区域 (仅用来图示表示覆盖的区域,不做存储),满足覆盖的采样区域会计算深度插值,并比较和更新深度值。最后按照覆盖比率计算该像素的rgb插值并存储。

在计算第二个蓝色三角形时又到了这个像素,在该像素内计算蓝色三角形的深度插值并更新存储,最后根据覆盖比率计算这个像素的rgb插值。
#define Freq 4 //采样频率
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h) {
frame_buf.resize(w * h);
depth_buf.resize(w * h*Freq*Freq);
}
int rst::rasterizer::get_depth_buf_index(int x,int y) {
return (height*Freq-1-y)*width*Freq+x;
}
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
int sampling_frequency, sampling_times;
sampling_frequency = Freq;
sampling_times = sampling_frequency * sampling_frequency;
float sampling_period = 1.0f / sampling_frequency;
int minX = width, minY = height, maxX = 0, maxY = 0;
for (auto vert : v) {
if (vert.x() < minX)
minX = vert.x();
if (vert.y() < minY)
minY = vert.y();
if (vert.x() > maxX)
maxX = vert.x();
if (vert.y() > maxY)
maxY = vert.y();
}
Vector3f color = t.getColor();
for (int i = minY; i < maxY; i++) {
for (int j = minX; j < maxX; j++) {
float blend_rate;
int sample_counter = 0;
for (int m = 0; m < sampling_frequency; m++) {
for (int n = 0; n < sampling_frequency; n++) {
float x = j + (n + 0.5f) * sampling_period;
float y = i + (m + 0.5f) * sampling_period;
if (insideTriangle(x, y, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
int depth_buf_x, depth_buf_y;
depth_buf_x = j * Freq + n;
depth_buf_y = i * Freq + m;
if (z_interpolated < depth_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)]) {
depth_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)] = z_interpolated;
sample_counter++;
}
}
}
}
if (sample_counter > 0) {
blend_rate = 1.0f * sample_counter / sampling_times;
Vector3f point = { j * 1.0f,i * 1.0f,0.0f };
Vector3f color = t.getColor() * blend_rate ;
set_pixel(point, color);
}
}
}
}
这黑边怎么还在!但是仔细一看和原来的有些不同,之前的“黑边”在外侧,现在的“黑边”是在内侧,这同时也说明蓝色的三角形像素已经更新到帧缓存中了,只不过是深蓝的“黑边”。


这是因为只是单单把这个像素更新为深蓝色了,而之前的绿色直接被磨掉,所以可以采取下面的插值方法来混合之前所存储的rgb值。但是效果也不太理想,混合之后依然会有条灰色的线。
Vector3f color = t.getColor() * blend_rate + frame_buf[get_index(j, i)] * (1 - blend_rate);
3、灰边情况
为了解决这个问题,我采取了一个折中的办法。在像素中采样的时候记录两个状态:三角形覆盖计数和深度值更新计数。第一个为计算三角形在该像素的覆盖比率,第二个为计算该像素内深度值更新的比率。只有在该像素有更新深度值的情况下才会按照覆盖比率绘制该像素,否则无论无论覆盖多少都不会更新像素(防止图像深度出现问题)。不过这样做也有缺点,原来的“黑灰边”处会被后来的图像颜色所控制,如下图。


这里的蓝色三角形在这些“灰色”像素的覆盖率为16/16所以原来的插值颜色会直接丢失,这些地方的反走样效果也会消失。这种情况似乎无法避免,要么有“灰黑色”像素,要么就是“灰黑色”像素被完全替换。上述情况似乎是个互相对立的矛盾,二者只能取其一,还未想到更好的解决办法。
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
int sampling_frequency, sampling_times;
sampling_frequency = Freq;
sampling_times = sampling_frequency * sampling_frequency;
float sampling_period = 1.0f / sampling_frequency;
int minX = width, minY = height, maxX = 0, maxY = 0;
for (auto vert : v) {
if (vert.x() < minX)
minX = vert.x();
if (vert.y() < minY)
minY = vert.y();
if (vert.x() > maxX)
maxX = vert.x();
if (vert.y() > maxY)
maxY = vert.y();
}
Vector3f color = t.getColor();
for (int i = minY; i < maxY; i++) {
for (int j = minX; j < maxX; j++) {
float cover_rate;
int cover_sample_counter = 0, depth_update_counter=0;
for (int m = 0; m < sampling_frequency; m++) {
for (int n = 0; n < sampling_frequency; n++) {
float x = j + (n + 0.5f) * sampling_period;
float y = i + (m + 0.5f) * sampling_period;
if (insideTriangle(x, y, t.v)) {
cover_sample_counter++;
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
int depth_buf_x, depth_buf_y;
depth_buf_x = j * Freq + n;
depth_buf_y = i * Freq + m;
if (z_interpolated < depth_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)]) {
depth_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)] = z_interpolated;
depth_update_counter++;
}
}
}
}
if (depth_update_counter>0) {
cover_rate = 1.0f * cover_sample_counter / sampling_times;
Vector3f point = { j * 1.0f,i * 1.0f,0.0f };
Vector3f color = t.getColor() * cover_rate + frame_buf[get_index(j, i)] * (1 - cover_rate);
set_pixel(point, color);
}
}
}
}
SSAA
ssaa我所采用的方法比较简单,使用按采样率变化扩展的深度缓存、临时帧缓存,也就是在原来的width*height空间中根据采样率计算,再将计算结果全部映射到 width * 采样率 * height * 采样率 这个空间中去存储和查询。最后在临时帧缓冲空间中来降采样,将其降到原空间大小,查询、相加、求均值即可。
#define Freq 4
void rst::rasterizer::down_sampling() {
int sampling_frequency, sampling_times;
sampling_frequency = Freq;
sampling_times = sampling_frequency * sampling_frequency;
float sampling_period = 1.0f / sampling_frequency;
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
Eigen::Vector3f color = { 0,0,0 };
Eigen::Vector3f point = { j * 1.0f,i * 1.0f,0 };
for (int m = 0; m < sampling_frequency; m++) {
for (int n = 0; n < sampling_frequency; n++) {
int depth_buf_x, depth_buf_y;
depth_buf_x = j * Freq + n;
depth_buf_y = i * Freq + m;
color += temp_frame_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)];
}
}
color /= sampling_times;
set_pixel(point, color);
}
}
}
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
int sampling_frequency, sampling_times;
sampling_frequency = Freq;
sampling_times = sampling_frequency * sampling_frequency;
float sampling_period = 1.0f / sampling_frequency;
int minX = width, minY = height, maxX = 0, maxY = 0;
for (auto vert : v) {
if (vert.x() < minX)
minX = vert.x();
if (vert.y() < minY)
minY = vert.y();
if (vert.x() > maxX)
maxX = vert.x();
if (vert.y() > maxY)
maxY = vert.y();
}
Vector3f color = t.getColor();
for (int i = minY; i < maxY; i++) {
for (int j = minX; j < maxX; j++) {
float blend_rate;
int sample_counter = 0;
for (int m = 0; m < sampling_frequency; m++) {
for (int n = 0; n < sampling_frequency; n++) {
float x = j + (n + 0.5f) * sampling_period;
float y = i + (m + 0.5f) * sampling_period;
if (insideTriangle(x, y, t.v)) {
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
int depth_buf_x, depth_buf_y;
depth_buf_x = j * Freq + n;
depth_buf_y = i * Freq + m;
if (z_interpolated < depth_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)]) {
depth_buf[get_depth_buf_index(depth_buf_x, depth_buf_y)] = z_interpolated;
Vector3f temp_point = { depth_buf_x * 1.0f,depth_buf_y * 1.0f,0.0f };
Vector3f color = t.getColor();
set_temp_pixel(temp_point, color);
}
}
}
}
}
}
}
//下方有些函数做了部分修改
int rst::rasterizer::get_depth_buf_index(int x,int y) {
return (height*Freq-1-y)*width*Freq+x;
}
void rst::rasterizer::set_temp_pixel(const Eigen::Vector3f& point, const Eigen::Vector3f& color) {
auto ind = (height*Freq - 1 - point.y()) * width*Freq + point.x();
temp_frame_buf[ind] = color;
}
void rst::rasterizer::clear(rst::Buffers buff) {
if ((buff & rst::Buffers::Color) == rst::Buffers::Color) {
std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{ 0, 0, 0 });
}
if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth) {
std::fill(depth_buf.begin(), depth_buf.end(), std::numeric_limits<float>::infinity());
}
std::fill(temp_frame_buf.begin(), temp_frame_buf.end(), Eigen::Vector3f{ 0, 0, 0 });
}
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h) {
frame_buf.resize(w * h);
temp_frame_buf.resize(w * h * Freq * Freq);
depth_buf.resize(w * h*Freq*Freq);
}
ssaa的效果还是很不错的,但是不知道为什么在采样率为8x8,16x16时会产生灰色的图像,难道是因为精度或者是内存过大吗?下面依次是1,2,4,8,16倍采样。





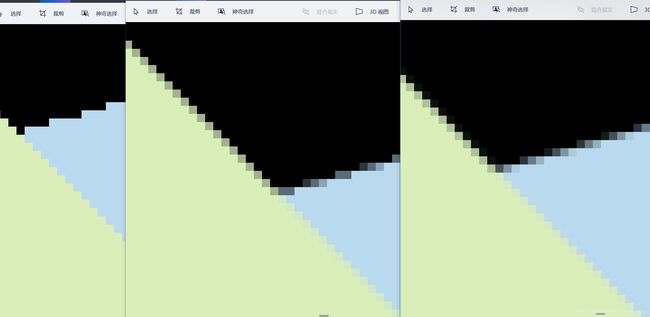
总结
MSAA
这块花了两天多的时间才搞出了比较理想的结果,性能上肯定是比ssaa高不少,这里的msaa只用了扩展的深度缓存空间,而ssaa还需要一个临时扩展帧缓冲,一番计算后再对这个缓冲做下采样。
下面有一些参考的文章,msaa的效果似乎都不是很好,也许msaa本来就很麻烦吧。
SSAA
ssaa的实现比较简单,比msaa容易实现的多了,但不知道是哪里出了问题导致高采样率的时候会出现异常图像。反走样的效果也很不错,不会出现msaa中的蜜汁“灰黑线”。缺点当然是显然易见了,需要大量的存储空间和计算时间。
最后
算是对这两种反走样方法有了一定的认识,两者在绘制图像时流程有着区别,在细节的地方各有各的区别,时间空间的消耗也相差很大。
参考
深入剖析MSAA
GAMES101学习笔记 作业2,作业3
GAMES101-现代计算机图形学学习笔记(作业02)
Games101-现代图形学入门-实验2
GAMES101-现代计算机图形学学习笔记(3)作业2

