【动手学习深度学习】循环神经网络-3.语言模型
上一篇:【动手学习深度学习】循环神经网络-2.文本预处理
文章目录
-
- 3.语言模型
-
- 3.1 学习语言模型
- 3.2 马尔科夫模型与n元语法
- 3.3 自然语言统计
- 3.4 随机采样与顺序分区
3.语言模型
- 给定文本序列 x 1 , . . . , x T x_1,...,x_T x1,...,xT,语言模型的目标是估计联合概率 p ( x 1 , . . . , x T ) p(x_1,...,x_T) p(x1,...,xT)
- 他的应用包括
- 做预训练模型(eg BERT, GPT-3)
- 生成文本,给定前面几个词,不断的使用 x t ∼ p ( x t ∣ x t − 1 , . . . , x 1 ) x_t \sim p(x_t|x_{t-1},...,x_1) xt∼p(xt∣xt−1,...,x1)来生成后续文本
- 判断多个序列中哪个更为常见,例如,短语“to recognize speech”和“to wreck a nice beach”读音上听起来非常相似。 这种相似性会导致语音识别中的歧义,但是这很容易通过语言模型来解决, 因为第二句的语义很奇怪。
3.1 学习语言模型
语言模型是如何对一个文档, 甚至是一个词元序列进行建模。 假设在单词级别对文本数据进行词元化,则概率为
P ( x 1 , . . . , x T ) = ∏ t = 1 T P ( x t ∣ x 1 , . . . , x t − 1 ) P(x_1,...,x_T)=\quad \prod_{t=1}^T P(x_t|x_1,...,x_{t-1}) P(x1,...,xT)=t=1∏TP(xt∣x1,...,xt−1)
例如,包含了四个单词的一个文本序列的概率是:
P ( d e e p , l e a r n i n g , i s , f u n ) = P ( d e e p ) P ( l e a r n i n g ∣ d e e p ) P ( i s ∣ d e e p , l e a r n i n g ) P ( f u n ∣ d e e p , l e a r n i n g , i s ) P(deep,learning, is, fun)=P(deep)P(learning|deep)P(is|deep,learning)P(fun|deep,learning,is) P(deep,learning,is,fun)=P(deep)P(learning∣deep)P(is∣deep,learning)P(fun∣deep,learning,is)
为了训练语言模型,我们需要计算单词的概率, 以及给定前面几个单词后出现某个单词的条件概率。 这些概率本质上就是语言模型的参数。训练数据集中词的概率可以根据给定词的相对词频来计算。 例如,可以将估计值 P ^ ( d e e p ) \hat{P}(deep) P^(deep)计算为任何以单词“deep”开头的句子的概率。 一种(稍稍不太精确的)方法是统计单词“deep”在数据集中的出现次数, 然后将其除以整个语料库中的单词总数。 这种方法效果不错,特别是对于频繁出现的单词。
使用计数来建模
- 假设序列长度为2,我们预测
p ( x , x ′ ) = p ( x ) p ( x ′ ∣ x ) = n ( x ) n n ( x , x ′ ) n ( x ) p(x,x^{'})=p(x)p(x^{'}|x)=\frac{n(x)}{n} \frac{n(x,x^{'})}{n(x)} p(x,x′)=p(x)p(x′∣x)=nn(x)n(x)n(x,x′)- 这里n是总词数, n ( x ) n(x) n(x), n ( x , n ′ ) n(x,n^{'}) n(x,n′)是单个单词和连续单词对出现的次数
- 比如
p ( d e e p , l e a r n i n g ) = p ( d e e p ) ∣ p ( l e a r n i n g ∣ d e e p ) = n ( d e e p ) n n ( d e e p , l e a r n i n g ) n ( d e e p ) p(deep,learning)=p(deep)|p(learning|deep)=\frac{n(deep)}{n} \frac{n(deep,learning)}{n(deep)} p(deep,learning)=p(deep)∣p(learning∣deep)=nn(deep)n(deep)n(deep,learning)
3.2 马尔科夫模型与n元语法
一元语法:令马尔科夫假设的 τ \tau τ等于0,每次算一个 x x x出现的概率,而不用考虑以前的状态对当前状态的影响。假设我们算一个长为4的序列,使用一元语法时,基本认为每个词是独立的。
p ( x 1 , x 2 , x 3 , x 4 ) = p ( x 1 ) p ( x 2 ) p ( x 3 ) p ( x 4 ) = n ( x 1 ) n n ( x 2 ) n n ( x 3 ) n n ( x 4 ) n p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2)p(x_3)p(x_4) = \frac{n(x_1)}{n} \frac{n(x_2)}{n} \frac{n(x_3)}{n} \frac{n(x_4)}{n} p(x1,x2,x3,x4)=p(x1)p(x2)p(x3)p(x4)=nn(x1)nn(x2)nn(x3)nn(x4)
二元语法:令马尔科夫假设的 τ \tau τ等于1,当前状态需要考虑前一个状态造成的影响。其中 n ( x 1 , x 2 ) n(x_1,x_2) n(x1,x2)代表 x 1 , x 2 x_1,x_2 x1,x2词元连续出现的次数。
p ( x 1 , x 2 , x 3 , x 4 ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 2 ) p ( x 4 ∣ x 3 ) = n ( x 1 ) n n ( x 1 , x 2 ) n ( x 1 ) n ( x 2 , x 3 ) n ( x 2 ) n ( x 3 , x 4 ) n ( x 3 ) p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2|x_1)p(x_3|x_2)p(x_4|x_3) = \frac{n(x_1)}{n} \frac{n(x_1,x_2)}{n(x_1)} \frac{n(x_2,x_3)}{n(x_2)} \frac{n(x_3,x_4)}{n(x_3)} p(x1,x2,x3,x4)=p(x1)p(x2∣x1)p(x3∣x2)p(x4∣x3)=nn(x1)n(x1)n(x1,x2)n(x2)n(x2,x3)n(x3)n(x3,x4)
三元语法:令马尔科夫假设的 τ \tau τ等于2,当前状态需要考虑前两个状态造成的影响。
p ( x 1 , x 2 , x 3 , x 4 ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 1 , x 2 ) p ( x 4 ∣ x 2 , x 3 ) p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)p(x_4|x_2,x_3) p(x1,x2,x3,x4)=p(x1)p(x2∣x1)p(x3∣x1,x2)p(x4∣x2,x3)
训练复杂度O(t)
3.3 自然语言统计
根据上一篇的时光机器数据集构建词表,并打印前10个最常用的(频率最高的)单词。
!pip install d2l==0.14
import random
import torch
from d2l import torch as d2l
# read_time_machine()等函数内容在上一节
tokens = d2l.tokenize(d2l.read_time_machine())
# 因为每个文本行不一定是一个句子或一个段落,因此我们把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]
[('e', 17838),
('t', 13515),
('a', 11704),
('i', 10138),
('n', 9917),
('o', 9758),
('s', 8486),
('h', 8257),
('r', 7674),
('d', 6337)]
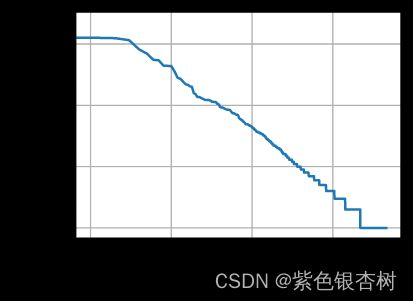
正如我们所看到的,最流行的词看起来很无聊, 这些词通常被称为停用词(stop words),因此可以被过滤掉。 尽管如此,它们本身仍然是有意义的,我们仍然会在模型中使用它们。如果使用一元语法直接预测,很难预测正确的结果。为了更好地理解,我们可以画出的词频图:
freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',xscale='log', yscale='log')
使用二元语法对词元进行组合
# 每连续两个词元组合成一个元组
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]
[(('of', 'the'), 309),
(('in', 'the'), 169),
(('i', 'had'), 130),
(('i', 'was'), 112),
(('and', 'the'), 109),
(('the', 'time'), 102),
(('it', 'was'), 99),
(('to', 'the'), 85),
(('as', 'i'), 78),
(('of', 'a'), 73)]
这里值得注意:在十个最频繁的词对中,有九个是由两个停用词组成的, 只有一个与“the time”有关。 我们再进一步看看三元语法的频率是否表现出相同的行为方式。
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]
[(('the', 'time', 'traveller'), 59),
(('the', 'time', 'machine'), 30),
(('the', 'medical', 'man'), 24),
(('it', 'seemed', 'to'), 16),
(('it', 'was', 'a'), 15),
(('here', 'and', 'there'), 15),
(('seemed', 'to', 'me'), 14),
(('i', 'did', 'not'), 14),
(('i', 'saw', 'the'), 13),
(('i', 'began', 'to'), 13)]
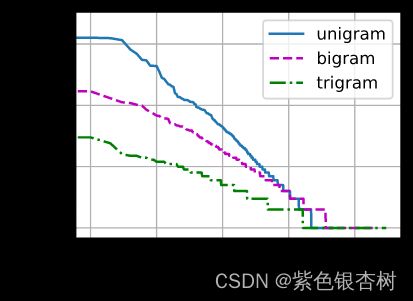
最后,我们直观地对比三种模型中的词元频率:一元语法、二元语法和三元语法。
bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',ylabel='frequency: n(x)', xscale='log', yscale='log',
legend=['unigram', 'bigram', 'trigram'])
3.4 随机采样与顺序分区
def seq_data_iter_random(corpus, batch_size, num_steps):
""" 使用随机抽样生成一个小批量子序列:
随机地生成一个小批量数据的特征和标签以供读取。在随机采样中每个样本都是在原始的长序列上任意捕获的子序列
corpus: 数字下标(词元对应的数字)
batch_size: 批量大小
num_steps: 马尔科夫假设的tau
"""
# 从随机偏移量开始对序列进行分区,随机范围包括num_steps-1
corpus = corpus[random.randint(0, num_steps - 1):]
# 减去1,是因为我们需要考虑标签
num_subseqs = (len(corpus) - 1) // num_steps
# 长度为num_steps的子序列的起始索引
initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
# 在随机抽样的迭代过程中,
# 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
random.shuffle(initial_indices)
def data(pos):
# 返回从pos位置开始的长度为num_steps的序列
return corpus[pos: pos + num_steps]
num_batches = num_subseqs // batch_size
for i in range(0, batch_size * num_batches, batch_size):
# 在这里,initial_indices包含子序列的随机起始索引
initial_indices_per_batch = initial_indices[i: i + batch_size]
X = [data(j) for j in initial_indices_per_batch] # 数据
Y = [data(j + 1) for j in initial_indices_per_batch] # 标签
yield torch.tensor(X), torch.tensor(Y)
def seq_data_iter_sequential(corpus, batch_size, num_steps):
"""使用顺序分区生成一个小批量子序列"""
# 从随机偏移量开始划分序列
offset = random.randint(0, num_steps)
num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
Xs = torch.tensor(corpus[offset: offset + num_tokens])
Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
num_batches = Xs.shape[1] // num_steps
for i in range(0, num_steps * num_batches, num_steps):
X = Xs[:, i: i + num_steps]
Y = Ys[:, i: i + num_steps]
yield X, Y
class SeqDataLoader:
"""加载序列数据的迭代器
use_random: 是否使用随机采样
max_tokens: 最大的token长度
"""
def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
if use_random_iter:
self.data_iter_fn = d2l.seq_data_iter_random
else:
self.data_iter_fn = d2l.seq_data_iter_sequential
self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
self.batch_size, self.num_steps = batch_size, num_steps
def __iter__(self):
return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)
def load_data_time_machine(batch_size, num_steps,
use_random_iter=False, max_tokens=10000):
"""返回时光机器数据集的迭代器和词表"""
data_iter = SeqDataLoader(
batch_size, num_steps, use_random_iter, max_tokens)
# 返回数据迭代器和词汇表
return data_iter, data_iter.vocab
随机采样
my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
print('X: ', X, '\nY:', Y)
X: tensor([[5, 6, 7, 8, 9],
[0, 1, 2, 3, 4]])
Y: tensor([[ 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5]])
X: tensor([[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
Y: tensor([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]])
X: tensor([[25, 26, 27, 28, 29],
[20, 21, 22, 23, 24]])
Y: tensor([[26, 27, 28, 29, 30],
[21, 22, 23, 24, 25]])
当特征为5,6时标签为7;当特征为6,7,8时,8对应的Y中的9,即标签是9;