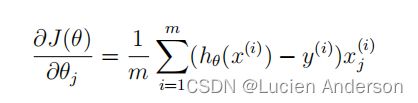超详细解析——吴恩达机器学习第三周作业Logistic Regression（逻辑回归）（Python实现）

---

一、Logistic Regression

1.1 Visualizing the data

在开始实现任何学习算法之前，如果可能的话，可视化数据总是很好的。在ex2.m的第一部分中，代码将加载数据，并通过调用函数plotData来显示在二维图上。现在您将在plotData中完成代码，以便它显示像图1这样的图形，其中轴是两个考试分数，正面和消极的例子用不同的标记显示。

data.describe()

观察这一系列数据的范围、大小、波动趋势等等，为后面的模型选择打下基础。

统计值变量说明：

count：数量统计，此列共有多少有效值
mean：均值
std：标准差
min：最小值
25%：四分之一分位数
50%：二分之一分位数
75%：四分之三分位数
max：最大值

然后创建散点图，分别用红蓝色的点代表是否通过

positive = data[data['admitted'].isin([1])]  # 1 
negetive = data[data['admitted'].isin([0])]  # 0
fig, ax = plt.subplots(figsize=(6,5)) # 设置图例的长宽
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
ax.scatter(negetive['exam1'], negetive['exam2'], c='r', marker='x', label='Not Admitted')
# 设置图例显示在图的上方
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width , box.height* 0.8])
ax.legend(loc='center left', bbox_to_anchor=(0.2, 1.12),ncol=2)
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

函数说明：

1. pandas.isin()：用来清洗数据，过滤某些行。data[‘admitted’].isin([1])表示筛选出数据标签admitted中值为1的数据
2. ax.scatter()：绘制散点。详细解释如下

前两项表示每个点的x,y轴数据值。
c代表散点的颜色。 常用的颜色字符串为b（blue，蓝色）、c（cyan，品红）、g（green，绿色）、k（black，黑色）、m（magenta，红色）、w（white，白色）、y（yellow，黄色）
label标记每种散点的标签名称。
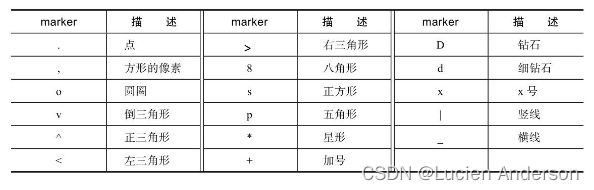
marker代表散点样式,下图是marker所代表的样式含义。

3. set_position()：用于设置轴在整个画布中的位置长度。前面两个表示原图坐标长度，后面表示新图坐标长度。
4. legend()：在图上标明一个图例，用于说明每条曲线的文字显示。

loc：图例位置，可取(‘best’, ‘upper right’, ‘upper left’, ‘lower left’, ‘lower right’, ‘right’, ‘center left’, ‘center , right’, ‘lower center’, ‘upper center’, ‘center’) ；若是使用了bbox_to_anchor，则这项就无效了
bbox_to_anchor：(横向看右，纵向看下),如果要自定义图例位置或者将图例画在坐标外边，用它，比如bbox_to_anchor=(1.4,0.8)，这个一般配合着ax.get_position()，set_position([box.x0, box.y0, box.width*0.8 , box.height])使用
ncol：图例的列数代码中表示图例显示有两列，默认为1

5. set_xlabel：设置x轴坐标名称，set_ylabel同理。

1.2 Implementation

1.2.1 Sigmoid Function

在你开始使用实际的成本函数之前，回想一下，逻辑回归假设的定义为：


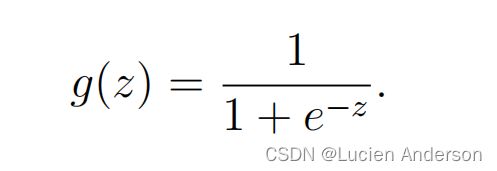
首先第一步是先在python中实现这个函数。这样它就可以被程序的其余部分调用

def sigmoid(z):
    return 1 / (1 + np.exp(- z))#np.exp()函数是求e^x的值的函数

简单测试一下

#np.arange()函数返回一个有终点和起点的固定步长的排列
#如x1表示为-10为起点，10终点，0.1为步长。其中步长支持小数。x1=[-10,-9.9……10]
x1 = np.arange(-10, 10, 0.1)
plt.plot(x1, sigmoid(x1), c='r')
plt.show()

1.2.2 Cost function and gradient

现在你将实现逻辑回归的成本函数和梯度，完成成本函数中的代码，以返回成本和梯度。
Cost function：


请注意，虽然这个梯度看起来与线性回归梯度相同，但这个公式实际上是不同的，因为线性回归和逻辑回归对hθ(x)有不同的定义。

def cost(theta, X, y):
    first = (-y) * np.log(sigmoid(X @ theta))#其中@表示矩阵乘法
    second = (1 - y)*np.log(1 - sigmoid(X @ theta))
    return np.mean(first - second)

现在，做一些设置，获取我们的训练集数据。

data.insert(0, 'Ones', 1)#增加一个列标签，方便后面操作。
#iloc：前面的冒号就是取行数，后面的冒号是取列数。
#冒号左右分别表示开始和结束位置遵循左闭右开原则
X = data.iloc[:, :-1].values #[:, :-1]表示除了最后一列的全部
y = data.iloc[:, -1].values #[:, -1]表示要取的列是从最后一列
theta = np.zeros(X.shape[1])#返回     一个与X列数相同的用0填充的数组

上面代码第一句为什么要增加一列全为1的列呢？

X₀假设为1，为了求出h(x)所以加了一列数据1

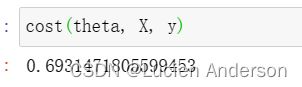
cost(theta, X, y)

gradient：

def gradient(theta, X, y):
    return (X.T @ (sigmoid(X @ theta) - y))/len(X)  

1.2.3 Learning parameters using fminunc

在前面的作业中，我们通过实现梯度下降找到了线性回归模型的最优参数。编写了一个成本函数并计算了它的梯度，然后相应地采取了一个梯度下降步骤。下面我们要对θ进行学习。由于我们使用Python，我们可以用SciPy的“optimize”命名空间来做事情。
只需传入cost函数，已经所求的变量theta，和梯度。cost函数定义变量时变量tehta要放在第一个，若cost函数只返回cost，则设置fprime=gradient。

import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
result

fmin_tnc()使用参数讲解
func：优化的目标函数
x0：初值
fprime：提供优化函数func的梯度函数，不然优化函数func必须返回函数值和梯度，或者设置approx_grad=True
args：元组，是传递给优化函数的参数

1.2.4 Evaluating logistic regression

在学习参数之后，我们可以使用模型来预测特定学生是否会被录取。
接下来，我们要编写一个函数，用我们所学的参数theta来为数据集X输出预测。

x1 = np.arange(130, step=0.1)
x2 = -(final_theta[0] + x1*final_theta[1]) / final_theta[2]

#此类函数详细解释上文已有，故不在赘述
fig, ax = plt.subplots(figsize=(8,5))
ax.scatter(positive['exam1'], positive['exam2'], c='b', label='Admitted')
ax.scatter(negetive['exam1'], negetive['exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x1, x2)
ax.set_xlim(0, 130)
ax.set_ylim(0, 130)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_title('Decision Boundary')
plt.show()

二、Regularized logistic regression

在这部分的练习中，我们将实施正则化的逻辑回归来预测来自制造工厂的微芯片是否通过了质量保证（QA）。在质量保证期间，每个微芯片都要经过各种测试，以确保其能够正常工作.
假设您是该工厂的产品经理，并且您有两种不同测试中的一些微芯片的测试结果。从这两个测试中，您希望确定微芯片是应该被接受还是被拒绝。为了帮助您做出决定，您有一个关于过去微芯片的测试结果的数据集，从中您可以建立一个逻辑回归模型。

2.1 Visualizing the data

首先进行数据可视化

data2 = pd.read_csv('E:\python work\ex2data2.txt', names=['Test 1', 'Test 2', 'Accepted'])
data2.head()

def plot_data():
    positive = data2[data2['Accepted'].isin([1])]
    negative = data2[data2['Accepted'].isin([0])]

    fig, ax = plt.subplots(figsize=(8,5))
    ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
    ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
    ax.legend()
    ax.set_xlabel('Test 1 Score')
    ax.set_ylabel('Test 2 Score')
    
plot_data()

我们的数据集不能通过图中的直线分为正的和负的例子。因此，一个直接的逻辑回归的应用将不会在这个数据集上表现得很好，因为逻辑回归将只能找到一个线性的决策边界。

2.2 Feature mapping

如果样本量多，逻辑回归问题很复杂，而原始特征只有x1,x2可以用多项式创建更多的特征。因为更多的特征进行逻辑回归时，得到的分割线可以是任意高阶函数的形状。为更好地匹配数据我们从每个数据点创建更多的特性，我们将把这些特征映射到x1和x2的所有多项式项中，直到六次幂。

def feature_mapping(x1, x2, power):
    data = {}
    for i in np.arange(power + 1):#power+1为终点,起点取默认值0，步长取默认值1
        for p in np.arange(i + 1):
            data["f{}{}".format(i - p, p)] = np.power(x1, i - p) * np.power(x2, p)#np.power()用于求数组元素的n次方
    return pd.DataFrame(data)

x1 = data2['Test 1'].values#将属性以返回给定DataFrame的numpy表示形式
x2 = data2['Test 2'].values
_data2 = feature_mapping(x1, x2, power=6)
_data2.head()

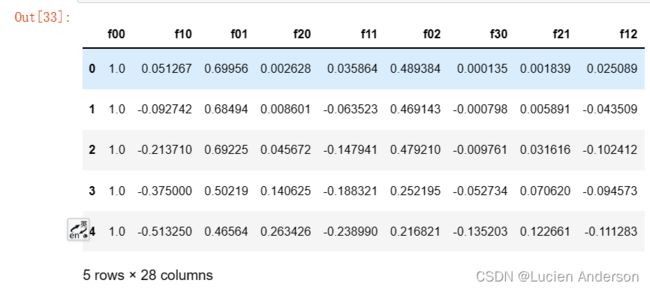
由于这个映射，我们的两个特征的向量已经被转换为一个28维的向量。在这个高维特征向量上训练的逻辑回归分类器将有一个更复杂的决策边界，当在我们的二维图中绘制时将出现非线性函数图像。
虽然特征映射允许我们构建一个更准确的分类器，但它也更容易受到过拟合的影响。在练习的下一部分中，我们将实现正则化逻辑回归来拟合数据，并自己看看正则化如何帮助解决过拟合问题。

2.3 Cost function and gradient

现在，您将实现代码来计算的成本函数和梯度的正则化逻辑回归。完成成本功能注册表中的代码，以返回成本和梯度。回想一下，逻辑回归中的正则化成本函数是

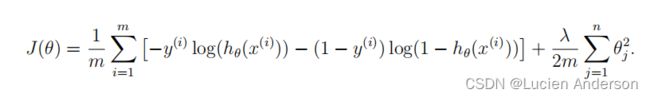
# 这里因为做特征映射的时候已经添加了偏置项，所以不用手动添加了。
X = _data2.values
y = data2['Accepted'].values
theta = np.zeros(X.shape[1])
X.shape, y.shape, theta.shape  

def costReg(theta, X, y, l=1):
    _theta = theta[1: ]#不惩罚第一项
    reg = (l / (2 * len(X))) *(_theta @ _theta)
    return cost(theta, X, y) + reg

costReg(theta, X, y, l=1)  

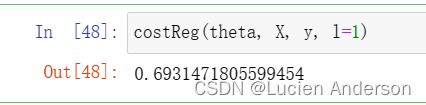
因为我们未对是θ₀进行正则化，所以梯度下降算法将分两种情形

对上面的算法中 j=1,2,…,n 时的更新式子进行调整可得：

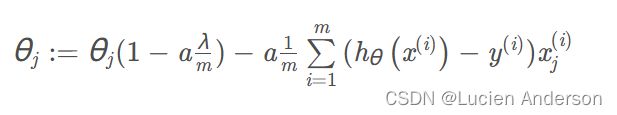
同样不惩罚第一个θ

def gradientReg(theta, X, y, l=1):
    reg = (1 / len(X)) * theta
    reg[0] = 0  
    return gradient(theta, X, y) + reg

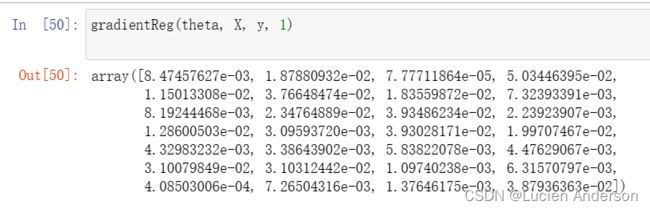
gradientReg(theta, X, y, 1)

确定θ参数：

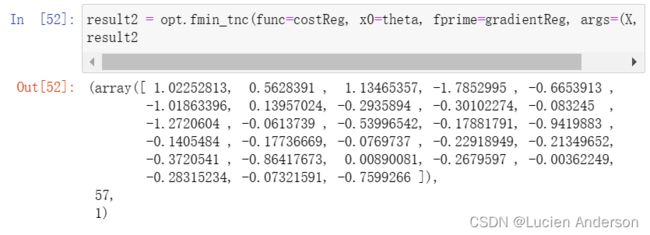
result2 = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, y, 2))
result2

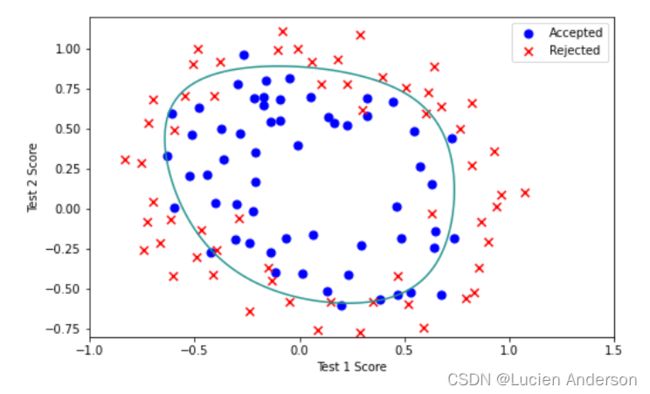
2.4 Plotting the decision boundary

x = np.linspace(-1, 1.5, 250)#表示在-1到1.5之间均匀生成250个点
xx, yy = np.meshgrid(x, x)#生成网格点坐标矩阵
final_theta = result2[0]#θ值
#ravel()方法将数组维度拉成一维数组
#feature_mapping特征映射
z = feature_mapping(xx.ravel(), yy.ravel(), 6).values
z = z @ final_theta
z = z.reshape(xx.shape)#在不更改数据的情况下为数组赋予xx的形状

plot_data()
plt.contour(xx, yy, z,0)#绘制等高线，表示指定z中XY轴坐标为xx，yy
plt.ylim(-.8, 1.2)#确定y轴坐标范围从-0.8--1.2

至此全部结束！