SVM损失函数和softmax损失函数

  对于线性模型，包括神经网络，损失函数是衡量模型输出和真实值的标准。在训练过程中，损失函数越小，表明我们的模型在训练集上越好的拟合数据。在优化模型的过程中，我们一般会采用一些优化方法，如梯度下降法，去最小化损失函数。而损失函数一般是数据和模型参数的函数，即$L_i=f(X_i,W)$,这里的$i$表示某一个样本的损失函数，$X_i=({\mathbf{x}}_{\mathbf{i}},y_i)$表示该样本的特征以及标签。总的损失函数为$L=\frac{1}{m}\sum L_i$，由于$X=\{({\mathbf{x}}_{\mathbf{i}},y_i){\}}_{i=1}^m$的分布在训练过程中是固定的，所以我们只需最小化$L$就可得到模型的参数$W$。
  在前面的文章中我们已经在逻辑回归在多分类问题中的应用
，介绍了逻辑回归的损失函数，这个损失函数实际上可以通过极大似然估计推倒，也可以理解为逻辑回归预测的概率分布和真实概率分布的交叉熵。在那篇文章中，由于逻辑回归一般只能运用于二分类问题，所以采用了$One$ $vs$ $All$的策略，即对于每一个类都训练一个分类器。训练过程中，一个类作为正例，其余类作为反例。
在这篇文章中，我们直接介绍两个针对多分类的损失函数：SVM损失函数和Softmax损失函数。

SVM损失函数

为了说明SVM损失函数的意义，我们以线性分类为例。假设我们有一个$m$个d维样本，即样本矩阵$X\in {\mathbb{R}}^{m\times d}$。我们用权重矩$W\in {\mathbb{R}}^{d\times c}$，其中$c$为类别数。我们将两个矩阵相乘。得到一个分数矩阵$S\in {\mathbb{R}}^{m\times c}$，这个矩阵第$i$行第$j$列表示第$i$个样本在第$j个$类别的分数。分数越高表示模型预测第$i$个样本越可能属于第$j$个类别。
SVM损失函数的想法在于：对于单个样本$\{({\mathbf{x}}_{\mathbf{i}}，y_i)\}$，其属于第$y_i$个类别。其真实类别所对应的分数为$S_{i{y}_i}$。如果这个样本除$y_i$以外的其他类别$j(j=1,2,...,m;j\ne y_i)$的分数$S_{ij}$和此样本真实类别的分数$S_{i{y}_i}$足够接近，我们就认为模型并不足以辨别样本$i$属于$y_i$还是$j$。此时样本$i$则在$j$类别上产生损失。我们再将样本$i$在所有类别上的损失进行求和，得到样本$i$的损失。于是有：
$$L_i=\sum _{j\ne y_i}\max (S_{ij}-S_{i{y}_i}+\Delta ，0)$$
从上式可以看出，当$S_{ij}-S_{i{y}_i}+\Delta <0$时，求和部分为0，即$S_{i{y}_i}-S_{ij}>\Delta$。此式表明如果模型给出关于样本$i$正确分类分数比错误分类分数至少大于一个$\Delta$值时，我们认为模型可以辨别样本是$y_i$类别还是$i$类别，此时样本在$i$类别上不产生损失，所以为0。反之，则认为模型对${\mathbf{x}}_{\mathbf{i}}$不可分辨样本是$y_i$类别还是$i$类别。
   而间隔$\Delta$的取值一般并不重要，这是由于一般我们我只关注分数矩阵中$S$那个类别的分数最大，对于类别的绝对值并不关注，即我们只关注相对值。比如$S=XW$和$S=X(2W)$,得到的分数最大的类别是不变的。所以$W$和$2W$两个权重矩阵是等效的。假设我们将间隔设为$\Delta$，我们要最小化$S_{ij}-S_{i{y}_i}+\Delta$,即${\mathbf{x}}_{\mathbf{i}}{\mathbf{w}}_{\mathbf{j}}^{\mathbf{T}}-{\mathbf{x}}_{\mathbf{i}}{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{\mathbf{T}}+\Delta$,其中$x_i$表示$X$的第$i$行，$w_j$和$w_{y_i}$为$W$的$i$列和第$y_i$列。但是如果我们将间隔改为$2\Delta$,那么有${\mathbf{x}}_{\mathbf{i}}{\mathbf{w}}_{\mathbf{j}}^{{}^{\prime }\mathbf{T}}-{\mathbf{x}}_{\mathbf{i}}{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{{}^{\prime }\mathbf{T}}+2\Delta$,显然${\mathbf{w}}_{\mathbf{j}}^{{}^{\prime }}=2{\mathbf{w}}_{\mathbf{j}}$。因为这两个优化问题实际上是解决一个问题，只有${\mathbf{w}}_{\mathbf{j}}^{{}^{\prime }}=2{\mathbf{w}}_{\mathbf{j}}$，此时对于后一个优化问题${\mathbf{x}}_{\mathbf{i}}{\mathbf{w}}_{\mathbf{j}}^{{}^{\prime }\mathbf{T}}-{\mathbf{x}}_{\mathbf{i}}{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{{}^{\prime }\mathbf{T}}+2\Delta ={\mathbf{x}}_{\mathbf{i}}2{\mathbf{w}}_{\mathbf{j}}^{\mathbf{T}}-{\mathbf{x}}_{\mathbf{i}}2{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{\mathbf{T}}+2\Delta$，才与间隔为$\Delta$的优化问题是等效的。而我们也已经提过$W$和$2W$对于线性分类是等效的。所以$\Delta$的取值并不重要。简而言之，$\Delta$的取值改变只会让$W$等比例的改变，而$W$和$\alpha W$对于线性分类是等效的，所以$\Delta$并不重要。一般我们取1。下面为计算SVM损失函数和损失函数梯度的代码：

import numpy as np

def svm_loss_naive(W, X, y, regularization_param):  #W:dimension * num_class
    num_training = X.shape[0]
    num_class = W.shape[1]
    score = X @ W
    
    Loss = 0
    for i in range(num_training):
        for j in range(num_class):
            if j == y[i]:
                continue
            Loss += max(0,score[i,j]-score[i,y[i]]+1)
    Loss_reg = Loss / num_training + regularization_param * np.sum(W * W)
    
    dW = 0
    for i in range(num_training):
        for j in range(num_class):
            dW_for_i_j = np.zeros(W.shape)
            if j==y[i] or score[i,j]-score[i,y[i]]+1 < 0:
                continue
            dW_for_i_j[:,j] = X[i]
            dW_for_i_j[:,y[i]] = -X[i]
            dW += dW_for_i_j
    dW = dW / num_training + 2 * regularization_param * W
    
    return Loss_reg,dW

  关于梯度的计算，总的损失函数为$L=\frac{1}{m}{\sum }_i{L}_i=\frac{1}{m}{\sum }_i{\sum }_{j\ne y_i}\max (S_{ij}-S_{i{y}_i}+\Delta ，0)$。所以我们可以遍历所有的样本$i$和属性$j$,对于每一对$(i,j)$求梯度，最后相加除以$m$。对于那些score[i,j]-score[i,y[i]]+1 < 0项不需要考虑，因为损失为常数，那么梯度为全是0的矩阵，对于j==y[i]的项也不考虑，因为求和符号中并没有考虑$j=y_i$的情况。对于$S_{ij}-S_{i{y}_i}+\Delta >0$的项，第一项会在W矩阵的第j列产生一个$x_i$的列向量，而后一项会在$y_i$列产生一个$-x_i$的列向量，最后一项为常数项，不考虑。
  上面的代码需要两个遍历过程，下面是将这个计算过程矩阵化的结果，矩阵化之后，就省去了遍历，使得运行速度更快。代码如下：

def svm_loss_vectorized(W,X,y,regularization_param):
    
    num_training = X.shape[0]
    num_class = W.shape[1]
    score = X @ W
    diff_matrix = score - score[range(num_training),y].reshape((num_training,1)) + 1
    diff_matrix = diff_matrix * (diff_matrix > 0)
    diff_matrix[range(num_training),y] = 0
    Loss = np.sum(diff_matrix)
    Loss_reg = Loss/num_training + regularization_param * np.sum(W*W)
    
    indication_matrix = (diff_matrix>0)
    dW_1 = X.T @ indication_matrix
    
    y_matrix = np.zeros((num_training,num_class))
    y_matrix[range(num_training),y] = 1
    index_non_minus_per_i = np.sum(indication_matrix,axis=1) #每个样本中对类别求和的不为0元素的个数
    M = index_non_minus_per_i.reshape((num_training,1)) * y_matrix #指示了每个样本求和中需要求和的项以及求和次数
    dW_2 = X.T @ M
    
    dW = dW_1 - dW_2
    dW = dW / num_training + 2*regularization_param*W
    
    return Loss_reg , dW

  对于求损失,diff_matrix的第$i$行和第$j$列为给出了$S_{ij}-S_{i{y}_i}+\Delta$，那么我们只要将diff_matrix中应当为0的项设为0，然后对这个矩阵中所有元素求和即可（不考虑正则化）。这里我们将所有小于0的项设为0，将$j=y_i$的项设为0，设为0，再求和。
  对于梯度，上面已经说明$L$的的中求和符号中的某一项$S_{ij}-S_{i{y}_i}+\Delta$对梯度的贡献为只有两列不为0，$j$列为${\mathbf{x}}_{\mathbf{i}}$，$y_i$列为$-{\mathbf{x}}_{\mathbf{i}}$。我们在将这些项相加。所以我们只要统计梯度矩阵中每一列中具有$x_i$成分的数量。
  对于求梯度的第一项的正号部分，indication_matrix用于统计diff_matrix不为0的项，这样我们就能知道损失函数的求和符号中的项哪些不为0。dW_1 = X.T @ indication_matrix算出了损失函数第一项的梯度。
  对于梯度第二项的负号部分：y_matrix则是一个$m\times c$维的矩阵，如果一个样本$i$的真实标记为$j$,则这个矩阵的第$i$行第$j$列为1，其余为0。所以只有$(i,y_i)$的项为1。我们再indication_matrix按行求和，这样我们就得到了一个$m$维的向量index_non_minus_per_i，这个向量表示每个样本损失函数$L_i$对于$j$求和中不为0的项的个数。将这个向量按列和y_matrix相乘得到矩阵M，矩阵M标识了每个样本$i$中第二项的需要求和项个数，这里只有$(i,y_i)$不为0，比如M的第$i$行第$y_i$列为$k$,则样本${\mathbf{x}}_{\mathbf{i}}$在梯度矩阵的$y_i$列的求和次数为$k$。于是有dW_2 = X.T @ M就得到梯度的负号成分。
将以上两个成分相减，就得到了梯度。
以上过程，我们都忽略了正则化项。

Softmax损失函数

  损失函数是基于Softmax函数的损失函数。softmax函数的形式为$f_j(z)=\frac{e^{z_j}}{\sum e^{z_k}}$，它的作用是将一组数组$[z_1,z_2,...,z_m]$,压到0到1的范围。softmax函数为单调函数，所以$z_j$越大，所对应的softmax函数越大。由于softmax函数的范围0到1，而且一组数的softmax函数的和为1，所以我们可以认为其将数组变为概率的形式。
  结合到线性分类上，假设我们对于样本${\mathbf{x}}_{\mathbf{i}}$得到$c$个类别的分数，我们利用softmax函数就能将分数变为概率的形式，比如$f_j(x_i)=\frac{e^{{\mathbf{w}}_{\mathbf{j}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}{{\sum }_k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}$表示样本${\mathbf{x}}_{\mathbf{i}}$属于$j$的概率。于是我们就得到了样本${\mathbf{x}}_{\mathbf{i}}$属于每一个类别的概率$[f_1(x_i),f_2(x_i),...,f_c(x_i)]$,即我们得到了模型预测的一组概率分布。
  关于Softmax函数的导出，具有两种解释：一种是我们只要让${\mathbf{x}}_{\mathbf{i}}$属于正例的概率越大越好，即让$f_j(x_i)=\frac{e^{{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}{{\sum }_k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}$的概率越大越好，那么也就是让$-\log (\frac{e^{{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}{{\sum }_k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}})$越小越好。
  另一种解释则更为严谨：从上面可以看出，我们通过模型和softmax函数得到了样本${\mathbf{x}}_{\mathbf{i}}$属于每个$[f_1(x_i),f_2(x_i),...,f_c(x_i)]$类别的概率，而我们通过${\mathbf{x}}_{\mathbf{i}}$的真实标记得到的真实概率为$[0,...,1,...0]$,这里的1为位于第$y_i$位。显然我们希望模型预测的概率和实际概率越相近越好，此时我们就可以用交叉熵来表示两个概率分布的相近的程度。$p(x)$和$q(x)$的交叉熵表达式为$H(p,q)=-{\sum }_{x}p(x)log(q(x))$。它的值越小表示$p(x)$和$q(x)$越相近。于是我们我们就可以将损失函数表示为两个分布交叉熵，即$L_i=-\log (\frac{e^{{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}{{\sum }_k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}})$。或者
$$L_i=-\log (\frac{e^{{\mathbf{w}}_{{\mathbf{y}}_{\mathbf{i}}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}{{\sum }_k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}})=-w_{y_i}^T{x}_i+log\sum _k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}$$
这就是样本$x_i$的softmax损失函数的表达式。进一步得到总的损失函数：
$$L=\frac{1}{m}\sum _i{L}_i$$。
而对于$L_i$关于$w_{ij}$的梯度为：
$$\frac{\partial L_i}{\partial w_{dj}}=-\mathbb{I}(j=y_i)+\frac{x_{id}{e}^{{\mathbf{w}}_{\mathbf{j}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}{{\sum }_k{e}^{{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}}}$$。
关于softmax损失函数的代码如下：

import numpy as np

def softmax_loss_naive(W,X,y,reg_param):
    num_tr = X.shape[0]
    dim, num_class = W.shape
    
    total_loss = 0
    for i in range(num_tr):
        exp_score_for_i = 0
        for j in range(num_class):
            score_i_for_class_j = W[:,j] @ X[i]
            exp_score_i_for_class_j = np.exp(score_i_for_class_j)
            exp_score_for_i += exp_score_i_for_class_j
        loss_i = -W[:,y[i]] @ X[i] + np.log(exp_score_for_i)
        total_loss += loss_i
    loss = total_loss / num_tr + reg_param * np.sum(W * W)
    
    grad = 0
    for i in range(num_tr):
        first_term = np.zeros(W.shape)
        score_for_i = W.T @ X[i]
        log_sum = np.sum(np.exp(score_for_i))
        log_score_for_i = np.exp(score_for_i)
        second_term = X[i].reshape((dim,1)) @ log_score_for_i.reshape((1,num_class)) / log_sum
        first_term[:,y[i]] = - X[i]
        grad_for_i = first_term + second_term
        grad += grad_for_i
    grad = grad / num_tr + 2 * reg_param * W
    
    return loss,grad

同样给出矩阵化的代码：

def softmax_loss_vectorized(W,X,y,reg_param):
    num_tr = X.shape[0]
    dim, num_class = W.shape
    
    score = X @ W
    exp_score = np.exp(score)
    exp_score_for_each_sample = np.sum(exp_score,axis=1)
    
    log_score = np.log(exp_score_for_each_sample)
    second_term = np.sum(log_score)
    first_term = np.sum(score[range(num_tr),y])
    loss = - first_term + second_term
    loss = loss / num_tr + reg_param * np.sum(W*W)
    
    y_matrix = np.zeros(score.shape)
    y_matrix[range(num_tr),y] = 1
    first_term_grad = X.T / exp_score_for_each_sample.reshape((1,num_tr)) @ exp_score
    second_term_grad = - X.T @ y_matrix
    grad = first_term_grad + second_term_grad
    grad = grad / num_tr + 2 * reg_param * W
    
    return loss,grad

应用

我们将上述两个损失函数利用于CIFAR-10数据集。我们首先写一个父类LinearClassifiers，这个父类包含训练和预测方法，这两个部分实际上和损失函数的选取无关。我们在为两个损失函数写两个类SVMLinearClassifier和SoftmaxLinearClassifier，继承了上述父类，但是其中的损失函数不同。下面为代码：

import numpy as np
from .svm_loss import svm_loss_vectorized
from .softmax_loss import softmax_loss_vectorized

class LinearClassifiers():
    def __init__(self):
        self.W = None

    def train(self,X,y,reg_param=1e-5,learning_rate=1e-3,\
              batch_size=200,num_iters=100,verbose=False):
        
        num_training,dimension = X.shape
        num_class = np.max(y) + 1
        
        if self.W == None:
            self.W = np.random.randn(dimension,num_class)*0.001
            
        loss_history = []
        for i in range(num_iters):
            batch_index = np.random.choice(num_training,batch_size,\
                                           replace=False)
            X_batch = X[batch_index]
            y_batch = y[batch_index]
            loss,grad = self.loss(X_batch,y_batch,reg_param)
            loss_history.append(loss)
            self.W -= learning_rate * grad
            if verbose and i % 10 == 0:
                print('The loss of %d is %f' % (i,loss))
            
        return loss_history
        
    def predict(self,X_test):
        score = X_test @ self.W
        y_test = np.argmax(score,axis=1)
        return y_test
        
    def loss(self,X,y,reg_param):
        pass
        

class SVMLinearClassifier(LinearClassifiers):
    
    def loss(self,X,y,reg_param):
        return svm_loss_vectorized(self.W,X,y,reg_param)

class SoftmaxLinearClassifier(LinearClassifiers):
    
    def loss(self,X,y,reg_param):
        return softmax_loss_vectorized(self.W,X,y,reg_param)

  这里需要注意的是我们在train方法中使用了随机梯度下降法，其中的verbose表示是否在训练过程中打印损失。下面我们分别使用线性模型，利用这两个损失函数对CIFAR图片数据集进行分类。
  CIFAR是一个简单的图片集，它是由分辨率为32×32×3的图片组成的数据集，也就是说数据集每个样本的特征维度为32×32×3=3072维。而数据的类别数为10。数据集的训练集大小为50000，测试大小为10000。首先是读取数据，并处理：

###Split data to get train,validation,test,development
from cs231n.data_utils import load_CIFAR10
import numpy as np
import matplotlib.pyplot as plt

###Get data
X_train_all,y_train_all,X_test_all,y_test_all = load_CIFAR10\
    ('cs231n/datasets/cifar-10-batches-py')

num_train = 49000
num_val = 1000
num_test = 1000

mask_train = range(num_train)
X_train = X_train_all[mask_train]
y_train = y_train_all[mask_train]

mask_val = range(num_train,num_train+num_val)
X_val = X_train_all[mask_val]
y_val = y_train_all[mask_val]

mask_test = range(num_test)
X_test = X_test_all[mask_test]
y_test = y_test_all[mask_test]

### Reshape the data to make it available for training.
X_train = X_train.reshape((num_train,-1))
X_val = X_val.reshape((num_val,-1))
X_test = X_test.reshape((num_test,-1))
X_dev = X_dev.reshape((num_dev,-1))

###Preprocessing the data (mean subtracting and add one column).
mean_data = np.mean(X_train,axis=0)
mean_image = mean_data.reshape((32,32,3))
X_train -= mean_data
X_val -= mean_data
X_test -= mean_data

X_train = np.hstack((X_train,np.ones((num_train,1))))
X_val = np.hstack((X_val,np.ones((num_val,1))))
X_test = np.hstack((X_test,np.ones((num_test,1))))

  这里我们取训练集中50000个样本中的1000个样本作为单独的验证集，以选取参数。而测试集我们也只用了1000个样本。由于数据集中的样本以图片形式存在，所以我么首先要将其拉平以转化为特征向量。接着我们将向量中心化，这里我们并没有在除以方差向量以实现标准化，这是由于：图片中像素一般为0—255，所以每个特征范围较为固定，并没有量纲的区别，所以不需要在除以方差向量。我们在将训练集，验证集，以及特征集的最后一列加上全为1的列向量，这样我们在训练和预测过程中就不需要在加上偏置，偏置直接存在于权重矩阵中。下面我们任意选取一组参数（学习率learning_rate、正则化常数reg_param、迭代次数num_iters），首先看看svm损失函数在线性模型上的效果如何，这里我们打印了训练过程中的损失。：

import classifiers_set
svm_linear_classifier = classifiers_set.SVMLinearClassifier()
time0 = time.time()
loss_history = svm_linear_classifier.train\
    (X_train,y_train,learning_rate=1e-7,reg_param=2.5e4,num_iters=1500,verbose=True)
time1 = time.time()
print('It took %f s' % (time1 - time0))

###Results on training set and validation set.
y_pre_on_train = svm_linear_classifier.predict(X_train)
accuracy_train = np.sum(y_pre_on_train == y_train) / y_train.shape[0]
print('The accuracy in training set is %f' % accuracy_train)
y_pre_on_val = svm_linear_classifier.predict(X_val)
accuracy_val = np.sum(y_pre_on_val == y_val) / y_val.shape[0]
print('The accuracy in validation set is %f' % accuracy_val)

得到：

The loss of 0 is 799.278216
The loss of 10 is 721.951307
The loss of 20 is 648.994895
The loss of 30 is 585.725589
The loss of 40 is 531.324861
The loss of 50 is 477.622664
The loss of 60 is 433.915647
The loss of 70 is 392.429319
The loss of 80 is 354.816596
The loss of 90 is 319.258982
The loss of 100 is 292.095450
The loss of 110 is 263.190338
The loss of 120 is 238.929221
The loss of 130 is 215.452137
The loss of 140 is 195.085179
The loss of 150 is 178.408341
The loss of 160 is 160.964610
The loss of 170 is 146.337298
The loss of 180 is 132.254647
The loss of 190 is 120.903493
The loss of 200 is 109.401802
The loss of 210 is 99.131151
The loss of 220 is 89.731525
The loss of 230 is 81.794346
The loss of 240 is 74.546828
The loss of 250 is 67.316442
The loss of 260 is 61.072373
The loss of 270 is 56.474009
The loss of 280 is 51.010107
The loss of 290 is 47.104181
The loss of 300 is 43.379602
The loss of 310 is 39.374820
The loss of 320 is 36.528839
The loss of 330 is 33.062526
The loss of 340 is 30.035705
The loss of 350 is 28.720728
The loss of 360 is 25.860836
The loss of 370 is 23.885473
The loss of 380 is 22.286930
The loss of 390 is 20.648929
The loss of 400 is 18.666645
The loss of 410 is 17.521825
The loss of 420 is 16.530333
The loss of 430 is 15.773515
The loss of 440 is 14.541040
The loss of 450 is 13.181780
The loss of 460 is 12.960236
The loss of 470 is 11.897264
The loss of 480 is 11.265084
The loss of 490 is 10.891549
The loss of 500 is 10.999159
The loss of 510 is 9.544070
The loss of 520 is 9.294225
The loss of 530 is 9.459192
The loss of 540 is 9.499533
The loss of 550 is 8.397499
The loss of 560 is 7.796843
The loss of 570 is 7.710667
The loss of 580 is 7.714568
The loss of 590 is 7.397773
The loss of 600 is 7.436262
The loss of 610 is 7.313390
The loss of 620 is 6.415401
The loss of 630 is 6.642724
The loss of 640 is 6.785695
The loss of 650 is 6.613267
The loss of 660 is 6.744118
The loss of 670 is 6.227589
The loss of 680 is 5.861897
The loss of 690 is 6.316749
The loss of 700 is 5.895940
The loss of 710 is 6.499795
The loss of 720 is 5.843577
The loss of 730 is 5.935666
The loss of 740 is 5.766207
The loss of 750 is 5.659979
The loss of 760 is 6.065064
The loss of 770 is 5.618366
The loss of 780 is 6.188924
The loss of 790 is 5.622487
The loss of 800 is 5.606496
The loss of 810 is 5.682202
The loss of 820 is 5.756562
The loss of 830 is 5.527888
The loss of 840 is 5.821458
The loss of 850 is 5.318783
The loss of 860 is 5.810715
The loss of 870 is 5.516746
The loss of 880 is 5.602206
The loss of 890 is 5.423054
The loss of 900 is 5.202074
The loss of 910 is 5.777529
The loss of 920 is 5.503457
The loss of 930 is 5.558496
The loss of 940 is 5.440331
The loss of 950 is 6.048546
The loss of 960 is 4.806574
The loss of 970 is 5.614158
The loss of 980 is 5.396602
The loss of 990 is 5.155151
The loss of 1000 is 5.197775
The loss of 1010 is 4.580944
The loss of 1020 is 5.442690
The loss of 1030 is 5.178101
The loss of 1040 is 5.056695
The loss of 1050 is 5.152060
The loss of 1060 is 5.582913
The loss of 1070 is 5.503516
The loss of 1080 is 5.019396
The loss of 1090 is 5.314748
The loss of 1100 is 5.268996
The loss of 1110 is 4.813873
The loss of 1120 is 4.939847
The loss of 1130 is 4.952678
The loss of 1140 is 5.629128
The loss of 1150 is 5.376255
The loss of 1160 is 5.114201
The loss of 1170 is 5.403888
The loss of 1180 is 5.691718
The loss of 1190 is 4.888743
The loss of 1200 is 5.095463
The loss of 1210 is 5.679937
The loss of 1220 is 5.425218
The loss of 1230 is 5.554016
The loss of 1240 is 5.809155
The loss of 1250 is 5.482086
The loss of 1260 is 5.030008
The loss of 1270 is 5.179006
The loss of 1280 is 5.044685
The loss of 1290 is 5.495019
The loss of 1300 is 5.038069
The loss of 1310 is 5.100689
The loss of 1320 is 5.528823
The loss of 1330 is 5.228730
The loss of 1340 is 5.275179
The loss of 1350 is 5.691322
The loss of 1360 is 4.995985
The loss of 1370 is 5.430789
The loss of 1380 is 5.618861
The loss of 1390 is 5.573897
The loss of 1400 is 5.330611
The loss of 1410 is 5.025699
The loss of 1420 is 5.575841
The loss of 1430 is 5.047263
The loss of 1440 is 5.432847
The loss of 1450 is 5.893019
The loss of 1460 is 5.142476
The loss of 1470 is 5.100369
The loss of 1480 is 5.710984
The loss of 1490 is 5.332315
It took 6.493972 s

将损失可视化，看是否收敛：

###Visualize the variation with iters.
plt.plot(loss_history)
plt.xlabel('Number of iterations')
plt.ylabel('Loss')
plt.show()

得到

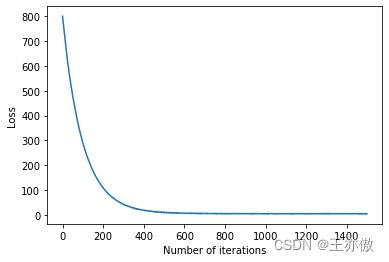
我们可以看到损失最后已经趋于平缓，已经收敛。最后得到训练集和验证集上的准确率：

###Results on training set and validation set.
y_pre_on_train = svm_linear_classifier.predict(X_train)
accuracy_train = np.sum(y_pre_on_train == y_train) / y_train.shape[0]
print('The accuracy in training set is %f' % accuracy_train)
y_pre_on_val = svm_linear_classifier.predict(X_val)
accuracy_val = np.sum(y_pre_on_val == y_val) / y_val.shape[0]
print('The accuracy in validation set is %f' % accuracy_val)

结果为：

The accuracy in training set is 0.369367
The accuracy in validation set is 0.385000

最后我们在验证集上的准确率为0.385左右，由于线性分类模型较为简单，所以0.385的准确率并不高，但是明显好于随机猜测。下面我们通过验证集选取更好的参数，从而得到更好的模型：

###Choose the combination of the parameters.
best_calssifier = None
best_val_accuracy=0
results={}

learning_rates=[5e-8,1e-7,5e-7,1e-6,5e-6,1e-5,5e-5,1e-4]
reg_params = [1e3,5e3,1e4,5e4,1e5,5e5]
for learning_rate in learning_rates:
    for reg_param in reg_params:
        classifier = classifiers_set.SVMLinearClassifier()
        classifier.train(X_train,y_train,learning_rate=learning_rate,\
                         reg_param=reg_param,num_iters=1500)
        y_pre_on_val = classifier.predict(X_val)
        y_pre_on_train = classifier.predict(X_train)
        accuracy_val = np.sum(y_pre_on_val == y_val) / y_val.shape[0]
        accuracy_train = np.sum(y_pre_on_train==y_train) / y_train.shape[0]
        if accuracy_val>best_val_accuracy:
            best_classifier = classifier
            best_val_accuracy = accuracy_val
            best_lr = learning_rate
            best_rp = reg_param
        results[(learning_rate,reg_param)] = (accuracy_val,accuracy_train)

将得到的模型用于测试集，并检查最佳参数：

1e-07 10000.0
The accuracy in test set is 0.371000

也就是说在学习率为1e-07，正则化常数为10000.0得到其在验证集上的准确率越高，而这组参数下的模型在测试集上的准确率为0.371000。

下面为softmax的结果：

###Use validation set to tune the hyperparameters.
import cs231n.classifiers.classifiers_set as classifiers_set
best_val_accuracy = 0
best_classifier = None
results = {}

learning_rates=[5e-8,1e-7,5e-7,1e-6,5e-6,1e-5,5e-5,1e-4]
reg_params = [1e3,5e3,1e4,5e4,1e5,5e5]
print(X_val.shape,X_tr.shape)
for lr in learning_rates:
    for rp in reg_params:
        Classifier = classifiers_set.SoftmaxLinearClassifier()
        Classifier.train(X_tr,y_tr,reg_param=rp,learning_rate=lr,num_iters=1500)
        y_pre_on_val = Classifier.predict(X_val)
        y_pre_on_tr = Classifier.predict(X_tr)
        accuracy_val = np.sum(y_pre_on_val == y_val) / y_val.shape[0]
        accuracy_tr = np.sum(y_pre_on_tr == y_tr) / y_tr.shape[0]
        if accuracy_val > best_val_accuracy:
            best_classifier = Classifier
            best_val_accuracy = accuracy_val
            best_rp = rp
            best_lr = lr
        results[(lr,rp)] = (accuracy_val,accuracy_tr)
       
####Give accuracy of test set.
y_pre_on_test = best_classifier.predict(X_test)
accuracy_test = np.sum(y_pre_on_test==y_test) / y_test.shape[0]
print(best_rp,best_lr)
print('The accuracy of test set is %f' % accuracy_test)

得到：

1000.0 1e-06
The accuracy of test set is 0.395000

我们看到利用softmax损失函数的线性分类模型和SVM损失函数的线性模型相比而言，较好。

总结

我们可以看到将 图片的每个像素作为一个特征维度，然后利用线性模型分类并不好。这是由于图片的像素本身作为特征具有局限性，它实际上忽略了图片中像素和像素之间的联系。所以对于图片的分类问题，或者说对于视觉问题，现在较为先进的方法为卷积神经网络。