R语言机器学习篇——逻辑回归2(多分类)
在多分类的问题中，同样可用逻辑回归进行预测，这里的一些概念便不做过多介绍，重点说明参数的意义。
多分类回归参数意义
如果响应变量y分为k类，则多项逻辑模型有k-1个参数向量
，假设将第一类作为参照类别，这里对参数的解释可采取如下思路
对于响应变量y归属于第k类的条件概率与属于第一类的条件概率之比为：
这就是事件属于第k类与属于第1类发生几率之比，也称为相对风险。
进一步讨论，如果某特征变量为离散变量（如性别、职业），则可通过几率比来解释变量对y的作用，假设该变量增加一单位，从
,记上面条件概率的新值为
、
，则可计算新几率与原几率的比率，即为“几率比”，也称为相对风险比率（RRR）:
因此若参数为0.12时，几率比为1.13，这意味着参数增加一单位时，相对于参照方案，新几率变为原几率的1.13倍，
案例介绍
使用R包mlbench中的Glass数据集，此数据的响应变量Type包括6种玻璃的类别，为了法医学的目的，有时需要根据玻璃碎片折射率以及不同化学元素含量，预测犯罪现场的玻璃类别，因此特征变量包括RI(折射率）以及8种不同元素在相应氧化物中的重量占比，该数据集共有214个观测值，1个响应变量以及9个特征变量，最后呈现的部分数据如下所示
library(mlbench)
data(Glass)
head(Glass) #展示数据前六行
运用对应的图像查看响应变量以及部分特征变量的关系，如下图所示
#条形图、箱线图
par(mfrow=c(1,2))
plot(Glass$Type,xlab="Glass Type",ylab="count",main="Barplot")
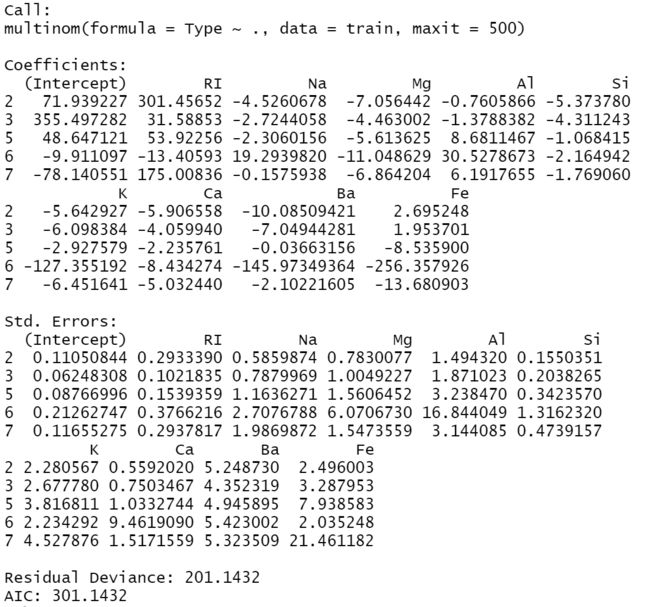
boxplot(Mg~Type,data=Glass,main="Mg Boxplot")
运用图像观察数据的大致特征之后，需要对数据集随机选取30%的数据作为测试集，剩下70%的作为训练集，并使用R的nnet包进行多项逻辑回归，其中函数multinom中的参数“maxit=500”表示最多迭代500次，默认值为100。在最终的输出结果为300次迭代后算法收敛，最后查看回归结果，如下：
#生成训练集、测试集
set.seed(1)
train_index<-sample(214,150)
train<-Glass[train_index,]
test<-Glass[-train_index,]
#多项逻辑回归
library(nnet)
fit<-multinom(Type~.,data=train,maxit=500) #maxit表示迭代次数
summary(fit) #查看回归结果
#几率比
exp(coef(fit))
回归结果展示了多项逻辑回归的系数（每个特征变量有5行回归系数，都是以第1类的响应变量为参照类别），相应的标准误，以及残差偏离度和AIC。接下来可查看几率比或相对风险比率
通过观察几率比的结果，可得出如下结论（以特征变量RI为例，它是一个数值型变量）：得到的5行几率比都以第一类响应变量为参考类别，当RI增加一单位时，则选择响应变量为2的几率为选择响应变量为1的8.334931e+130倍，同理选择响应变量为3的几率是选择1的5.232673e+13倍（待补充）
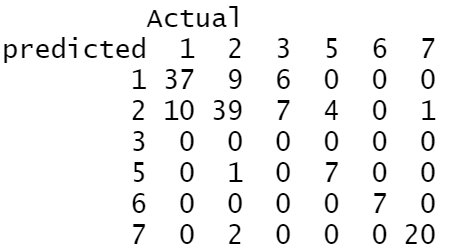
接下来运用训练集，查看训练误差，可得到预测的条件概率，也可直接预测得出响应变量的类别，这里用预测出的响应变量类别，得到混淆矩阵，再计算预测的准确率
#训练误差
prob_train<-predict(fit,type="probs") #参数表示预测条件概率
head(prob_train)
pred_train<-predict(fit,type="class") #class就是预测响应变量类别
head(pred_train)
table<-table(predicted=pred_train,Actual=train$Type) #混淆矩阵
table
Accuracy<-sum(diag(table))/sum(table) #准确率
#[1] 0.7333333
上图为训练集预测响应变量类别的混淆矩阵，由于行列数较多，因此在计算准确率时，用diag直接得出主对角线上的数字，再用sum进行求和，最后计算出准确率为0.733,。接下来再去考察测试集的误差，并计算出可衡量多分类逻辑模型预测效果的Kappa指数
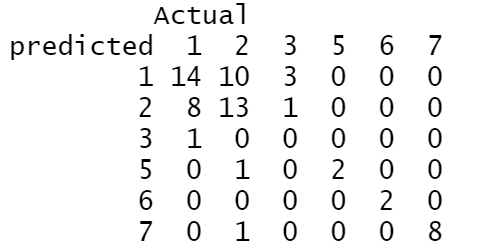
#测试误差
prob_test<-predict(fit,type="probs",newdata=test)
head(prob_test)
pred_test<-predict(fit,type="class",newdata=test)
head(pred_test)
table<-table(predicted=pred_test,Actual=test$Type)
table
Accuracy<-sum(diag(table))/sum(table)
#[1] 0.609375
#计算Kappa函数
library(vcd)
Kappa(table)
上图为测试集的混淆矩阵，根据它计算出的准确率为0.609，比训练集的低，这表示训练误差可能低估了真实的测试误差，虽然测试集的准确率较低，但由于是一个多分类问题，随机猜测是不现实的。
最后计算出Kappa指标，如下：
得出最后的指标为0.436，这意味着预测值与实际值之间具有中等一致性，说明预测效果一般。