《一个 Q-learning 算法的简明教程》之Python代码
- 本文是对A Painless Q-learning Tutorial (一个 Q-learning 算法的简明教程)中的强化学习教程做的Python代码实现
- 代码框架参考【莫烦Python】强化学习 Reinforcement Learning
场景简述
一栋房子,共6个房间(最外层也看做一个房间5),目标是快速地从某个房间走出(即走到房间5)
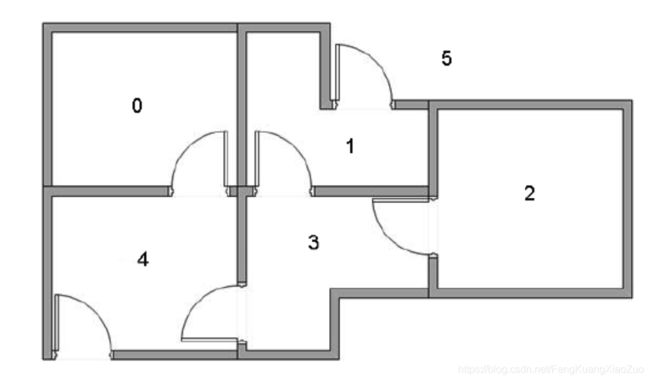
抽象为有向图,并设定奖赏(只有通向房间5的转移有奖赏100,其他情况都为0)。

代码实现
# -*- coding: utf-8 -*-
"""
Created on Wed Mar 3 14:13:13 2021
仿写一个走房间的Q-learning
@author: YI
"""
import networkx as nx
import numpy as np
import pandas as pd
import time
np.random.seed(2)
""" 状态:共6个状态(房间)
动作:通向哪个房间
"""
N_STATES = 6 ### 共6个房间
ACTIONS = list(range(N_STATES)) ### 可以通向那个房间
EPSILON = 0.9 ## epsilon-greedy parameter
DISCOUNT = 0.8 ## 折扣
LEARNING_RATE = 1 ## 学习率
MAX_EPISODES = 1000
def define_environment():
"""定义一个环境:确定哪些房间相连,以及奖赏"""
G = nx.DiGraph() # 创建有向图
G.add_edge(0,4,weight=0)
G.add_edge(1,3,weight=0)
G.add_edge(1,5,weight=100)
G.add_edge(2,3,weight=0)
G.add_edge(3,1,weight=0)
G.add_edge(3,2,weight=0)
G.add_edge(3,4,weight=0)
G.add_edge(4,0,weight=0)
G.add_edge(4,3,weight=0)
G.add_edge(4,5,weight=100)
G.add_edge(5,1,weight=0)
G.add_edge(5,4,weight=0)
G.add_edge(5,5,weight=100)
return G
def build_q_table(n_states, actions):
"""
建立一个初始的Q表 (DataFrame类型)
"""
table = pd.DataFrame(
np.zeros((n_states, len(actions))), #初始化
columns = actions,
)
return table
def choose_action(state, q_table, environment):
""" 选动作(根据当前的状态和Q表)
+++++++ 厄普西隆-greedy 策略 +++++++
"""
optional_actions = [k for k in environment[state]] ## 可选的动作
if np.random.rand()<EPSILON: # 选最好的
state_actions = q_table.loc[state,:][optional_actions] ## 挑出来可选的 状态-动作
state_actions = state_actions.reindex(np.random.permutation(state_actions.index)) # 打乱索引顺序,防止两者恰好相等时选不到第二个的情况
action = state_actions.idxmax() # 选Q值最大的动作
else: # 选随机动作
action = np.random.choice(optional_actions)
return action
def get_env_feedback(S,A):
""" 在某个状态S采取行动A后进入的下一个状态S_和获得的奖励R"""
### 下一个状态就是房间号(即动作A的编号),奖赏就是两个房间之间连边的权值
return A, environment.get_edge_data(S,A)['weight']
def use_q_table(S, q_table):
""" 完成训练后,用Q表选动作
"""
actions = [S] ### 表示走过的房间
is_terminated = False
while not is_terminated:
state_actions = q_table.iloc[S,:] ## 子表:该状态下 各动作 对应的q值
A = state_actions.idxmax()
S_,R = get_env_feedback(S, A) # 进入下一个状态、获得状态转移带来的环境奖励
actions.append(S_)
if S_==5:
is_terminated = True
S = S_
return actions
if __name__=="__main__":
print('学习阶段...')
""" 强化学习主循环
"""
environment = define_environment()
q_table = build_q_table(N_STATES, ACTIONS)
for episode in range(MAX_EPISODES): # 总共玩MAX_EPISODES轮游戏
print('%d episodes:'%episode)
step_counter = 0
S = np.random.choice(list(range(N_STATES)))
is_terminated = False
while not is_terminated:
A = choose_action(S, q_table, environment)
S_,R = get_env_feedback(S, A) # 进入下一个状态、获得状态转移带来的环境奖励
q_current = q_table.iloc[S, A] # Q(s,a)的当前值
q_target = R + DISCOUNT * q_table.iloc[S_,:].max() # S1到S2获得的奖赏+S2状态下采取某动作可获得的最大Q
if S_ ==5: ### 目标房间的编号为5
is_terminated=True
q_table.iloc[S,A] += LEARNING_RATE * (q_target - q_current) # 更新:旧+学习率*差异
S = S_ # 进入到下一个状态
step_counter += 1
# print('--------')
# print(q_table)
# time.sleep(0.5)
"""应用阶段"""
print('最短路径:')
for s in list(range(N_STATES)):
actions = use_q_table(s, q_table)
print(actions)
按照A Painless Q-learning Tutorial (一个 Q-learning 算法的简明教程)中的设定:学习率为1,折扣为0.8,训练1000次得到的收敛结果与其相同。相应的Q表与最短路径为:
Q表
0 1 2 3 4 5
0 0.0 0.0 0.0 0.0 400.0 0.0
1 0.0 0.0 0.0 320.0 0.0 500.0
2 0.0 0.0 0.0 320.0 0.0 0.0
3 0.0 400.0 256.0 0.0 400.0 0.0
4 320.0 0.0 0.0 320.0 0.0 500.0
5 0.0 400.0 0.0 0.0 400.0 500.0
最短路径:
[0, 4, 5]
[1, 5]
[2, 3, 1, 5]
[3, 1, 5]
[4, 5]
[5, 5]