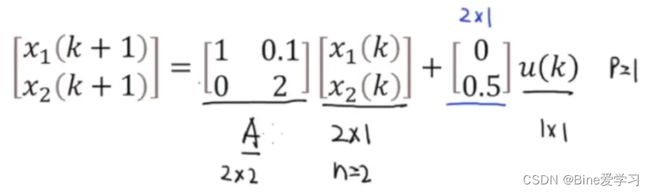控制算法-模型预测MPC
本文记录一下MPC控制算法的学习过程和自己的理解，初步接触控制算法，理解肯定不是很完善，重在记录思考的过程。
背景
随着自动驾驶技术以及机器人控制技术的不断发展及逐渐火热，模型预测控制(MPC)算法作为一种先进的控制算法，其应用范围与领域得到了进一步拓展与延伸。目前提出的模型预测控制算法主要有基于非参数模型的模型算法控制(MAC)和动态矩阵控制(DMC)，以及基于参数模型的广义预测控制(GPC)和广义预测几点配置控制(GPP)。【知乎拷的】主要是现在的自动驾驶会用到这个控制方法来做车的制动、油门、方向盘转角的控制，最近很火。
虽然模型预测控制算法的种类有多种，但始终离不开这三大要素：
- 预测模型——对未来一段时间内的输出进行预测；
- 滚动优化——滚动进行有限时域在线优化(最优控制)；
- 反馈校正——通过预测误差反馈，修正预测模型，提高预测精度
MPC控制算法
MPC的全称是模型预测控制（Model Predictive Control），简单来说就是利用一个现有模型来针对系统未来状态进行预测，同时决定应该采取什么样的动作能保证系统在接下来一段时间内的状态能与之前预测的相符合。
MPC如何工作？
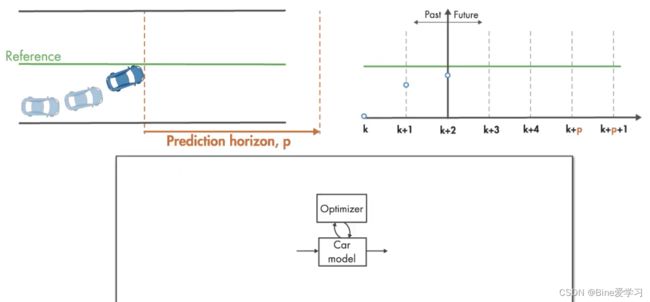
借B站视频的图说明一下过程。在车辆行驶的过程中，当上层给出了规划的路径（Reference Line），控制模块就需要控制车辆沿参考线走。从k时刻开始，MPC会预测接下来p时刻车的轨迹，使得车逼近目标轨迹。在到达k+1时刻时，MPC会再次预测接下来p时刻车的轨迹，再走一个时刻，再预测p时刻。不断的迭代，在不断的向前推进的时候不是没有目的的，而是通过最小化Cos Function，来知道逼近的过程。需要注意的是MPC会每个时刻预测接下来的p时刻，但是只会根据预测走一个时刻，在到达下一时刻会接着预测，这个也是在线优化需要较大性能的原因。
大概过程应该都清楚了。个人感觉和智能算法有类似的地方，有Function知道这前进的过程。下面就是，它咋做到如此的呢？：
MPC如何实现它的优化思想（工作过程）？
通过模型来预测系统在某一未来时间段内的表现来进行优化控制。多用于数位控制，系统模型通过离散状态空间表达X(k+1) = AX(k) + Bu(k) 。
如下图所示，k之前的是过去时刻（已知），k之后是未来时刻（未知）
MPC一般分为3步：
- 估计/测量当前系统的状态，也就是首先获取当前输入u(k-1)对应的输出y(k)。
- 基于最优控制策略得到的控制器输出u(k)，u(k+1)…，u(k+N-1)来进行最优化，对应的被控对象模型预测输出y(k+1)，y(k+2)…y(k+N)。
- 重要一步，在执行下一时刻控制时，只取u(k) 进行输入，然后回到step1进行滚动优化控制。
疑问：
控制器和被控对象是什么？
在自动驾驶中控制器就是MPC模型，系统就是无人车系统。
这里的J 为Cos_Function是什么意思？
上上图和下图的代价函数其实是一样的，E表示的是误差项，u表示的是输入项，矩阵相乘的形式方便运算。
举例来说，以两入两出系统为例，系统状态即为输出，参考值为0：
有了代价函数如何来做最优化呢？
最优化部分的数学推导，挺烦人的数学推导。有几种方法来做优化的，下面只是其中通过二次规划来做。
二次规划（Quadratic Programming）
对于二次规划来说，一般形式是这样的：
前面是二次型的，后面是线性的。如果Q写成对角矩阵的形式(对角矩阵除对角元素完全是0，对角元素可以看作权重系数)，那前面部分可以认为是求解最小二乘问题。（学过最小二乘，立个Flag下次写篇最小二乘复习一下）
对于二次规划的求解，可以通过MATLAB或Python完成。所以对于模型预测控制来说，需要将我们的模型化成上述一般形式，并进行求解计算。
将MPC模型化成二次规划形式
首先给出模型，以及在k时刻的预测控制量u(k)，即输入，以及对应的预测状态量x(k)，N为预测区间（Predictive Horizon）。
假设条件及代价函数（假设Q、R为对角阵）
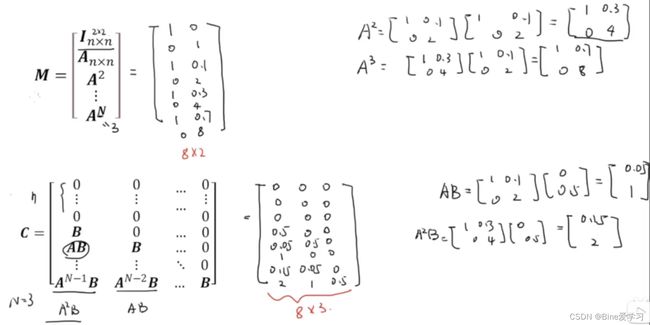
上述代价函数的输入包括当前时刻的x和u，而对比我们上面给出的二次规划中的一般形式（只有一个输入z）还不太一样，因此对上述代价函数进行改造。设系统在k时刻的初始状态为 X(k)（已知）。
将 X(k)（上面绿色）公式代入代价函数J中，可得：
这时的代价函数形式与上面给出的二次规划的形式就是一样的了，其中 是初始的测量值，不影响做最优化的部分。
以上就是通过完整的数学推导建立最优化的数学模型，有了这个模型之后，我们就可以利用该模型对这个系统进行优化以及模型预测控制设计。
对于一个状态空间模型来说，它的维度可以表示如下：
例如，给出一个二阶的单输入例子：
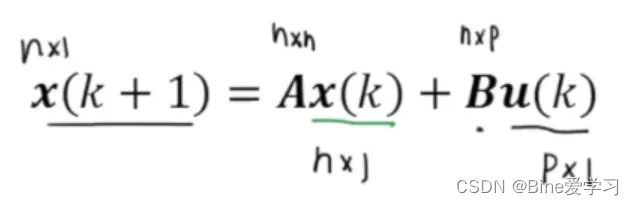
对于上一篇文章中涉及到的一些变量，它们的维度分别为：
假设A、B矩阵以及预测区间分别为：
带入到上面的公式中：
上次课我们总结了，对于代价函数J，可以转换成下面这种形式，只包括已知的k时刻的状态量x(k)以及输入向量U(k)：
参考链接
https://blog.csdn.net/zxxxxxxy/article/details/103700436
https://www.zhihu.com/people/xcalan9595/posts
下次学习Apollo在无人驾驶的MPC和PID控制。===>